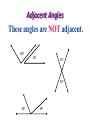* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Angle Pairs
Perspective (graphical) wikipedia , lookup
Technical drawing wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Rotation formalisms in three dimensions wikipedia , lookup
Line (geometry) wikipedia , lookup
Integer triangle wikipedia , lookup
History of trigonometry wikipedia , lookup
Perceived visual angle wikipedia , lookup
Multilateration wikipedia , lookup
Rational trigonometry wikipedia , lookup
Compass-and-straightedge construction wikipedia , lookup
Trigonometric functions wikipedia , lookup
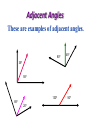
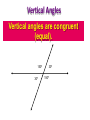
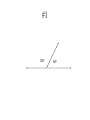
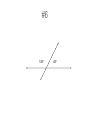
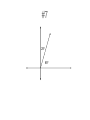
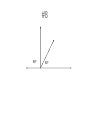
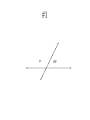
7-1 7-2 Angles PA Measurement of an Angle 2 To denote the measure of an angle we write an “m” in front of the symbol for the angle. Here are some common angles and their measurements. m1 45 1 m2 90 2 m3 135 3 4 m4 180 3 Congruent Angles • So, two angles are congruent if and only if they have the same measure. • So, The angles below are congruent. Means Congruent Means Equal A B if and only if mA mB. 4 Types of Angles • An acute angle is an angle that measures less than 90 degrees. • A right angle is an angle that measures exactly 90 degrees. • An obtuse angle is an angle that measures more than 90 degrees. acute right obtuse 5 Types of Angles • A straight angle is an angle that measures 180 degrees. (It is the same as a line.) • When drawing a right angle we often mark its opening as in the picture below. right angle straight angle 6 Perpendicular Lines • Two lines are perpendicular if they intersect to form a right angle. See the diagram. • Suppose angle 2 is the right angle. Then since angles 1 and 2 are supplementary, angle 1 is a right angle too. Similarly, angles 3 and 4 are right angles. • So, perpendicular lines intersect to form four right angles. 2 1 3 4 7 Perpendicular Lines • The symbol for perpendicularity is . • So, if lines m and n are perpendicular, then we write m n. m mn n Adjacent Angles Adjacent angles share a common vertex and one common side. Adjacent angles are “side by side” and share a common ray. 15º 45º Adjacent Angles These are examples of adjacent angles. 80º 45º 35º 55º 130º 85º 20º 50º Adjacent Angles These angles are NOT adjacent. 100º 50º 35º 35º 55º 45º Vertical Angles • Two angles formed by intersecting lines and have no sides in common but share a common vertex. • Are congruent. Common Vertex 75º When 2 lines intersect, they make vertical angles. 105º 105º 75º Vertical Angles Vertical angles are opposite one another. 75º 105º 105º 75º Vertical Angles Vertical angles are opposite one another. 75º 105º 105º 75º Vertical Angles Vertical angles are congruent (equal). 150º 30º 30º 150º Vertical Angles Two angles that are opposite angles. Vertical angles are congruent. Name the Vertical Angles 14 5 8, 1 23 3 5 7 4 6 8 2 67 Supplementary Angles Add up to 180º. 40º 120º 60º Adjacent and Supplementary Angles 140º Supplementary Angles • Two angles are supplementary if their measures add up to 180. • If two angles are supplementary each angle is the supplement of the other. • If two adjacent angles together form a straight angle as below, then they are supplementary. 1 2 1 and 2 are supplementary 18 Complementary Angles Add up to 90º. 20º 20º 70º Adjacent and Complementary Angles 70º Complementary Angles • Two angles are if their measures add upcomplementary to 90. • If two angles are complementary, then each angle is called the complement of the other. • If two adjacent angles together form a right angle as below, then they are complementary. 1 and 2 are complementary if ABC is a A 1 B 2 C right angle 20 Supplementary vs. Complementary How do I remember? The way I remember is this: • C comes before S in the alphabet. • 90 comes before 180 when I count. • Complementary is 90, Supplementary is 180. Guess Who? • I am an angle. Guess Who? • I am an angle. • I have 180° Guess Who? • I am an angle. • I have 180° • I look like this: Guess Who? • I am an angle. • I have 180° • I look like this: Supplementary Complementary Guess Who? • I am two adjacent angles. Guess Who? • I am two adjacent angles. • I look like an “L” with a line in the middle. Guess Who? • • • • I am two adjacent angles. I look like an “L” with a line in the middle. I add up to 90° I look like this: Guess Who? • • • • I am two adjacent angles. I look like an “L” with a line in the middle. I add up to 90° I look like this: Complementary Supplementary Guess Who? Complementary Supplementary Guess Who? Complementary Supplementary Review • Complementary angles are……. Review • Complementary angles are……. Review • Supplementary Angles are….. Practice Time! Find the missing angle I know that these angles are complementary. They must add up to 90° So…… 90 – 55 = 35 The missing angle is 35 55 x You try. Are they supplementary or complementary? x 20 Find the missing side. You try. Are they supplementary or complementary? complementary Find the missing side. x 20 90 – 20 = 70 The missing angle Is 70 One More 50 x Find the missing angle 120 I know these are supplementary angles. Supplementary angles add up to 180. The given angle is 120. So….. 180 – 120 = 60 The missing angle is 60 x Find the missing angle 130 What kind of angles? What’s the missing angle? x Find the missing angle 130 What kind of angles? Supplementary What’s the missing angle? Adds up to 180, so….. 180 – 130 = 50 x Find the missing angle x Do this one on your own. 30 Directions: Identify each pair of angles as adjacent, vertical, supplementary, complementary, or none of the above. #1 120º 60º #1 120º 60º Supplementary Angles Adjacent Angles #2 30º 60º #2 30º 60º Complementary Angles #3 75º 75º #3 Vertical Angles 75º 75º #4 40º 60º #4 40º 60º None of the above #5 60º 60º #5 60º 60º Vertical Angles #6 135º 45º #6 135º 45º Supplementary Angles Adjacent Angles #7 25º 65º #7 25º 65º Complementary Angles Adjacent Angles #8 90º 50º #8 90º 50º None of the above Directions: Determine the missing angle. #1 ?º 45º #1 135º 45º #2 ?º 65º #2 25º 65º #3 ?º 35º #3 35º 35º #4 ?º 50º #4 130º 50º #5 ?º 140º #5 140º 140º #6 ?º 40º #6 50º 40º Transversal • Definition: A line that intersects two or more lines in a plane at different points is called a transversal. • When a transversal t intersects line n and m, eight angles of the following types are formed: Exterior angles Interior angles Consecutive interior angles Alternative exterior angles Alternative interior angles Corresponding angles m n t Corresponding Angles Corresponding Angles: Two angles that occupy corresponding positions. The corresponding angles are the ones at the same location at each intersection 26 3 7 15 1 3 5 7 4 8 2 4 6 8 75 Angles and Parallel Lines • 1. 2. 3. If two parallel lines are cut by a transversal, then the following pairs of angles are congruent. Corresponding angles Alternate interior angles Alternate exterior angles Proving Lines Parallel • If two lines are cut by a transversal and corresponding angles are congruent, then the lines are parallel. A B C D Alternate Angles • Alternate Interior Angles: Two angles that lie between parallel lines on opposite sides of the transversal (but not a linear pair). 3 6, 4 5 • Alternate Exterior Angles: Two angles that lie outside parallel lines on opposite sides of the transversal. 2 7, 1 8 1 3 5 7 2 4 6 8 Lesson 2-4: Angles and Parallel Lines 78 Example: If line AB is parallel to line CD and s is parallel to t, find the measure of all the angles when m< 1 = 100°. Justify your answers. A 1 4 C 5 8 m<2=80° m<3=100° m<4=80° 2 12 3 6 10 11 B D 13 14 16 15 7 s 9 t m<5=100° m<6=80° m<7=100° m<8=80° m<9=100° m<10=80° m<11=100° m<12=80° m<13=100° m<14=80° m<15=100° m<16=80° Lesson 2-4: Angles and Parallel Lines 79 Proving Lines Parallel • If two lines are cut by a transversal and alternate interior angles are congruent, then the lines are parallel. A B C D Ways to Prove Two Lines Parallel • Show that corresponding angles are equal. • Show that alternative interior angles are equal. • In a plane, show that the lines are perpendicular to the same line. Homework Pg 305 #6-14e, 18-32e (just answers) Pg 309 #6-24e (just answers)