Download PHYS 536 Active Filters Introduction The Low Pass

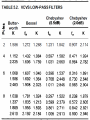
PHYS 536
Active Filters
Introduction
Active filters provide a sudden change in signal amplitude for a small change
in frequency. Several filters can be used in series to increase the attenuation
outside the break frequency. High pass, low pass, band pass, Butterworth, and
Chebyshev filters are investigated in this experiment.
Two methods of filter design are considered:
• Convenient time-constants are selected. Then the closed-loop gain (G0 )
is adjusted to obtain the desired frequency response.
• The closed-loop gain is selected, and then the time constants are adjusted
to obtain the desired frequency response.
The Low Pass Filter
The low pass circuit is shown in Fig. 1.
Figure 1: The low pass filter
The closed loop gain for this circuit is
1
G0 =
R3 + R4
R4
(1)
Gain Adjustment Method for the Low Pass Filter
To obtain the required component values, set R1 = R2 and C1 = C2 . Next,
select a convenient capacitor value. The resistor is then calculated to obtain the
desired break frequency. This value is given by
R1 =
1
2πfn fc C1
(2)
Next, R4 is selected for convenience and R3 is calculated to adjust G0 to the
value needed to obtain the desired frequency response (i.e. Bessel, Butterworth,
Chebyshev, etc.).
R3 = R4 (G0 − 1)
(3)
G0 and fn are obtained from the table of parameters given at the end of the lab
instructions. In this table, G0 is labeled K. For a Butterworth filter, fn = 1.
Multistage Filters
Better filter performance can be obtained by including more R-C attenuators.
(Each RC attenuator contributes one “pole” to the filter.) Only two RC attenuators can be used with one op-amp, hence better filters have several op amps
in series. For example, an 8-pole filter would use 4 op amps. The individual
op amps in the filter do not have the same frequency response as a 2-pole filter
of the same type, as shown by the parameters given in the table at the end of
the lab. Each op amp in a multistage filter has a different frequency response,
but their combined effect is closer to an ideal filter, i.e. no attenuation below
the break and no gain above the break. The gain expression for a multistage
Butterworth filter is
G = G0
2n
f
fc
(4)
+1
where n is the number of poles in the total filter.
The gain is approximately
constant (G = G0 ) below the break frequency (fc ),
f
because the term fc is very small when n is large and f < fc . The same term
makes the gain decrease rapidly when f > fc .
2
Time Constant Adjustment Method for the Low Pass
The gain can be set to any convenient value. In this example, G0 = 1 is obtained
by eliminating R4 and using a direct connection for R3 . Then the filter acts as
a “follower” below the break frequency. For a 2 pole Butterworth filter we can
use
C2 = 2C1
(5)
R1 = R2
(6)
1
R1 = √
2 2πfc C1
(7)
and
High Pass Filters
The high pass filter is shown in Fig. 2.
Figure 2: The high pass filter
Gain Adjustment Method for the High Pass
Gain adjustment method. Set R1 = R2 and C1 = C2 . A convenient capacitor
size is selected and the resistor size is calculated to obtain the desired breakfrequency.
3
R1 =
1
2πfn−1 fc C1
(8)
The gain is the same as the low pass case. R3 is given by
R3 = R4 (G0 − 1)
(9)
G0 and fn are taken from the table at the end of the lab. The ffc term in the
Butterworth gain expression is inverted relative to the low pass filter.
G = G0
2n
fc
f
(10)
+1
where n is the total number of poles in the filter.
In this case, the gain drops rapidly when f is less than the break frequency.
Band Pass Filter
The band pass filter is shown in Fig. 3.
Figure 3: The band pass filter
The gain of this circuit is a maximum (Gr ) at the resonant frequency fr .
4
Gr =
fr2 =
1
R2 C2
R1 C1 + C2 1 + GA0
1+
2
R1
R3
1+
(2π) τ1 τ2 1 −
G0
A
C2
C1 A
(11)
(12)
where
τj = Rj Cj
(13)
A is the open loop gain of the op amp at the resonance frequency,
A=
fT
fr
(14)
fT is the gain frequency product of the op amp.
G0 =
R2
= 2πfr C2 R2
χc2
(15)
When the open loop gain is large, the two terms containing A−1 can be neglected.
fr2 =
1+
R1
R3
(2π)2 τ1 τ2
(16)
Therefore, the two time constants set the minimum resonance frequency, but fr
can be increased by making R3 smaller than R1 . The band-pass (B) is defined
as the frequency interval between the high and low break-frequencies (i.e., the
frequencies at which gain is decreased by 30%).
B=
1
2
2πR2 C1 C1C+C
2
(17)
A CA3140 op amp will be used for all circuits. The power supply connections
(±15 V)should be connected to each circuit.
5
1
Low Pass Filters
1. Use the values R1 , C1 , and C2 given in Table 1 to calculate the values of
R1 , R2 , and R3 needed to obtain the specified break frequency fc using
the gain adjustment method.
2. Calculate the gain of the filter at 0.5, 1, 2, 4, and 10 times fc .
3. Build the circuit in Fig. 1. Measure the break frequency and gain at 0.5,
2, 4, and 10 times the measured break frequency. Use a 10 Vpp sine wave
input signal.
4. Use the time constant adjustment method for a two pole, G0 = 1 Butterworth filter. Use the values of C1 given and calculate the values of R1 ,
R2 , and C2 needed to obtain the specified fc and Butterworth frequency
response.
5. Calculate G at 0.5, 1, 2, 4, and 10fc.
6. Set up the circuit using the values calculated in step 4 of this section.
Measure the break frequency and gain at 0.5, 1, 2, 4, and 10 times the
measured break frequency. Use a 10 Vpp sine wave.
7. Use the gain adjustment method for a four pole Chebyshev (0.5 dB) filter.
Use the components given in Table 1. Calculate R1 , R2 , and R3 for both
stages and total gain. You do not need to build this filter.
2
High Pass Filter
1. Use the values of R4 , C1 , and C2 given to calculate the values of R1 , R2 ,
and R3 needed to obtain the specified break frequency.
2. Calculate the gain of the filter at 2, 1, 0.5, 0.25, and 0.1 times fc .
3. Set up the circuit shown in Fig. 2 as designed in the first step of this
section. Measure the break frequency and the gain at 2, 1, 0.5, 0.25, and
0.1 times the measured break frequency. Use a 5 Vpp sine wave for the
input signal.
3
Band Pass Filters
1. Assume the open loop gain is large enough that A−1 terms may be neglected. Calculate the approximate resonant frequency fr .
2. Use the approximate resonant frequency to calculate fr including the A−1
terms.
6
Step
1.1 – 1.3
1.4 – 1.6
1.7
2.1 – 2.3
3.1 – 3.4
3.5 – 3.6
R1
C
C
C
C
1K
1K
R2
C
C
C
C
100K
100K
R3
C
D
C
C
X
200
R4
5.1K
X
5.1K
5.1K
X
X
C1 (nF)
1
1
1
1
5
5
C2 (nF)
1
C
1
1
10
10
fc (kHz)
12
12
12
12
-
fn
1
1
R
1
-
G0
R
1
R
R
-
Table 1: Component values. X = not included, D = direct connection, C =
calculated value, R = read from table. fT = 3.7 MHz for a CA3140
3. Calculate the gain at resonance, Gr , and the bandwidth B.
4. Set up the circuit shown in Fig. 3 using the values given in the Table ??.
Measure fr , Gr , and B. B is the interval between the two frequencies
when G = 0.7Gr . The input signal should be small so that vo is not too
large at resonance. vi = 20 mVpp is appropriate. Be sure to watch the
input voltage as frequency is changed to ensure that vi is constant.
5. The resonance will shift to a higher frequency when R3 is included. Calculate the change in fr .
6. Add R3 given in the table and measure fr and Gr . The decrease in Gr is
produced by inaccurate components and a low quality factor ( GA0 ).
Components Required
1. Op Amps: (1) CA3140
2. Resistors: (1) 200 Ω, (1) 1kΩ, (2) 9.1 kΩ, (1) 3 kΩ, (1) 5.1 kΩ, (2) 13 kΩ,
(1) 100 kΩ
3. Capacitors: (2) 0.1 μF, (2) 1 nF, (2) 2 nF, (1) 5 nF, (1) 10 nF
7