Download PROBABILITY DISTRIBUTIONS A discrete random variable X takes

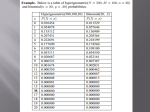
PROBABILITY DISTRIBUTIONS
A discrete random variable X takes value x with probability p(x). The probability
distn specifies p(x) for each possible value x. For example, if I flip a fair coin twice,
the number of heads (X) is a random variable with probability distn
Number of heads
Probability
0
1
2
1/4
1/2
1/4
MEAN AND VARIANCE OF A DISTRIBUTION
The expectation, or mean value of X is
E (X) =
∑ xp(x)
Similarly, E (X2)=∑ x2 p (x) , etc. The variance of X is
var(X) = E(X – m)²,
where m = E(X). An alternative formula for the variance is E(X²) – m².
For the coin example,
E(X) = 0 × (1/4) + 1 × (1/2) + 2 × (1/4) = 1,
var(X) = (-1)² × (1/4) + 0² × (1/2) + 1² × (1/4) = 1/2
The mean of the distn is 1. This is also the mode of the distn (the most probable
value).
The mean is a measure of location or 'central tendency'. Variance measures the
spread (dispersion) of the distn.
The expectation terminology dates from 18th century games of chance. Consider
the following game: you pay me $1 (the stake). A fair coin is then flipped. If it falls
heads, I return the stake and pay an additional $1. If tails, I keep the stake and
pay nothing. Is this a fair game?
Your return is a random variable, determined by the flip of the coin. The expected
return is 2 x 0.5 + 0 x 0.5 = 1. This is exactly equal to the stake: the game is fair.
BINOMIAL DISTRIBUTION
A coin with probability p of landing heads and q of landing tails is flipped three
times.
Sequence
Probability
Heads
Probability
TTT
q³
0
q³
HTT
THT
TTH
pq²
pq²
pq²
1
3pq²
HHT
HTH
THH
p²q
p²q
p²q
2
3p²q
HHH
p³
3
p³
Note that q³ + 3pq² + 3p²q + p³ = (q + p)³ = 1.
Now consider what happens when the coin is flipped n times. The probability of
obtaining any particular sequence of x heads and n – x tails is the product of n
numbers, x of which are equal to p, and n – x of which are equal to q. The number
of such sequences is the number of ways of choosing x positions from n for the
heads. Therefore, probability of x heads is
()
x n−x
p (x) = n p q
(x=0, … , n)
x
For the binomial distn, mean and variance are
E(X) = np, var(X) = npq.
Note also that E(X/n) = p, var(X/n) = pq/n.
Example: Two black-coated animals both carry the recessive allele for red coat
colour. The probability that they produce a red calf is 1/4. This is independently true
for each offspring. Among 4 progeny, the number of red calves has a binomial distn
with n = 4 and p = 1/4.
# red calves
Probability
0
0.3164
1
0.4219
2
0.2109
3
0.0469
4
0.0039
The mean number of red calves is
0 x 0.3164 + 1 x 0.4219 + … = 1, or more simply 4 x 0.25 = 1.
A discrete distribution is usually displayed as a bar chart, with the area of the bar
representing probability. The example below shows the binomial distribution with
n = 16 and p = 1/4. This is a skew distn: the right tail is longer than the left tail.
MULTINOMIAL DISTRIBUTION
The binomial distn arises when there are n trials, and each trial has two possible
outcomes. (A trial is an opportunity for the event to happen.) The multinomial distn
arises when each trial has more than two possible outcomes. For example, a sixsided “die” is thrown sixty times, with the following results:
Score
Frequency
1
8
2
7
3
12
4
10
5
11
6
12
Total
60
Is the die fair? Or is there evidence of bias in favour of certain scores? You will
learn how to answer such questions later in the course.
HYPERGEOMETRIC DISTRIBUTION
A box contains r red balls and b black balls (r + b = N). A random sample of n balls
is removed from the box, without replacement. The probability that there are x red
balls and y black balls in the sample (x + y = n) is
(rx )(by )
(Nn)
The denominator is the number of possible samples. The two numbers in the
numerator are (i) the number of ways the x red balls can be chosen, (ii) the number
of ways that the y black balls can be chosen.
Example: a lottery.
A box holds balls numbered 1 to 59. You choose six of these (red). Think of the
remaining 53 balls as black. A random sample of six balls is removed from the box.
What is the probability that x of the chosen balls are in the sample, for x = 0 to 6?
# balls
Probability
0
0.5095
1
0.3821
2
0.0975
3
0.0104
more than 3
0.0005
The chance of “hitting the jackpot” (all 6 chosen balls in the sample) is about 1 in
45 million.
Sampling with and without replacement
If we sample without replacement, the number of red balls in the sample has a
hypergeometric distn. Sampling with replacement, the distn is binomial with index n
and parameter p = r/N.
For the hypergeometric distn,
E(X) = np,
var(X) = npq(N – n)/(N – 1)
where p = r/N and q = b/N. The mean of the hypergeometric distn is the same as
the mean of the binomial distn we would obtain if sampling with replacement, but
the variance is smaller by a factor (N – n)/(N – 1).
In general, sampling without replacement generates more complicated probability
distns than sampling with replacement, but when the size of the sample (n) is small
relative to the size of the population (N) the two distns are not very different. When
sampling without replacement, we sometimes use the simpler results appropriate to
sampling with replacement as an approximation.
POISSON DISTRIBUTION
The Poisson distn arises as the limit of the binomial distn as n tends to infinity and p
tends to zero while the product np = m remains constant (distn of rare events).
At the limit, the binomial probability becomes
x
m exp(−m)
x!
Possible values are x = 0, 1, 2,
…
(to infinity, theoretically).
This is the Poisson distn with parameter m. The mean and variance of the distn are
both equal to m.
Exponential function
exp(x) is limit as n tends to infinity of the sequence
n
(1 + x/n)
In this form we can see the connection between binomial and Poisson distributions.
The alternative definition as the sum of the infinite series
2
3
1 + x + x + x + ⋯
2!
3!
shows that Poisson probabilities sum to 1.
Example: birthdays
Each member of a group of 365 people is asked whether today is his or her
birthday. Let Y equal the number of people who say “yes”. The probability that Y
equals zero is (1 – 1/365) raised to the power 365, approximately exp( – 1) = 0.368.
More generally we can show that (approximately)
−1
Pr (Y = y) = e / y!
(Y has a Poisson distn with mean 1.)
# birthdays
Probability
0
0.368
1
0.368
2
0.184
3
0.061
4 (or more)
0.019
THE POISSON PROCESS
Events occur singly, at random, at times or locations T1,T2, … , such that the
numbers of events in non-overlapping intervals are independent random variables.
Probability that n events occur in the time interval (0,t) is
n
(λ t) exp(−λ t)/n!
The number of events has a Poisson distn with mean m =λt. The “rate” parameter λ
measures the average rate at which events occur.
Example: vehicle arrivals
Assume that vehicles arrive at a census point in a Poisson process. If, on average,
one vehicle passes the fixed point every 20 seconds, what is the probability that
there will be at most 2 arrivals in a two-minute period?
Average arrival rate (λ) is 3 per minute. Number of events X in a period of length
2 minutes has a Poisson distn with mean 6. Then
Pr (X < 3) = exp (−6) [1+ 6 + 18]= 0.062
(Or use Cambridge Tables, No. 2).
Poisson distribution: examples
As the distn of rare events:
1. Number in a large group with birthday on a particular day;
2. Number of misprints per page of a book;
3. Annual number of deaths from horse-kicks in the Prussian cavalry
Arising from the Poisson process:
1. Radioactive disintegrations over time;
2. Number of bacteria per unit area of a petri dish;
3. Recombination events in a length of chromosome;
4. Vehicles passing a fixed point.
CONTINUOUS DISTRIBUTIONS
The r.v.s we have looked at so far have taken integer values 0,1,2, etc. They have
arisen as a result of counting: how many times did a particular event occur? We call
such r.v.s “discrete”. A “continuous” r.v. has values that are not restricted to a
discrete set: if x1 and x2 are two possible values of the r.v., any value between x1
and x2 is also possible.
EXPONENTIAL DISTRIBUTION
A simple example of a continuous r.v. is the time T to the first event in a Poisson
process of rate λ. Let Nt denote the number of events between time 0 and time t.
This has a Poisson distn with mean λt, so
Pr (T > t )= Pr (Nt = 0)=exp (−λ t) .
The distn of T is called the exponential distn. It can be used to describe the lengths
of chromosome segments between recombination events, the times between random
events (e.g. vehicles passing a road census point), or the lifetimes of components
subject to failure at a constant rate. The mean of the distn is 1/λ.
The cumulative distribution function of a continuous r.v. X is defined in exactly the
same way as for a discrete r.v., but the discrete probability function is replaced by
a probability density function f(x), such that the probability that X lies in a short
interval (x, x + h) is approximately hf(x) for small h.
The probability that a<X<b is given by the integral
b
Pr (a < X < b)=∫ f (x) dx
a
With a continuous distn, we can only attach a probability to an interval of values,
not to a single value.
The two functions F(x) (cumulative probability function) and f(x) (probability density
function) are related: F(x) is the area under the curve represented by the function f
to the left of x. Thus the probability that a < X < b, F(b) – F(a), is the area under the
probability density function to the left of b and to the right of a.
When looking at a probability density function, it is the area under the curve that is
important, not the value of the function.
THE NORMAL DISTRIBUTION
The normal, or Gaussian, density function is
( )
1 exp − x
2
√2 π
2
Plotting this curve shows a characteristic bell shape, symmetric about zero. A
random variable with this density function is said to be normally distributed, or
Gaussian.
The mean of the distn is 0 and the variance is 1. This is the “standard” form of the
normal distn.
The notation N(m,σ²) denotes a normal distn with mean m and variance σ². If the
distn of X is N(m,σ²), the standardized value (X – m)/σ has a standard normal
distn.
KURTOSIS
Kurtosis measures the thickness of the tails of a distribution. The standard for
comparison is the normal distribution: positive kurtosis indicates a distribution with
thicker tails than the normal distribution.
CENTRAL LIMIT THEOREM
The distn of the average of a sample of size n from almost any distn tends to a
normal distn as n tends to infinity. This result can explain why a trait is normally
distributed (it may be determined by many genes, each of which individually has a
small effect). For example, the distn of heights or weights in a population often
follow a normal distn (at least approximately).
Example: let X be binomial (n, p). The mean and variance of X are np and npq,
where q = 1 – p. For large n, the probability that X lies between r and s (inclusive) is
approximated by the probability that a standard normal r.v. lies between limits
(r − np−0.5)/ √ npq and (s−np + 0.5)/ √ npq
Example: if X is binomial with n=16, p = 1/2, what is Pr (6≤ X ≤10) ?
This is approximated by the probability (0.79) that a standard normal lies between
the limits ±1.25. Exact answer (0.79 to two decimal places) is the sum of five
binomial probabilities.
CUMULATIVE PROBABILITIES AND QUANTILES
We discuss this first for continuous distns (e.g., exponential, normal). The
cumulative distn function for random variable X is F (x )= Pr (X ≤x ) . This is an
increasing function of x with a value between 0 and 1. The corresponding quantile
function Q(p) is the value of x such that F(x) = p, so that Q(p) = x and F(x) = p are
equivalent statements.
The first, second and third quartiles of the distn are Q(0.25), Q(0.5), and Q(0.75).
The second quartile Q(0.5) is also known as the median. Total probability is split by
the median into two equal parts. The three quartiles split the probability into 4 equal
parts. Similarly, four quintiles split into 5 equal parts, nine deciles into 10 equal
parts, 99 percentiles into 100 equal parts. The generic term for medians, quartiles,
etc is 'quantile'. Note that there may be several names for the same quantile. For
example, Q(0.75) could be referred to as third quartile, upper quartile, 75th
percentile, or the 75% point of the distribution. Or it could be called the upper 25%
point, 'upper' indicating that the measured probability is in the upper rather than
the lower tail of the distn.
For some distns, the calculation of F(x) or Q(p) is straightforward. For the unit
exponential distn, F(x) = 1 – exp( --x) and Q(p) = – loge(1 -- p). For most other
distns, the calculation of F(x) requires laborious summation or numerical
integration. E.g., for the standard normal,
x
F (x)= ∫
−∞
1 exp (− u 2 ) du
2
√2 π
Hence the need for statistical tables.
TABLES OF THE NORMAL DISTRIBUTION
Probabilities for the normal and other continuous distns are calculated as areas
under the density function. Statistical tables give cumulative probabilities for the
standard normal distn with zero mean and unit variance.
If necessary, standardize X before referring to tables. For example, if X is N(m,σ²),
what is Pr(m – σ < X < m + σ)?
This is the same as the probability that –1 < (X – m)/σ < +1, the probability that a
standard normal r.v. deviates from its mean value by less than one standard
deviation. Tables of the normal distn give F(1) = 0.8413, so required probability is
F(1) – F(–1) = 0.8413 – (1 – 0.8413) = 0.6826 (draw a picture).
QUANTILES OF THE NORMAL DISTRIBUTION
Here are some frequently used percentiles of the standard normal distn:
Percent
Percentile
90
1.2816
95
1.6449
97.5
1.9600
99
2.3263
If X is N(m,σ²), the quantile is m + xσ, where x is the corresponding quantile of the
standard normal. For example, a r.v. X is normally distributed with mean 100 and
standard deviation 10. What is the upper 2.5% point of its distn? The upper 2.5%
point of the standard normal distn is 1.96 (the probability that a standard normal
exceeds 1.96 is 0.025). The upper 2.5% point of the distn of X is
100 + 10×1.96 = 119.6
TABLES FOR DISCRETE DISTRIBUTIONS
Tables are also required for discrete distns (binomial, hypergeometric, Poisson, etc),
because F(x) may be the sum of a very large number of probabilities. We have to be
slightly more careful when dealing with a discrete r.v. For a purely continuous r.v.,
Pr (X ≤x) and Pr(X < x) are equal, but this is not necessarily the case for a
discrete r.v. For example, suppose X is discrete, taking values 0, 1, 2, etc. If x is
one of the possible values of X, the two probabilities differ by Pr(X = x).
The definition of the median (and other quantiles) is trickier for a discrete distn.
E.g., suppose X takes values 1...4 with equal probability. The cumulative probability
function is a step function with value 1/4 between 1 and 2, 1/2 between 2 and 3,
3/4 between 3 and 4. The median could be defined to be any value between 2 and 3
(e.g. 2.5).
R FUNCTIONS pnorm( ) and qnorm( )
In R, pnorm(x) calculates F(x) and qnorm(p) calculates Q(p) for the standard normal
distn. dnorm(x) gives the probability density function (useful for plotting the normal
curve, but not usually required for probability calculations). There are similar
functions for other distns (dbinom, pbinom, etc).
Examples
1. Number of red calves among four progeny? dbinom(0:4, 4, 1/4)
2. How many birthdays in a group of 365? dpois(0:3, lambda = 1)
3. Vehicle arrivals? ppois(2, lambda = 6)
4. Probability that standard normal deviates from its mean by less than 1 s.d.?
pnorm(1) – pnorm(-1), or 2*pnorm(1) – 1
5. Upper 2.5% point of the standard normal?
qnorm(0.975) or qnorm(0.025, lower.tail = FALSE)
BIVARIATE DISTRIBUTIONS
If two random variables Y1 and Y2 are independently distributed, the conditional
distn of Y1 does not depend on the value of Y2. An example of two variables which
are not independently distributed are height and weight: the distn of weights among
a sub-population of short people differs from the distn among a sub-population of
tall people. There is a positive covariance (or correlation) between height and
weight.
COVARIANCE
The covariance between r.v.s Y1 and Y2 is
cov(Y1,Y2) = E[(Y1 – m1)(Y2 – m2 )] = E(Y1Y2) – m1m2
The correlation between Y1 and Y2 is a scaled version of the covariance which
removes dependence on units of measurement:
cor(Y1,Y2) = cov(Y1,Y2)/σ1σ2
where σ1 and σ2 are the standard deviations of Y1 and Y2.
Covariance between r.v.s has an effect on the variance of the sum:
var(Y1 + Y2) = var(Y1) + var(Y2) + 2 cov(Y1,Y2).
More generally, the variance of a sum of r.v.s is the sum of their variances plus
twice the sum of the pairwise covariances.
The variance of the sum of independent r.v.s is the sum of their variances.
There are bivariate versions of many distns, but the bivariate normal distn is the
only example we deal with on this course.
PROBABILITY (DENSITY) FUNCTION
If Y1 and Y2 are discrete r.v.s, the probability function of their joint distn is
f(y1, y2) = Pr(Y1 = y1, Y2 = y2)
for all possible pairs of values (y1, y2). If the distn is continuous, the probability
density function f(y1, y2) is such that the probability that the random point (Y1,Y2)
falls in a small rectangle with corners at (y1, y2) and (y1 + h, y2 + k) is approximately
hk f(y1, y2).
BIVARIATE NORMAL DISTRIBUTION
The probability density function f(y1, y2) of the standard bivariate normal distn is
proportional to
exp
[
2
2
−(y 1 + y2 −2 ρ y1 y 2 )
2
]
The standard distn has zero means and unit variances. The general form of the
distn allows arbitrary mean values and variances. The random vector (Y1,Y2) then
has mean vector (m1, m2) and covariance matrix
(
2
σ1
ρ σ1 σ2
2
ρ σ1 σ 2
σ2
)
The figure below shows the p.d.f. of a bivariate normal distn with equal variances
and a correlation of ρ = 0.5 between the two variables.
MARGINAL AND CONDITIONAL DISTRIBUTIONS
Generating a pair of values from a bivariate distn can be done in two stages.
1. Select Y1 from its marginal distn.
2. Select Y2 from the conditional distn of Y2, given Y1.
For the standard bivariate normal distn,
Marginal distn of Y1 is N(0,1),
Conditional distn of Y2, given Y1, is normal with mean and variance
E(Y2|Y1) = ρY1, var(Y2|Y1) = (1 – ρ2)
The figure below shows the same example of a bivariate normal distn using
probability contours. Also shown are the two regression (or prediction) lines,
representing E(Y2| Y1) and E(Y1| Y2). At zero correlation, these line are at right
angles, and with perfect correlation, the two lines merge into one.
MULTIVARIATE NORMAL DISTRIBUTION
The bivariate normal distn generalizes to the multivariate normal distn for three or
more variables. Covariances between pairs of variables are shown as a covariance
matrix with variances on the diagonal and covariances off-diagonal.
SUMS OF SQUARES, DEGREES OF FREEDOM
The sum of squared deviations ∑ (Yi − Ȳ)2 is sometimes called the corrected sum of
squares and written as Syy. For sample size n = 2, it can be written in two different
ways as
2
(Y 1 − Ȳ)
2
+ (Y 2 − Ȳ)
2
= (1 /2) (Y 1 − Y 2 )
In this case (when n = 2), Syy appears to be the sum of two squares, but can be
reduced to a single square by algebraic manipulation. When n = 2, we say Syy has 1
'degree of freedom'. In the same way, the corrected sum of squares for a sample of
size n can be written as the sum of n – 1 squares, and has n – 1 degrees of
freedom.
It can be shown that Syy has expectation (n – 1)σ². An unbiased estimate of σ² is
obtained by dividing Syy by ( n – 1). This is why the formula for the sample variance
has n – 1 on the denominator rather than n.
SAMPLING DISTRIBUTIONS
The chi-squared, t, and F dists arise when sampling from the normal distn.
Assume that Y 1 … Y n is a random sample from N(m,σ²). Define sample mean Ȳ
and sample variance S² as
−1
Ȳ =n
n
∑ Yi
i=1
2
−1
, S =(n −1)
n
∑ (Yi − Ȳ)2
i=1
a) The distn of the sample mean Ȳ is N(m,σ²/n), and the standardized value of the
sample mean
√ n ( Ȳ −m )/σ
has a standard normal distn.
b) The distribution of (n – 1)S²/σ² is chi-squared with n – 1 degrees of freedom.
This is the distn of the sum of squares of n – 1 independent standard normal
variables.
c) The distn of √ n ( Ȳ −m)/S is called Student's t distn with n – 1 degrees of
freedom. The shape of this distn depends on n – 1, the number of degrees of
freedom associated with S². When this number is large, the t distn is close to
standard normal. When the number is small, the t distn has thicker tails (shows
positive kurtosis). The quantiles of the t distribution are always further from zero
than the corresponding quantiles of the standard normal distribution.
d) When S21 and S22 are independent estimates of σ², with degrees of freedom n1
and n2, the distn of S21 /S22 is called the F distn with n1 and n2 degrees of freedom.
For example, the sample variance S² is an estimate of σ², with n – 1 degrees of
freedom, and so also is n (Ȳ − m)2 , with 1 degree of freedom. The ratio
n (Ȳ − m)2 /S2 has an F distn with 1 and n – 1 d.f.
There are various relationships among the three distns. For example, when T has a
t distn with ν d.f., T2 has an F distn with 1 and ν d.f.
R functions pchisq( ), pt( ), pf( ), etc are available for calculating cumulative
probabilities and qchisq( ), etc, for quantiles. Often these are not needed because
the calculation is done internally by a function such as lm( ) or t.test( ).
GENERALISATION
The corrected sums of squares can be regarded as a 'residual' sum of squares,
after adjusting each observation by subtracting the sample mean. In simple linear
regression, a residual sum of squares for Y is corrected for the mean and also for
regression on an explanatory variable X. In this case, the number of degrees of
freedom associated with the residual sum of squares is n – 2, where n is sample
size and 2 is the number of terms fitted (intercept, and X). In multiple regression
and anova, the residual sum of squares has n – k degrees of freedom, where k is
the total number of terms fitted. (For example, in one-way anova, k is the number of
groups.) In general, the residual variance has expectation (n – k)σ², and an
unbiased estimate of σ² is obtained by dividing the residual variance by (n – k). In
the context of multiple regression or anova, this estimate is called the residual mean
square.