Download Section 4.4 and 4.5

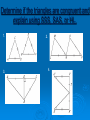
Warm Up
1.) Find the measure of the exterior angle.
2x0
(5x – 2)0
760
2.) Find the values of x and y given
B E
420
A
(5x + 2)0
D
870
3y0
C
F
Geometry
Sections 4.4 & 4.5
Prove Triangles Congruent Using SSS, SAS, HL
Objective:
SWBAT use sides and angles of triangles to prove
congruence.
Side Names of Triangles
Right Triangles: side across from right angle is the hypotenuse,
the remaining two are legs.
leg
hypotenuse
leg
All other triangles: All sides are called legs.
leg
leg
leg
Proving Triangles Congruent Using
SSS, SAS, HL
Two triangles are congruent when all three angles are
marked congruent and all three sides are marked
congruent.
There are other ways to prove two triangles are
congruent. We will discuss three ways today.
Once two triangles have been proven congruent to each
other, then you know all the corresponding sides and
angles are also congruent.
Postulate 19
Side-Side-Side (SSS) Congruence
Postulate:
If three sides of one triangle are congruent to three sides
of a second triangle, then the two triangles are
congruent.
Example:
because of SSS.
A
D
B
C E
F
Postulate 20
Side-Angle-Side (SAS) Congruence
Postulate:
If two sides and the included angle of one triangle are
congruent to two sides and the included angle of a
second triangle, then the two triangles are congruent.
** included angle is the angle in-between the two sides**
 Example:
because of SAS.
P
Q
L
R
M
N
Theorem 4.5
Hypotenuse- Leg (HL) Congruence
Theorem:
If the hypotenuse and a leg of a right triangle are
congruent to the hypotenuse and leg of a second
right triangle, then the two triangles are
congruent.
Example:
because of HL.
A
B
X
C
Y
Z
Does not make
triangles congruent.
ASS does not make triangles congruent.
Determine if the triangles are congruent and
explain using SSS, SAS, or HL.
1.
3.
2.
4.
Determine if the triangles are congruent and
explain using SSS, SAS, or HL.
5.
6.
7.
8.
Write a Proof

Homework
Page 234-235 # 5, 7, 18, 24, 26
Page 241 -242
# 10, 12, 20, 22