Download Honors Geometry Section 10.3 Trigonometry on the Unit Circle

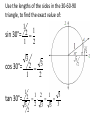
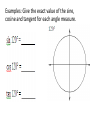
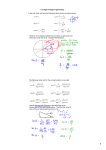
Honors Geometry Section 10.3
Trigonometry on the Unit Circle
Trigonometry has been used by many cultures
for over 4,000 years! On page 870 of your text is
a table of approximate values for the sine,
cosine and tangent of angles between 0° and
90°. These are the same approximate values
your calculator will give you. You may wonder
where these values come from? One
way of finding some of these values is to use the
unit circle, a circle with its center
_______________
at the origin (0, 0) of the coordinate plane and
1
with a radius of ___.
Let’s put a 30° angle in the coordinate
plane so that its vertex is at the origin, one
side lies on the positive x-axis and the
second side lies in quadrant I. Call the
point where the second side intersects the
unit circle point A.
Draw a line from point A perpendicular to the xaxis. A 30-60-90 triangle is formed. Which side
of this triangle do we know the length of?
1
___________
hypotenuse What is its length? ____
What are the lengths of the two legs in this 3060-90 triangle?
Use the lengths of the sides in the 30-60-90
triangle, to find the exact value of:
1
1
2
sin 30°=

1
2
3
3
2
cos 30°=

1
2
tan 30°=
1
2  1 2  1  3
2 3
3
3
3
2
Let’s do the same with a 45° angle.
Use the lengths of the sides in the 45-45-90
triangle, to find the exact value of
2
sin 45°=
2  2
1
2
2
cos 45°=
2  2
1
2
2
tan 45°=
2
a 2 1
2 1
2
a
1
2
2


2
2
2
We can extend the unit circle to include angles
greater that 90° and negative angles by
discussing the angle of rotation.
An angle of rotation has its vertex at the origin
and one side on the positive x-axis. The side on
the x-axis is called the _____
initial side of the angle.
The second side of the angle, called the
_______side, is obtained by doing a rotation
terminal
positive
either counterclockwise for ________angles
or
negative angles.
clockwise for ________
Unit Circle Definition of Sine and Cosine: Let  (the
Greek letter theta) be an angle of rotation. Sin  is
y-coordinate
equal to the ____________of
the point where the
terminal side intersects the unit circle and cos  is
x-coordinate of this point.
equal to the ____________
sin 
Tan  equals
cos 
cos sin 
sin 
cos 
Examples: Give the exact value of the sine,
cosine and tangent for each angle measure.
Examples: Give the exact value of the sine,
cosine and tangent for each angle measure.