* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Ch25 - MrsCDsAPPhysics
Lumped element model wikipedia , lookup
Galvanometer wikipedia , lookup
Power MOSFET wikipedia , lookup
Nanofluidic circuitry wikipedia , lookup
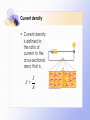
Resistive opto-isolator wikipedia , lookup
Negative resistance wikipedia , lookup
Giant magnetoresistance wikipedia , lookup
Superconductivity wikipedia , lookup
Rectiverter wikipedia , lookup
Ch. 25 Current, Resistance, and EMF AP Physics C 1 Electric Current • There needs to be an E-field present. 2 Motion of ball analogous to an electron moving in a metallic conductor with the presence of an electric field. 3 Conventional current • Direction of the net flow of positive charges • The rate that the charge is moving is given by: dq I dt 4 Concentration of charges • Suppose there are n charged particles per unit volume. This is called the concentration of charges. 5 Drift velocity • If all the particles are moving with the same drift velocity, vd, how many particles flow at the end of the conductor in a time interval of dt? 6 Current density • Current density is defined to the ratio of current to the cross-sectional area; that is, I J A 7 Sample Problem #1 • An 18-gauge copper wire (the size usually used for lamp cords) has a nominal diameter of 1.02 mm. This wire carries a constant current of 1.67 A to a 200-watt lamp. The density of free electrons is 8.5 x 1028 electrons per cubic meter. Find the magnitudes of • The current density and • The drift velocity. 8 Sample Problem #2 • Suppose that we replaced the wire in the previous sample problem with a 12-gauge copper wire, which has twice the diameter of the 18-gauge wire. If the current remains the same, what is the new magnitude of the drift velocity? 9 Sample Problem #3 • The 12-gauge copper wire in a typical residential building has a cross-sectional area of 3.31 x 10-6 m2. If it carries a current of 10.0 A, what is the drift speed of the electrons? Assume that each copper atom contributes one free electron to the current. The density of copper is 8.95 g/cm3 and its molar mass is 63.54 g/mol. 10 Sample Problem #4 • If a copper wire carries a current of 80.0 mA, how many electrons flow past a cross-section of the wire in 10.0 min? 11 Non-Electrostatic Electric Field • An electric field exists in the conductor because the charges are in motion due to the difference in potential. In some materials, the current density is proportional to the electric field. 12 Ohm’s Law • σ is the conductivity of the conductor, J E • The reciprocal of the conductivity is known as the resistivity of the conductor, ρ. • Pg. 948, Table 25.1. 13 Ohmic Materials • Materials that obey Ohm’s law V EL J J R V V E L I V A L L V A I IR 14 Different Materials • Ohmic • Vacuum-tube diode • Semiconductor diode 15 Resistance • R = resistance • 1 volt/ampere=1 ohm (Ω) • Factors affecting resistance • Temperature • R(T) = Ro [1 + a (T - To)] • Type of material • Length of material • Cross-sectional area of material 16 Sample Problem #5 • Calculate the resistance of an aluminum cylinder that is 10.0 cm long and has a cross-sectional area of 2.00 x 10-4 m2. The resistivity for aluminum is 2.75 x 10-8 Ω-m. 17 Sample Problem #6 • Calculate the resistance per unit length of a 22-gauge Nichrome wire, which has a radius of 0.321 mm. The resistivity of Nichrome is 100 x 10-8 Ω-m. • If a potential difference of 10 V is maintained across a 1.0 m length of the Nichrome wire, what is the current in the wire? • What is the resistance of a 6.0 m length of 22-gauge Nichrome wire? • How much current does the wire carry when connected to a 120 V source of potential? • Calculate the current density and electric field in the 22gauge Nichrome wire when it carries a current of 2.2 A. 18 Sample Problem #7 • Coaxial cables are used extensively for cable television and other electronic applications. A coaxial cable consists of two cylindrical conductors. The gap between the conductors is completely filled with silicon and current leakage through the silicon is unwanted. The cable is designed to conduct current along its length. The radius of the inner conductor is 0.500 cm, the radius of the outer one is 1.75 cm, and the length of the cable is 15.0 cm. Calculate the resistance of the silicon between the conductors. The resistivity of silicon is 2300 Ω-m. 19 Sample Problem #8 • A resistance thermometer, which measures temperature by measuring the change in resistance of a conductor, is made from platinum and has a resistance of 50.0 Ω at 20.0o C. When immersed in a vessel containing melting indium, its resistance increases to 76.8 Ω. Calculate the melting point of the indium. The temperature coefficient of resistivity for platinum is 3.92 x 10-3 (oC)-1. 20 Sample Problem #9 • An 18-gauge copper wire has a diameter of 1.02 mm and it carries a current of 1.67 A. Find: • The cross-sectional area of the wire • The electric field magnitude in the wire • The potential difference between two points in the wire 50.0 m apart • The resistance of a 50.0 m length of the wire • Suppose that the temperature is at 20o C, what is its resistance at 100o C? 21 Internal Resistance and EMF • Sources of emf, ε • Batteries • Generators • Internal resistance, r • Resistance that the charge encounters as it moves through the source 22 Voltage rises and drops in a circuit: • Ideal source •r=0 Vab IR • Real source Vab Ir IR 23 Sample Problem #10 • Draw a schematic diagram showing a source (a battery) with an emf of 12 V and an internal resistance of 2 Ω. Also, show a voltmeter connected across the battery and ammeter connected to the battery. There is no external resistance connected. This is an example of an open circuit. What are the readings of the idealized voltmeter and idealized ammeter? 24 Sample Problem #11 • A 4 Ω resistor is connected to the battery in the circuit described in sample problem #10. What are the readings of the voltmeter and ammeter now? 25 Sample Problem #12 • The external resistance in sample problem #11 is replaced with a zero resistance. This is called a short circuit. What are the meter readings now? 26 Sample Problem #13 • A battery has an emf of 1.5 V and an internal resistance of 0.10 Ω. When the battery is connected to a resistor, the terminal voltage is 1.3 V. What is the resistance of the resistor? 27 Power • V = U / Q = dU / dQ • I = dQ / dt • V = dU / dQ = dW / dQ • dW = V dQ = V I dt • P = dW / dt = V I • the rate of delivering energy to a circuit element having a potential difference across it of V 28 Power Output • P = dW / dt = V I • P = VI = (ε – Ir)I = (IR)I • P = VI = I I 2 r I 2 R • Rate of conversion of chemical energy to electric energy, I • Rate of electrical energy dissipated by the internal resistance, I 2r • Rate of electrical energy dissipated by the external resistance, I 2 R 29 Sample Problem #14 • A battery has an emf of 12.0 V and internal resistance of 0.05 Ω. Its terminals are connected to a load resistance of 3.00 Ω. • Find the current in the circuit and the terminal voltage of the battery. • Calculate the power delivered to the load resistor, the power delivered to the internal resistance of the battery, and the power delivered by the battery. 30 Sample Problem #15 • Show that the maximum power delivered to the load resistance R in a circuit occurs when the load resistance matches the internal resistance; that is, when R = r. 31 Power Input • How is this equation different when you are charging a battery? • P = VI = I I 2 r I 2 R 32