Download math 214 (notes) - Department of Mathematics and Statistics

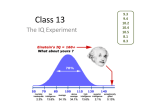
MATH 214 (NOTES)
Math 214
Al Nosedal
Department of Mathematics
Indiana University of Pennsylvania
MATH 214 (NOTES) – p. 1/6
"Pepsi" problem
A market research consultant hired by the Pepsi-Cola Co. is
interested in determining the proportion of IUP students who
favor Pepsi-Cola over Coke Classic. A random sample of
100 students shows that 40 students favor Pepsi over Coke.
Use this information to construct a 95% confidence interval
for the proportion of all students in this market who prefer
Pepsi.
MATH 214 (NOTES) – p. 2/6
Bernoulli Distribution
xi =
(
1 i-th person prefers Pepsi
0 i-th person prefers Coke
µ = E(xi ) = p
σ 2 = V (xi ) = p(1 − p)
Pn
xi
Let p̂ be our estimate of p. Note that p̂ = n = x̄. If n is
"large", by the Central Limit Theorem, we know that:
x̄ is roughly N (µ, √σn ), that is,
i=1
q
p̂ is roughly N p, p(1−p)
n
MATH 214 (NOTES) – p. 3/6
Interval Estimate of p
Draw a simple random sample of size n from a population
with unknown proportion p of successes. An (approximate)
confidence interval for p is:
p̂ ± z∗
r
p̂(1 − p̂)
n
!
where z∗ is a number coming from the Standard Normal that
depends on the confidence level required.
Use this interval only when:
1) n is "large" and
2) np̂ ≥ 5 and n(1 − p̂) > 5.
MATH 214 (NOTES) – p. 4/6
Problem 31 (page 322)
A simple random sample of 400 individuals provides 100
Yes responses.
a. What is the point estimate of the proportion of the
population that would provide Yes responses?
b. What is the point estimate of the standard error of the
proportion, σp̂ ?
c. Compute the 95% confidence interval for the population
proportion.
MATH 214 (NOTES) – p. 5/6
Solution
a. p̂ =
100
400
= 0.25
b. Standard error of p̂ =
c. p̂ ± z∗
q
(p̂)(1−p̂)
n
0.25 ± 1.96(0.0216)
(0.2076, 0.2923)
q
(p̂)(1−p̂)
n
=
q
(0.25)(0.75)
400
= 0.0216
MATH 214 (NOTES) – p. 6/6
Problem 32 (page 323)
A simple random sample of 800 elements generates a
sample proportion p̂ = 0.70.
a. Provide a 90% confidence interval for the population
proportion.
b. Provide a 95% confidence interval for the population
proportion.
MATH 214 (NOTES) – p. 7/6
Solution
a. p̂ ± z∗
q
0.70 ± 1.65
(p̂)(1−p̂)
n
q
(0.70)(1−0.70)
800
0.70 ± 1.65(0.0162)
(0.6732, 0.7267)
b. 0.70 ± 1.96(0.0162)
(0.6682, 0.7317)
MATH 214 (NOTES) – p. 8/6
Problem 35 (page 323)
A survey of 611 office workers investigated telephone
answering practices, including how often each office worker
was able to answer incoming telephone calls and how often
incoming telephone calls went directly to voice mail. A total
of 281 office workers indicated that they never need voice
mail and are able to take every telephone call.
a. What is the point estimate of the proportion of the
population of office workers who are able to take every
telephone call?
b. At 90% confidence, what is the margin of error?
c. What is the 90% confidence interval for the proportion of
the population of office workers who are able to
take every telephone call?
MATH 214 (NOTES) – p. 9/6
Solution
a. p̂ = 281
611 = 0.46
b.q
Margin of errorq=
z∗
(p̂)(1−p̂)
n
c. p̂ ± z∗
= 1.65 (0.46)(0.54)
= 1.65(0.0201) = 0.0332
611
q
(p̂)(1−p̂)
n
0.46 ± .0332
(0.4268, 0.4932)
MATH 214 (NOTES) – p. 10/6
Problem 33 (page 323)
In a survey, the planning value for the population proportion
is p∗ = 0.35. How large a sample should be taken to provide
a 95% confidence interval with a margin of error of 0.05?
Solution.
n=
z∗ 2 ∗
∗)
p
(1
−
p
E
=
(Always round up).
1.96 2
(0.35)(1 − 0.35)
0.05
= 350
MATH 214 (NOTES) – p. 11/6
Determining the Sample Size
Sample Size for an Interval Estimate of a Population
Proportion.
n=
z 2
∗
E
p∗ (1 − p∗ )
In practice, the planning value p∗ can be chosen by one of
the following procedures.
1. Use the sample proportion from a previous sample of the
same or similar units.
2. Use a planning value of p∗ = 0.5.
MATH 214 (NOTES) – p. 12/6
Problem 34 (page 323)
At 95% confidence, how large a sample should be taken to
obtain a margin of error of 0.03 for the estimation of a
population proportion? Assume that past data are not
available for developing a planning value for p∗ .
Solution.
n=
z∗ 2 ∗
∗)
p
(1
−
p
E
=
(Always round up).
1.96 2
(0.5)(1 − 0.5)
0.03
= 1068
MATH 214 (NOTES) – p. 13/6
Problem 39 (page 323)
The percentage of people not covered by health care
insurance in 2003 was 15.6%. A congressional committee
has been charged with conducting a sample survey to
obtain more current information.
a. What sample size would you recommend if the
committee’s goal is to estimate the current proportion of
individuals without health care insurance with a margin of
error of 0.03? Use a 95% confidence level.
b. Repeat part a) using a 99% confidence level.
MATH 214 (NOTES) – p. 14/6
Solution
a. n =
z∗ 2 ∗
∗)
p
(1
−
p
E
b. n =
z∗ 2 ∗
∗)
p
(1
−
p
E
=
1.96 2
(0.156)(1 − 0.156)
0.03
= 563
=
2.58 2
(0.156)(1 − 0.156)
0.03
= 974
MATH 214 (NOTES) – p. 15/6
CHAPTER 9
HYPOTHESIS TESTS
MATH 214 (NOTES) – p. 16/6
Do you want to become a millionaire?
Let’s say that one of you is invited to this popular show. As
you probably know, you have to answer a series of multiple
choice questions and there are four possible answers to
each question. Perhaps you also have seen that if you don’t
know the answer to a question you could either "jump the
question" or you could "ask the audience".
Suppose that you run into a question for which you don’t
know the answer with certainty and you decide to "ask the
audience". Let’s say that you initially believe that the right
answer is A. Then you ask the audience and only 2% of the
audience shares your opinion. What would you do? Change
your initial belief or reject it?
MATH 214 (NOTES) – p. 17/6
Sweetening colas
Diet colas use artificial sweeteners to avoid sugar. These
sweeteners gradually lose their sweetness over time.
Manufacturers therefore test new colas for loss of sweetness
before marketing them. Trained tasters sip the cola along
with drinks of standard sweetness and score the cola on a
"sweetness score " of 1 to 10. The cola is then stored for a
month at high temperature to imitate the effect of four
months’ storage at room temperature. Each taster scores
the cola again after storage. This is a matched pairs
experiment. Our data are the differences (score before
storage minus score after storage) in the tasters’ scores.
The bigger these differences, the bigger
the loss of sweetness.
MATH 214 (NOTES) – p. 18/6
Sweetening colas (cont.)
Suppose we know that for any cola, the sweetness loss
scores vary from taster to taster according to a Normal
distribution with standard deviation σ = 1. The mean µ for all
tasters measures loss of sweetness, and is different for
different colas.
The following are the sweetness losses for a new cola, as
measured by 10 trained tasters: 2.0 0.4 0.7 2.0 -0.4 2.2 -1.3
1.2 1.1 2.3.
Are these data good evidence that the cola lost sweetness
in storage?
MATH 214 (NOTES) – p. 19/6
Solution
µ= mean sweetness loss for the population of all tasters.
1. State hypotheses. H0 : µ = 0 vs Ha : µ > 0
x̄−µ
√
√ 0 = 1.02−0
2. Test statistic. z∗ = σ/
= 3.23
n
1/ 10
3. P-value. P (Z > z∗ ) = P (Z > 3.23) = 0.0006
4. Conclusion. We would very rarely observe a sample
sweetness loss as large as 1.02 if H0 were true. The small
P-value provides strong evidence against H0 and in favor of
the alternative Ha : µ > 0, i.e., it gives good evidence that the
mean sweetness loss is not 0, but positive.
MATH 214 (NOTES) – p. 20/6
Executives’ blood pressures
The National Center for Health Statistics reports that the
systolic blood pressure for males 35 to 44 years of age has
mean 128 and standard deviation 15. The medical director
of a large company looks at the medical records of 72
executives in this age group and finds that the mean systolic
blood pressure in this sample is x̄ = 126.07. Is this evidence
that the company’s executives have a different mean blood
pressure from the general population?
Suppose we know that executives’ blood pressures follow a
Normal distribution with standard deviation σ = 15.
MATH 214 (NOTES) – p. 21/6
Solution
µ= mean of the executive population.
1. State hypotheses. H0 : µ = 128 vs Ha : µ 6= 128
x̄−µ
√
√ 0 = 126.07−128
2. Test statistic. z∗ = σ/
= −1.09
n
15/ 72
3. P-value. 2P (Z > |z∗ |) = 2P (Z > | − 1.09|) = 2P (Z > 1.09) =
2(1 − 0.8621) = 0.2758
4. Conclusion. More than 27% of the time, a simple random
sample of size 72 from the general male population would
have a mean blood pressure at least as far from 128 as that
of the executive sample. The observed x̄ = 126.07 is
therefore not good evidence that executives differ from other
men.
MATH 214 (NOTES) – p. 22/6
Tests for a population mean
There are four steps in carrying out a significance test:
1. State the hypotheses.
2. Calculate the test statistic.
3. Find the P-value.
4. State your conclusion in the context of your specific
setting.
Once you have stated your hypotheses and identified the
proper test, you or your calculator can do Steps 2 and 3 by
following a recipe. Here is the recipe for the test we have
used in our examples.
MATH 214 (NOTES) – p. 23/6
Z test for a population mean µ
Draw a simple random sample of size n from a Normal
population that has unknown mean µ and known standard
deviation σ . To test the null hypothesis that µ has a specified
value, H0 : µ = µ0
calculate the one-sample z statistic
z∗ =
x̄ − µ0
√σ
n
In terms of a variable Z having the standard Normal
distribution, the P-value for a test of H0 against
Ha : µ > µ0 is P (Z > z∗ )
Ha : µ < µ0 is P (Z < z∗ )
Ha : µ 6= µ0 is 2P (Z > |z∗ |)
MATH 214 (NOTES) – p. 24/6
Problem 9 (page 356)
Consider the following hypothesis test:
H0 : µ = 20
Ha : µ < 20
A sample of 50 provided a sample mean of 19.4. The
population standard deviation is 2.
a. Compute the value of the test statistic.
b. What is the p-value?
c. Using α = 0.05, what is your conclusion?
MATH 214 (NOTES) – p. 25/6
Solution
a. Test statistic.
z∗ =
x̄−µ
√0
σ/ n
=
b. P-value.
19.4−20
√
2/ 50
= −2.1213
P (Z < z∗ ) = P (Z < −2.1213) = 0.0169
c. Conclusion.
Since P-value = 0.0169 < α = 0.05, we reject H0 : µ = 20. We
conclude that µ < 20.
MATH 214 (NOTES) – p. 26/6
Problem 10 (page 357)
Consider the following hypothesis test:
H0 : µ = 25
Ha : µ > 25
A sample of 40 provided a sample mean of 26.4. The
population standard deviation is 6.
a. Compute the value of the test statistic.
b. What is the p-value?
c. Using α = 0.01, what is your conclusion?
MATH 214 (NOTES) – p. 27/6
Solution
a. Test statistic.
z∗ =
x̄−µ
√0
σ/ n
=
26.4−25
√
6/ 40
= 1.4757
b. P-value.
P (Z > z∗ ) = P (Z > 1.4757) = 0.0700
c. Conclusion.
Since P-value = 0.0700 > α = 0.01, we CAN’T reject
H0 : µ = 25. We conclude that we don’t have enough
evidence to claim that µ > 25. (Some of us would say that we
accept that µ = 25).
MATH 214 (NOTES) – p. 28/6
Problem 11 (page 357)
Consider the following hypothesis test:
H0 : µ = 15
Ha : µ 6= 15
A sample of 50 provided a sample mean of 14.15. The
population standard deviation is 3.
a. Compute the value of the test statistic.
b. What is the p-value?
c. Using α = 0.05, what is your conclusion?
MATH 214 (NOTES) – p. 29/6
Problem 11 (Solution)
a. Test statistic.
z∗ =
x̄−µ
√0
σ/ n
=
b. P-value.
14.15−15
√
3/ 50
= −2.0034
2P (Z > |z∗ |) = 2P (Z > | − 2.0034|) = 2P (Z > 2.0034) = 0.0451
c. Conclusion.
Since P-value = 0.0451 < α = 0.05, we reject H0 : µ = 15. We
conclude that µ 6= 15.
MATH 214 (NOTES) – p. 30/6
Tests from confidence intervals
CONFIDENCE INTERVALS AND TWO-SIDED TESTS.
A level α two-sided significance test rejects a hypothesis
H0 : µ = µ0 exactly when the value µ0 falls outside a level
1 − α confidence interval for µ.
MATH 214 (NOTES) – p. 31/6
Problem 11 (again)
The 95% confidence interval for µ in problem 11 is:
σ
x̄ ± z∗ ( √ )
n
3
14.15 ± 1.96( √ )
50
(13.3184, 14.9815)
The hypothesized value µ0 = 15 in problem 11 falls outside
this confidence interval, so we reject H0 : µ = 15.
MATH 214 (NOTES) – p. 32/6
Problem 23 (page 363)
H0 : µ = 12
Ha : µ > 12
A sample of 25 provided a sample mean x̄ = 14 and a
sample standard deviation s = 4.32.
a. Compute the value of the test statistic.
b. Use the t distribution table to compute a range for the
p-value.
c. At α = 0.05, what is your conclusion?
MATH 214 (NOTES) – p. 33/6
Solution
a. t∗ =
x̄−µ
√0
s/ n
=
14−12
√
4.32/ 25
= 2.31
b. Degrees of freedom = n − 1 = 24.
P-value = P (T > t∗ ) = P (T > 2.31)
Using t-table (on page 920), P-value is between 0.01 and
0.025.
Exact P-value = 0.0147 (using a TI-83 and the function
T-Test).
c. Since P-value < α = 0.05, we reject H0 .
MATH 214 (NOTES) – p. 34/6
Problem 24 (page 363)
H0 : µ = 18
Ha : µ 6= 18
A sample of 48 provided a sample mean x̄ = 17 and a
sample standard deviation s = 4.5.
a. Compute the value of the test statistic.
b. Use the t distribution table to compute a range for the
p-value.
c. At α = 0.05, what is your conclusion?
MATH 214 (NOTES) – p. 35/6
Solution
a. t∗ =
x̄−µ
√0
s/ n
=
17−18
√
4.5/ 48
= −1.54
b. Degrees of freedom = n − 1 = 47.
P-value = 2P (T > |t∗ |) = 2P (T > | − 1.54|) = 2P (T > 1.54)
Using t-table (on page 920), P-value is between 0.10 and
0.20.
Exact P-value = 0.1303 (using a TI-83 and the function
T-Test).
c. Since P-value > α = 0.05, we CAN’T reject H0 .
MATH 214 (NOTES) – p. 36/6
Another approach
Recall that α = 0.05 and that we have a two-sided alternative
(Ha : µ 6= 18) which means that we could solve this problem
using a 95% confidence interval instead of the four-step
procedure presented above.
x̂ ± t∗ ( √sn )
)
17 ± 2.012( √4.5
48
(15.6931, 18.3068)
The hypothesized value µ0 = 18 in problem 18 falls INSIDE
this confidence interval, so we CAN’T reject H0 : µ = 18.
MATH 214 (NOTES) – p. 37/6
Problem 25 (page 363)
H0 : µ = 45
Ha : µ < 45
A sample of 36 is used. Identify the p-value and state your
conclusion for each of the following sample results. Use
α = 0.01.
a. x̄ = 44 and s = 5.2.
b. x̄ = 43 and s = 4.6.
c. x̄ = 46 and s = 5.0.
MATH 214 (NOTES) – p. 38/6
Solution a
a. x̄ = 44 and s = 5.2.
P-value = P (T < t∗ ) = P (T < −1.1538) = P (T > 1.1538) (T
distributions are symmetric)
Using t-table (on page 921), P-value is between 0.10 and
0.20.
Exact P-value = 0.1281 (using a TI-83 and the function
T-Test).
Since P-value > α = 0.01, we CAN’T reject H0 .
MATH 214 (NOTES) – p. 39/6
Solution b
b. x̄ = 43 and s = 4.6.
P-value = P (T < t∗ ) = P (T < −2.6086) = P (T > 2.6086) (T
distributions are symmetric)
Using t-table (on page 921), P-value is between 0.005 and
0.01.
Exact P-value = 0.0066 (using a TI-83 and the function
T-Test).
Since P-value < α = 0.01, we reject H0 . We conclude that
µ < 45.
MATH 214 (NOTES) – p. 40/6
Solution c
c. x̄ = 46 and s = 5.0.
P-value = P (T < t∗ ) = P (T < 1.2) = 1 − P (T > 1.2) (T
distributions are symmetric)
Using t-table (on page 921), P-value is between 0.80 and
0.90.
Exact P-value = 0.8809 (using a TI-83 and the function
T-Test).
Since P-value > α = 0.01, we can’t reject H0 .
MATH 214 (NOTES) – p. 41/6
Problem 27
The Employment and Training Administration reported the
U.S. mean unemployment insurance benefit of $ 238 per
week. A researcher in the state of Virginia anticipated that
sample data would show evidence that the mean weekly
unemployment insurance benefit in Virginia was below the
national level.
a. Develop appropriate hypotheses such that rejection of H0
will support the researcher’s contention.
b. For a sample of 100 individuals, the sample mean weekly
unemployment insurance benefit was $231 with a sample
standard deviation of $80. What is the p-value?
c. At α = 0.05, what is your conclusion?.
MATH 214 (NOTES) – p. 42/6
Solution
a. H0 : µ = 238 vs Ha : µ < 238.
x̄−µ
√ 0 = 231−238
√
= −0.88
b. t∗ = s/
n
80/ 100
Degrees of freedom = n − 1 = 99.
Using t table (page 922), P-value is between 0.10 and 0.20
c. P-value > 0.05, we CAN’T reject H0 . Cannot conclude
mean weekly benefit in Virginia is less than the national
mean.
MATH 214 (NOTES) – p. 43/6
Problem 28 (page 364)
The National Association of Professional Baseball Leagues,
Inc., reported that attendance for 176 minor league baseball
teams reached an all-time high during the 2001 season. On
a per-game basis, the mean attendance for minor league
baseball was 3530 people per game. Midway through the
2002 season, the president of the association asked for an
attendance report that would hopefully show that the mean
attendance for 2002 was exceeding the 2001 level.
MATH 214 (NOTES) – p. 44/6
Problem 28 (cont.)
a. Formulate hypotheses that could be used to determine
whether the mean attendance per game in 2002 was greater
than the previous year’s level.
b. Assume that a sample of 92 minor league baseball
games played during the first half of the 2002 season
showed a mean attendance of 3740 people per game with a
sample standard deviation of 810. What is the p-value?
c. At α = 0.01, what is your conclusion?
MATH 214 (NOTES) – p. 45/6
Solution
a.H0 : µ = 3530 vs Ha : µ > 3530
x̄−µ
√ 0 = 3740−3530
√
= 2.49
b. t∗ = s/
n
810/ 92
Degrees of freedom = n − 1 = 91. Using t-table (on page
922), P-value is between 0.005 and 0.01.
Exact P-value = 0.007 (using a TI-83 and the function T-Test).
c. Since P-value < α = 0.01, we reject H0 . We conclude that
the mean attendance per game has increased.
MATH 214 (NOTES) – p. 46/6
Hypotheses Tests for a Proportion
To test the hypothesis H0 : p = p0 , compute the z∗ statistic,
z∗ =
q p̂−p0
p0 (1−p0 )
n
In terms of a variable Z having the standard Normal
distribution, the approximate P-value for a test of H0 against
Ha : p > p0 : is : P (Z > z∗ )
Ha : p < p0 : is : P (Z < z∗ )
Ha : p 6= p0 : is : 2P (Z > |z∗ |)
Use this test when the sample size n is so large that both
np0 and n(1 − p0 ) are 10 or more.
MATH 214 (NOTES) – p. 47/6
Problem 36 (page 368)
Consider the following hypothesis test:
H0 : p = 0.75
Ha : p < 0.75
A sample of 300 items was selected. Compute the p-value
and state your conclusion for each of the following sample
results. Use α = 0.05.
a. p̂ = 0.68
b. p̂ = 0.72
c. p̂ = 0.70
d. p̂ = 0.77
MATH 214 (NOTES) – p. 48/6
Solution a
z∗ = √
p̂−p0
p0 (1−p0 )/n
=√
0.68−0.75
0.75(1−0.75)/300
= −2.80
Using Normal table, P-value =
P (Z < z∗ ) = P (Z < −2.80) = 0.0026
P-value<α = 0.05, reject H0 .
MATH 214 (NOTES) – p. 49/6
Solution b
z∗ = √
p̂−p0
p0 (1−p0 )/n
=√
0.72−0.75
0.75(1−0.75)/300
= −1.20
Using Normal table, P-value =
P (Z < z∗ ) = P (Z < −1.20) = 0.1151
P-value>α = 0.05, do not reject H0 .
MATH 214 (NOTES) – p. 50/6
Solution c
z∗ = √
p̂−p0
p0 (1−p0 )/n
=√
0.70−0.75
0.75(1−0.75)/300
= −2.00
Using Normal table, P-value =
P (Z < z∗ ) = P (Z < −2.00) = 0.0228
P-value<α = 0.05, reject H0 .
MATH 214 (NOTES) – p. 51/6
Solution d
z∗ = √
p̂−p0
p0 (1−p0 )/n
=√
0.77−0.75
0.75(1−0.75)/300
= 0.80
Using Normal table, P-value =
P (Z < z∗ ) = P (Z < 0.80) = 0.7881
P-value>α = 0.05, do not reject H0 .
MATH 214 (NOTES) – p. 52/6
Problem 35 (page 368)
Consider the following hypothesis test:
H0 : p = 0.20
Ha : p 6= 0.20
A sample of 400 provided a sample proportion p̂ = 0.175.
a. Compute the value of the test statistic.
b. What is the p-value?
c. At the α = 0.05, what is your conclusion?
d. What is the rejection rule using the critical value? What is
your conclusion?
MATH 214 (NOTES) – p. 53/6
Solution
a. z∗ =
q p̂−p0
p0 (1−p0 )
n
=
0.175−0.20
q
(0.20)(0.80)
400
= −1.25
b. Using Normal table, P-value = 2P (Z > |z∗ |) = 2P (Z >
| − 1.25|) = 2P (Z > 1.25) = 2(0.1056) = 0.2112
c. P-value > α = 0.05, we CAN’T reject H0 .
MATH 214 (NOTES) – p. 54/6
Problem 37 (page 369)
A study found that, in 2005, 12.5% of U.S. workers belonged
to unions. Suppose a sample of 400 U.S. workers is
collected in 2006 to determine whether union efforts to
organize have increased union membership.
a. Formulate the hypotheses that can be used to determine
whether union membership increased in 2006.
b. If the sample results show that 52 of the workers
belonged to unions, what is the p-value for your hypothesis
test?
c. At α = 0.05, what is your conclusion?
MATH 214 (NOTES) – p. 55/6
Solution
a. H0 : p = 0.125 vs Ha : p > 0.125
52
= 0.13
b. p̂ = 400
z∗ =
q p̂−p0
p0 (1−p0 )
n
=
q0.13−0.125
(0.125)(0.875)
400
= 0.30
Using Normal table, P-value =
P (Z > z∗ ) = P (Z > 0.30) = 1 − 0.6179 = 0.3821
c. P-value = > 0.05, do not reject H0 . We cannot conclude
that there has been an increase in union membership.
MATH 214 (NOTES) – p. 56/6
Problem 38 (page 369)
A study by Consumer Reports showed that 64% of
supermarket shoppers believe supermarket brands to be as
good as national name brands. To investigate whether this
result applies to its own product, the manufacturer of a
national name-brand ketchup asked a sample of shoppers
whether they believed that supermarket ketchup was as
good as the national brand ketchup.
MATH 214 (NOTES) – p. 57/6
Problem 38 (cont.)
a. Formulate the hypotheses that could be used to
determine whether the percentage of supermarket shoppers
who believe that the supermarket ketchup was as good as
the national brand ketchup differed from 64%.
b. If a sample of 100 shoppers showed 52 stating that the
supermarket brand was as good as the national brand, what
is the p-value?
c. At α = 0.05, what is your conclusion?
MATH 214 (NOTES) – p. 58/6
Solution
a. H0 : p = 0.64 vs Ha : p 6= 0.64
52
= 0.52
b. p̂ = 100
z∗ =
q p̂−p0
p0 (1−p0 )
n
=
q0.52−0.64
(0.64)(0.36)
100
= −2.50
Using Normal table, P-value = 2P (Z > |z∗ |) = 2P (Z >
| − 2.50|) = 2P (Z > 2.50) = 2(0.0062) = 0.0124
c. P-value = < 0.05, reject H0 . Proportion differs from the
reported 0.64.
MATH 214 (NOTES) – p. 59/6
Problem 39 (page 369)
The National Center for Health Statistics released a report
that stated 70% of adults do not exercise regularly. A
researcher decided to conduct a study to see whether the
claim made by the National Center for Health Statistics
differed on a state-by-state basis.
a. State the null and alternative hypotheses assuming the
intent of the researcher is to identify states that differ from
70% reported by the National Center for Health Statistics.
b. At α = 0.05, what is the research conclusion for the
following states:
Wisconsin: 252 of 350 adults did not exercise regularly.
California: 189 of 300 adults did not exercise
regularly.
MATH 214 (NOTES) – p. 60/6
Solution
a. H0 : p = 0.70 vs Ha : p 6= 0.70
252
= 0.72
b. Wisconsin p̂ = 350
z∗ =
q p̂−p0
p0 (1−p0 )
n
=
q0.72−0.70
(0.70)(0.30)
350
= 0.82
Using Normal table, P-value = 2P (Z > |z∗ |) = 2P (Z > |0.82|) =
2P (Z > 0.82) = 2(0.2061) = 0.4122
c. P-value = > 0.05, do not reject H0 .
MATH 214 (NOTES) – p. 61/6
TO BE CONTINUED...
MATH 214 (NOTES) – p. 62/6