* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download The SIR Model - School of Geography
Brucellosis wikipedia , lookup
Chagas disease wikipedia , lookup
Oesophagostomum wikipedia , lookup
Hospital-acquired infection wikipedia , lookup
Onchocerciasis wikipedia , lookup
Marburg virus disease wikipedia , lookup
Sexually transmitted infection wikipedia , lookup
Coccidioidomycosis wikipedia , lookup
Eradication of infectious diseases wikipedia , lookup
Neglected tropical diseases wikipedia , lookup
Schistosomiasis wikipedia , lookup
Leptospirosis wikipedia , lookup
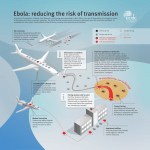
Disease Modelling: a teacher’s guide. This guide accompanies online materials introducing Agent-Based Modelling in Geography, using the modelling of diseases. The materials are for a broad range of ages and this teacher’s guide includes ideas for targeting specific key stages. The materials would additionally be suitable for use within IT teaching or a coding club working at a relatively high level with the Scratch environment. The materials can be found at: http://www.geog.leeds.ac.uk/courses/other/disease-modelling/ Key ideas Models are a key tool in understanding our world. Models are physical, mathematical, or computer-based reproductions of some part of a natural or human system. Modelling a system allows us to test how well our ideas about how things work actually generate systems that look like they do in the real world (validation of our theories). They also allow us to experiment with management plans and predict the future based on our understanding. Older models tend to be mathematical equations because these deal with lots of things that are individual objects in the real world very efficiently by aggregating them into a single number. However, what these often miss is the importance of geography; space, the time it takes to travel across it, and the position of things within it, has a complicated effect on systems that is lost if we treat everything like it is all lumped together. Now computers are more powerful, we are starting to see the rise of Agent-Based Models, which treat objects as if they are individual things that can be tracked around a system and interact with each other. These models allow us to put the geography back in, and get more accurate modeling results. These models are of increasing importance in lots of areas of geography worldwide. In the materials, using disease spread as an example, we’ll see the extra detail that these models allow by adding geography, and we’ll also see that building them is relatively simple. Why do we model diseases? Traditionally disease modelling has been used in policy planning to determine the costto-benefit ratios associated with alternative policy options. More advanced models have additionally been used to look at the levels of immunisation necessary in a population to reduce the likelihood of epidemics breaking out. As you’ll see if you play with the model, it is not necessary for everyone to be immunised to reduce this likelihood, as the chance a disease will spread through a whole population can be considerably reduced without complete immunisation of everyone (this idea, for example, played out when people were refusing the MMR vaccine – they were not simply putting their children at risk, but were putting everyone at risk of an epidemic, including those too young to be vaccinated). In general there are four strategies for dealing with a disease before it breaks out: 1) Do nothing. 2) Immunise those at risk of harm (as we do, for example, with Flu jabs). 3) Immunise enough of the susceptible population to remove the risk of epidemics, even though it is likely the disease still remains in the environment or population (as we do with MMR). 4) Immunise enough of the population to kill off the disease (as we have with Smallpox) Which we do depends on cost, potential harm, and how widely the disease exists in the population or within the environment. In most cases, several of the above will be hit at once (so, for example, MMR jabs seek to eradicate the diseases, but also protect the susceptible population). Decision making can be quite complicated, so, for example, the UK government has decided not to immunise cattle against Foot and Mouth disease because of trade restrictions that are founded (in part) on the idea that immunisation could potentially hide small populations of unimmunised asymptomatic carriers (animals that carry the disease but without any ill effects), which could then be sold on the international market causing epidemics elsewhere. During an epidemic, the options for immunisation are reduced because it is difficult to store large stocks of immunisations indefinitely or produce them quickly. Policy therefore often centres on controlling movement and infection spread. With humans this may range from isolation wards to warnings to stay at home if infected, but with animals and plants this may stretch from trade and movement restrictions through to culling. In all these policy areas, models can help in the decision making process by assessing the likely speed and size of disease spread, and the amount of potential harm. Models can also be used to look at past diseases in a research context and determine attributes of the diseases like the infectiousness. How do we model the spread of disease? The SIR Model The Susceptible-Infected-Recovered (or sometimes “Removed”) (SIR) model is used in epidemiology to calculate the number of susceptible, infected and recovered people within a population. It can be used, for example, to estimate the number of people needing medical attention during an epidemic. The model was first proposed by Kermack and McKendrick in 1927. It is known as a compartmental model as it divides the population into three broad categories. Diagrammatically, the model is given in Figure 1: Figure 1: Diagrammatic representation of the SIR model. Table 1 gives the terms that are used within the model: Term Definition Susceptible (S) Can be infected Infected (I) Has the disease Recovered (R) Has built up immunity to the disease or has died Infection Rate (r) The number of people becoming infected Recovery rate (a) The number of people recovering Table 1: Main terms used within the SIR model. Nearly all individuals in the population are Susceptible (with the exception of those who could be immune). Once an individual has the disease, they move from Susceptible to Infected. As they recover, they move from Infected to Recovered. When R = “Removed”, then people in the “R” category can be recovered or dead; either way they can’t be re-infected. In general the SIR model is run mathematically. This is fine as long as the infection rate is well known; however, in general this is not true. It may be estimated from previous epidemics, but such estimates are poor when either transport or migration types are changing, or where these estimates are made based on one culture/country but are then transferred to another. What is missing from this is the geography of human interactions. Agent-Based Modelling In general people use aggregate mathematical models where they can’t cope with trying to understand individual-level issues. So, for example, economic predictions of inflation generally work by taking into account several aggregated figures representing potential influences, rather than trying to model every single person trading in/with a country and the prices they want to sell goods at. For 3000 years this approach has done us well, but it has two issues: 1) It fails to do a completely accurate job of modelling systems (so we tend to rely on error statistics to help us understand how bad a job the models are doing). For example, there are some mechanisms (like decision making) that are poorly represented by maths. 2) It makes us think of people as an aggregate, and concentrates on the big patterns, rather than concentrating on the lived experience of people and how the big patterns are generated in the real world. Fortunately, with the rise of computing power and the easy availability of individual-level data about the world, it has recently become much easier to model systems by starting with individuals and their behaviour and seeing how these complex systems (that is, systems of complicated, often non-linear interactions) produce emergent patterns (that is patterns at the large scale you wouldn’t necessarily be able to predict by looking at the individuals’ behaviour one at a time). One of the chief techniques for doing this is Agent-Based Models (ABM). In an ABM, individuals are represented as independent software “agents” within a computer environment, each with their own set of attributes and behaviours. The environment can be something abstract (like a rectangular space) or something more realistic (like a map of a country). The agents are allowed to interact with the environment and each other to see what patterns are generated. Each agent is just a chunk of software code that records what it is doing and does stuff with other bits of computer code. You’ll see how to build an ABM in the materials – the “Scratch” software, free and widely used in primary and secondary schools, makes it very easy. Agent-based modelling of diseases Plainly, then, this ability to model individuals, their locations, and who they interact with, sounds like the kind of thing that is missing from the SIR models. If we can make a model that includes people’s movements and social interactions, be that going down the shops or flying internationally, we could work out the likelihood of infection much more accurately for specific contexts. Not only that, but we could model how changes to movements might stop disease spread. For example, during the outbreak of swine flu, it was fast realised that stopping international travel was pointless (the disease had already spread internationally through key, quick moving, travellers), however, local contagion could be slowed or prevented by asking victims to stay at home if they were able to do so. Without understanding the detailed dynamics of travel, much effort could have been incorrectly invested. In addition, models with more realistic geography and movements give a much better appreciation of potential spatial spread and therefore variation in levels of harm. This is particularly important where some populations may be immune because they have suffered previous diseases that have removed susceptible people in the population (currently or through the disease having affected ancestral populations). Key in all this is the geography: where people are, the resources they have access to, and the cultures they form. Geographers therefore have an increasingly key role to play in understanding and controlling diseases. Here we are looking at infectious diseases, but this goes equally for diseases resulting from living conditions or lifestyles, as both of these also relate to where people are, and the opportunities they have in those spaces. The model The model presented in these materials is a very simple replication of the SIR model, but with some added geography and movement. The geography is very simple (a rectangular space) and the movements are random. However, even with this simple model, students can explore the fundamental issues associated with disease spread and the importance of geography and movements within a geography. The model has three options: 1) The ratio of susceptible to immune people at the start, essentially replicating S, above. 2) The length of time infectious, which is also taken as the infected period. 3) The result of the infections (death vs. immunity), which isn’t so important for the spread in SIR models, but becomes important for harm calculations and for diseases where victims don’t become immune). Questions The material asks various questions. One option would be to get students to work around a computer in groups and use the questions as discussion points. Here are some brief ideas of answers. What kinds of things are important in controlling the spreading rate in the model? The disease will generally spread slowly if at all unless people are close. Things that control it include the spread of people and the number of people, i.e. the density of people. The speed people move will also have an effect. What kinds of things might be important in the real world? The control by the density of people is much as you might expect in the real world. Of course in the real world people don’t move randomly, but also some situations are more conducive to infection than others, so being stuck with someone in a train carriage is very different to being stuck with them in a field even if you are the same distance apart. In the real world in some countries people can plainly get in a car and move very fast from one side of an area to another, meaning that long-distance trips can spread infection quite rapidly and open up disease pockets on the other side of an area. We see this, for example, with Foot and Mouth, where local infections spread out from individuals a bit like this model, but long distance cattle movements can spark off multiple new local infections. How does this relate to, for example, how the government deals with potentially deadly diseases in cattle like Foot and Mouth? Foot and Mouth is an interesting disease, because it seems to spread through the air reasonably well. This means that generally the government takes two approaches to it. They stop the movement of cattle between areas to prevent cow-to-cow contact, but also cull uninfected cattle in farms surrounding infections to prevent local spread. In general what the government does by culling is accelerate the process through infection to death, reducing the amount of time spent infectious (see below). It is hard to imagine this ever being possible with a human disease (hard, but not impossible!). How does the speed to death affect the spread of the disease? In general diseases that kill quickly, although horrible for individuals, are less dangerous for populations than those that kill slowly/have a long infection. Obviously people who die before they can transmit the disease are less dangerous than people who stumble around giving lots of others a disease before they finally die. Are real-world diseases (like Ebola) that spread very rapidly and kill all their victims likely to be the most dangerous kinds of diseases in terms of most deaths? The above is why, in general, Ebola doesn’t produce epidemics. It tends to break out in areas of low population density and kills very quickly. So, while it is extremely infectious, the opportunities for infection are low. Of course, as has been seen recently, once it reaches high density populations, it becomes much more problematic. One of the worries with current SARS-like and Flu diseases with high mortality, is that they have a longer period during which infected individuals are mobile and/or don’t show any symptoms. What kinds of effects to these different options have? By and large, the higher the ratio of immune people, given the same density and population, the slower the disease spread. The faster the disease progresses, the less time there is for infectious contact. The recovery type (immune/dead) has no effect on transmission rates. However, deaths obviously have an impact on cost-harm analyses. What settings would you give these options for the following diseases: Measles: Low susceptibility(?); medium infectious time; low rate of deaths. Colds: High susceptibility; high infectious time; very low rate of deaths. SARs: High susceptibility; high infectious time; medium/high rate of deaths. Students may like to go through the Wikipedia pages and try to work out exact figures. Given the people here move randomly and real people don't, do you think immunity will be more or less important in the real world? In real social interactions immunity would probably be more important. In terms of initial spread of the disease it lowers infection probabilities if the people you talk to day to day are immune. In terms of recovery vs. death, it might be important for spreading rates if deaths pushed people into contact with infected people doing jobs immune people might otherwise do. Say each infected person infects another at a rate of one a second, and newly infected people can infect other people as well, what kind of graph might we expect for such a model? We would normally expect a roughly geometric progression in infection rates and total people infected (students can try this in Excel). Why don't we get this graph in practice? Because this assumes there will always be someone to infect. Not only isn’t this true, but it becomes less true as the stock of people is exhausted, theoretically leading to the graph plateauing. How might this be reflected in the infection rate in a real disease, and how might we control real diseases? Obviously the quicker we can isolate people with the disease the less people infected there will be to spread the disease. Other possible questions for Students: What else could be added to this model to make it more realistic? Things that are different in the real world compared with the model for more general discussion: 1) Obviously people don’t randomly move around. 2) People aren’t always infectious when infected, so this element needs splitting. 3) People aren’t always symptomatic, even if they are infectious (the most notorious example being Typhoid Mary, see http://en.wikipedia.org/wiki/Asymptomatic_carrier and linked pages). 4) Some diseases don’t result in immunity. 5) Some diseases are picked up from the environment, or the environment acts as a reservoir for diseases that initially start in humans (see, for example, the classic case of Dr Snow and the Broad Street cholera outbreak: http://en.wikipedia.org/wiki/John_Snow_%28physician%29#Cholera ). How could scientists use this model? They could use it to study the effects on a population under different diseases; for example, diseases with different levels of contagiousness. The materials There are two options for the materials. One is working through the above issues around diseases using a model already built in Processing (http://processing.org/) and built into the web pages. The other, which concentrates on getting hands-on experience of building these models, and showing that they aren’t beyond anyone, involves building a model within Scratch (http://scratch.mit.edu/). The latter would also be suitable for advanced Scratch users within an IT course or coding club. We also provide an Excel SIR model for comparison (see Appendix A for some materials for use with this). Possible lesson plans: All Key Stages All Key Stages could probably happily work through the materials on the pre-built model. It may be worth choosing a specific disease from the outset to avoid dwelling on terrifying diseases like Ebola with some classes. Classes could be split into groups of two or three to work through the model and answer the questions. Core issues outside of the materials that might be raised include the degree to which modern culture makes us more or less susceptible to rapid disease spread, whether the trade-off is good, and whether some cultures would be more or less resilient. In addition, the model may be of use in tackling issues of the spread of culture and ideas. Compare and contrast, for example, the issue of Meme Spread. Key Stage 5 Key Stage 5 students should be able to work through the Scratch tutorial and think about how they would develop a more realistic model. Students with an IT programming training could have a go at implementing the model in alternative languages, but more realism can be added to the model within Scratch. Some alternative models are given in Appendix B, but the questions above should also introduce alternative changes that could be made. Alternative lesson plans might look at some of the literature resources outlined below and talk about the uses of simulation, both within disease modelling and geography more broadly. One interesting area (and one we are currently investing a lot of energy in) is Crime Prediction. We build models of cities and then simulate burglars within them to see where they might commit crimes. For more information, see Nick Malleson’s Blog, at: http://nickmalleson.co.uk/blog/ Further resources Articles and books Anderson, R. M. ed. (1982) Population Dynamics of Infectious Diseases: Theory and Applications, Chapman and Hall, London-New York. Anderson, R. M. & May, R. M. (1991). Infectious Diseases of Humans. Oxford: Oxford University Press. Kermack, W.O., and A. G. McKendrick. 1927. A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society of London 115:700-721. May, R. M. (1976). "Simple mathematical models with very complicated dynamics". Nature 261 (5560): 459–467 A few real world examples: Ball F., and Lyne O. (2006) Optimal vaccination schemes for epidemics among a population of households, with application to variola minor in Brazil. Stat Methods Med Res. 2006 Oct;15(5):481-97. [online] http://smm.sagepub.com/content/15/5/481.full.pdf+html Dion, E., VanSchalkwyk, L., and Lambina, E.F. (2011) The landscape epidemiology of foot-and-mouth disease in South Africa: A spatially explicit multi-agent simulation. Ecological Modelling Volume 222, Issue 13, 10 July 2011, Pages 2059–2072 [online] http://www.sciencedirect.com/science/article/pii/S0304380011001499 Teruhiko Yoneyama, T. and Krishnamoorthy, M.S. (2011) Simulating the spread of influenza pandemic of 2009 considering international traffic. Simulating the spread of influenza pandemic of 2009 considering international traffic [online] http://sim.sagepub.com/content/88/4/437.abstract?etoc Articles for students Coppola, K. (2007) Virtual outbreaks, real world ramifications. New Scientist 2592 [online] http://www.newscientist.com/article/mg19325921.700-virtual-outbreaks-realworld-ramifications.html Ghosh, P. (2009) Science ponders 'zombie attack' BBC News Online [online] http://news.bbc.co.uk/1/hi/8206280.stm Munz, P., Hudea, I., Imad, J., and Smith?, R.J. (2009) When Zombies Attack!: Mathematical Modelling Of An Outbreak Of Zombie Infection. In: Tchuenche, J.M., and Chiyaka, C. (eds) Infectious Disease Modelling Research Progress. Nova Science Publishers, Inc. [online] http://mysite.science.uottawa.ca/rsmith43/Zombies.pdf Manjoo, F. (2013) Bigger, Better, Even More Crazily Addictive [SimCity as an ABM] Slate [online] http://www.slate.com/articles/technology/technology/2013/03/simcity_review_the_ne w_version_of_the_classic_game_is_totally_addictive.html Websites: Our website: http://mass.leeds.ac.uk/ Nick Malleson’s Blog on ABM in Geography, especially Crime Prediction: http://nickmalleson.co.uk/blog/ Basic information from Wikipedia: http://en.wikipedia.org/wiki/Epidemic_model World Health Organisation (including links to videos and fact sheets): http://www.who.int/topics/infectious_diseases/en/ The Infectious Disease Institute at Cambridge has a set of useful resources: http://www.infectiousdisease.cam.ac.uk/schoolzone/learning-resources Disease in Crusader Latrines: http://www.cam.ac.uk/research/features/the-worm-thatturned-east/ School Science: http://www.schoolscience.co.uk/ Lots of additional resources. Information on a range of infectious diseases: http://www.abpischools.org.uk/page/modules/diseases/diseases1.cfm?coSiteNavigatio n_allTopic=1 Appendix A: Materials for use with the Excel spreadsheet model Consider the situation if one individual becomes ill in your class, how long do you think that it would take to spread through the class? What would we need to know in order to find out? How many people are in the class? TOTAL = 35 (students give actual number) How many people are infected? INITIAL INFECTED = 1 (students can guess) How many people are susceptible (i.e. not ill yet, but could be)? SUSCEPTIBLE = TOTAL – INFECTED Therefore, those who are not infected must be well BUT susceptible to getting sick. By building the basic components of the SIR model into the model, we can see what happens to individuals when a disease spreads. Experiment with the number of initially infected people. Does the disease spread more quickly? While the SIR model can tell us the infection rates, it doesn’t tell who was infected and where they were. We can use the model to tell us how quickly the disease is spreading. Experiment with this now and think about why this type of information would be useful. Optional: A simple Excel spreadsheet has been made for you to play around with different susceptible and infected populations. The SIR model To understand how this simulates the spread of disease through a population, we need to think about a few things. First, how do we work out how many people will become ill each day? To do this, we need to calculate the number of possible interactions between the infected and susceptible individuals. We do this by calculating infection rates by taking the following steps: How many interactions between susceptible and infected? Possible interactions = S * I Actual interactions = Possible * Interaction Rate Infectious Interactions = Actual * Infection Rate Delta infected = S * I * Interaction Rate * Infection Rate Interaction rate = % people you interact with Infection rate = % interactions that result in infection [Can play around with these variables in the Excel spreadsheet] This is still rather simplistic; we need to add more detail to make it more realistic. There are a couple of immediate improvements that we can make by taking account of the following: The time until infected person dies or recovery The probability that an individual will die % of immunity in a population (i.e. some individuals will never get sick) You can play around with these options and see what happens to the population in the. Assumptions of the SIR model While useful, this model only works with the following assumptions: The population is fixed (no births or deaths) The only way a person can leave the susceptible group is to become infected. The only way a person can leave the infected group is to recover or die from the disease. Once recovered, the individual is immune from the disease. Age, sex, ethnicity and social status have no affect on the likelihood of being infected. There is no inherited immunity. All members of the population have the same number of interactions. As a result of these assumptions, the SIR model cannot be applied to all diseases. For example, it would be difficult to model colds using this model: in general we may become immune to a specific cold having had it, but the number of different cold viruses is so large that the chance of getting another is high, and we tend to think of colds as not having a recovered immunity associated with them, especially in young populations. Appendix B: Other extensions to the SIR model While the SIR is one of the most commonly used models, it cannot be applied to all diseases. Below are two other models that you may wish to create in Scratch and play around with. Susceptible – Exposed-Infected-Recovered model Figure 2 shows the SEIR model. For many infections, such as Chicken Pox, there is a period of time where the individual is infected BUT not infectious. Here, we say that they have been exposed. It’s important to know about these individuals if we are to fully understand who maybe infected and where the disease may spread. Figure 2: The SEIR model The Susceptible Infectious model Whereas most diseases, once recovered, give the individual some immunity (Chicken Pox), there are a group of diseases that do not. There is no recovered stage here as once the individual is well again, there is no immunity and they are immediately susceptible again. This is known as the Susceptible-Infectious model and is shown in Figure 3. Figure 3: Susceptible – Infectious model.