* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Constant-Time LCA Retrieval
Computational phylogenetics wikipedia , lookup
Exact cover wikipedia , lookup
Sieve of Eratosthenes wikipedia , lookup
Signal-flow graph wikipedia , lookup
Path integral formulation wikipedia , lookup
Travelling salesman problem wikipedia , lookup
Selection algorithm wikipedia , lookup
Constant-Time LCA Retrieval
Presentation by Danny Hermelin,
String Matching Algorithms Seminar,
Haifa University.
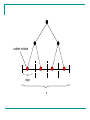
The Lowest Common Ancestor
In a rooted tree T, a node u is an ancestor of
a node v if u is on the unique path from the
root to v.
In a rooted tree T, the Lowest Common
Ancestor (LCA) of two nodes u and v is the
deepest node in T that is the ancestor of both
u and v.
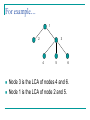
For example…
1
2
3
4
5
6
Node 3 is the LCA of nodes 4 and 6.
Node 1 is the LCA of node 2 and 5.
The LCA Problem
The LCA problem is then, given a rooted tree T for
preprocessing, preprocess it in a way so that the
LCA of any two given nodes in T can be retrieved
in constant time.
In this presentation we shall present a
preprocessing algorithm that requires no more
then linear time and space complexity.
The assumed machine model
We make the following two assumptions on our
computational model.
Let n denote the size of our input in unary representation:
All arithmetic, comparative and logical operations on
numbers whose binary representation is of size no more
then logn bits can be done in constant time.
We assume that finding the left-most bit or the right-most
bit of a logn sized number can be done in constant time.
The first assumption is a very reasonable
straightforward assumption considering most
machines on the market today.
The second seems less reasonable but can be
achieved with the help of a few (constant numbered)
tables of size O( n ).
These assumptions helps our discussion focus on the
more interesting parts of the algorithm solving the LCA
problem.
The Simple case:
Complete Binary Tree
Our discussion begins with a particularly simple
instance of the LCA problem, LCA queries on
complete binary trees.
We will use our knowledge of solving the LCA
problem on complete binary trees and expand it
later on, to solve the LCA problem on any arbitrary
rooted tree T.
Let B denote a complete binary tree with n
nodes.
The key here is to encode the unique path from
the root to a node in the node itself. We assign
each node a path number, a logn bit number
that encodes the unique path from the root to the
node.
The Path Number
For each node v in B we encode a path number in
the following way:
Counting from the left most bit, the i’th bit of the path
number for v corresponds to the i’th edge on the path from
the root to v.
A 0 for the i’th bit from the left indicates that the i’th edge
on the path goes to a left child, and a 1 indicates that it
goes to a right child.
Let k denote then number of edges on the path from the
root to v, then we mark the k+1 bit (the height bit) of the
path number 1, and the rest of the logn-k-1 bits 0.
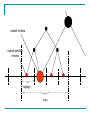
For example…
1
0
node j
1
0
0
node i
Node i’s path number is
Node j’s path number is
0101
1010
The height bit is marked in blue
Padded bits are marked in red.
1000
0100
0010
0001
1100
0110
0011
0101
1010
0111 1001
1011
1110
1101
1111
Path numbers can easily be assigned in a
simple O(n) in-order traversal on B.
How do we solve LCA queries in B
Suppose now that u and v are two nodes in B, and
that path(u) and path(v) are their appropriate path
numbers.
We denote the lowest common ancestor of u and v
as lca(u,v).
We denote the prefix bits in the path number, those
that correspond to edges on the path from the root,
as the path bits of the path number.
First we calculate path(u) XOR path(v) and find the
left most bit which equals 1.
If there is no such bit than path(u) = path(v) and so
u = v, so assume that the k’th bit of the result is 1.
If both the k’th bit in path(u) and the k’th bit in
path(v) are path bits, then this means that u and v
agree on k-1 edges of their path from the root,
meaning that the k-1 prefix of each node’s path
number encodes within it the path from the root to
lca(u,v).
For example…
lca(u,v)
u
0100
0010
v
0111
path(u) XOR path(v) =
0010
XOR
0111
0101
path(lca(u,v) =
0 1 0 0
height bit
padded bits
For example…
lca(u’,v’)
1010
u’
1001
v’
1011
path(u’) XOR path(v’) =
1001
XOR
1011
0010
path(lca(u,v) =
1 0 1 0
height bit
padded bit
This concludes that if we take the prefix k-1 bits
of the result of path(u) XOR path(v), add 1 as
the k’th bit, and pad logn-k 0 suffix bits, we get
path(lca(u,v)).
If either the k’th bit in path(u) or the k’th bit in
path(v) (or both) is not a path bit then one node
is ancestor to the other, and lca(u,v) can easily
be retrieved by comparing path(u) and path(v)’s
height bit.
The general LCA algorithm
The following are the two stages of the general
LCA algorithm for any arbitrary tree T:
First, we reduce the LCA problem to the
Restricted Range Minima problem. The
Restricted Range Minima problem is the problem
of finding the smallest number in an interval of a
fixed list of numbers, where the difference between
two successive numbers in the list is exactly one.
Second, we solve the Restricted Range Minima
problem and thus solve the LCA problem.
The Reduction
Let T denote an arbitrary tree
Let lca(u,v) denote the lowest common ancestor
of nodes u and v in T.
First we execute a depth-first traversal of T to label
the nodes in the depth-first order they are
encountered.
In that same traversal we maintain a list L, of
nodes of T, in the same order that they were
visited.
The only property of the depth-first numbering we
need is that the number given to any node is
smaller then the number given to any of it’s
descendents.
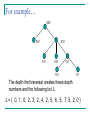
For example…
000
001
010
011
100
101
110
111
The depth-first traversal creates these depth
numbers and the following list L:
L = { 0, 1, 0, 2, 3, 2, 4, 2, 5, 6, 5, 7, 5, 2, 0 }
Now if want to find lca(u,v), we find the first
occurrence of the two nodes in L, this defines an
interval I in L.
Suppose u occurs in L before v. Now, I describes
the part of the traversal, from the point we first
discovered u to the point we first discovered v.
lca(u,v) can be retrieved by finding the minimum
number in I.
This is due to the following two simple facts:
If u is an ancestor of v then all those nodes visited
between u and v are in u’s subtree, and thus the
depth-number assigned to u is minimal in I.
If u is not an ancestor of v, then all those nodes
visited between u and v are in lca(u,v)’s subtree,
and the traversal must visit lca(u,v). Thus the
minimum of I is the depth-number assigned to
lca(u,v).
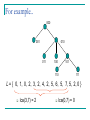
For example..
000
001
010
011
100
101
110
111
L = { 0, 1, 0, 2, 3, 2, 4, 2, 5, 6, 5, 7, 5, 2, 0 }
lca(3,7) = 2
lca(0,7) = 0
The Restricted Reduction
So far we’ve shown how to reduce the LCA problem
to the range minima problem. This next step shows
how to achieve reduction to the restricted range
minima problem.
Denote level(u) as the number of edges in the
unique path from the root to node u in T.
If L = { l1, l2, … , lz } then we build the following list :
L’={level(l1),level(l2),…level(lz)}.
We use L’ in the same manner we used L in the
previous reduction scheme.
This works because in every interval I = [u,v] in L,
lca(u,v) is the lowest node in I for the same reasons
mentioned earlier.
The difference between two adjacent elements in L’
is exactly one.
This completes the reduction to the restricted range
minima problem.
The reduction complexity.
Denote n as the number of nodes in T.
Depth-first traversal can be done in O( n ) space and time
complexity.
L is of size O( n ) and thus it’s creation and initialization can be
done in O( n ) space and time complexity.
To find lca(u,v) we need the first occurrence of u and v in L. This
could be stored in a table of size O( n ). Thus the creation and
initialization of this table can be done in O( n ) space and time
complexity.
The total space and time complexity of the reduction is then
O( n ).
The Range Minima Problem
The Range Minima problem is the problem of finding
the smallest number in an interval of a fixed list of
numbers.
The Restricted Range Minima problem is an
instance of the Range Minima problem where the
difference between two successive numbers is
exactly one.
More Formally…
The Restricted Range Minima problem is stated
formally in the following:
Given a list L = { l1 , l2 , … , ln } of n real numbers,
where for each i = 1… n-1 : | li - li+1 | = 1, preprocess
the list so that for any interval [ li , li+1 , … , lj ] ,
1 i < j n, the minimum over the interval can be
retrieved in constant time.
Two preprocessing methods for the Range
Minima Problem…
The algorithm for solving the Range Minima
problem uses two preprocessing methods:
Procedure I uses no assumptions regarding the
difference between adjacent elements, and requires
O(nlogn) space and time complexity.
Procedure II uses the restricted assumption regarding
adjacent elements, and requires exponential space
and time complexity.
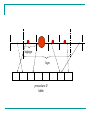
Procedure I
Suppose that our list L is of size n, and for
convenience purposes suppose n is a power of 2.The
procedure has two main stages:
First, build a complete binary tree B of size 2n-1 with n
leaves. Then for i from 1 to n, record the i’th element of L
at leaf i.
Second, for each internal node (not a leaf) in B, maintain a
suffix-list and a prefix-list containing all prefix minima and
suffix minima with respect to the leaves in it’s subtree.
Let |Lv| denote the number of nodes in the subtree
rooted by node v which is internal in B.
A prefix list of an internal node v in B is a list of size equal
to the number of leaves in v’s subtree. The k’th entry in the
list is then the smallest number among the numbers
represented by the first consecutive k leaves in v’s
subtree.
Likewise, a suffix list of v has the same size and the k’th
entry in it contains the smallest number among the
numbers represented by the last consecutive |Lv| - k +1
leaves in v’s subtree.
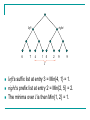
For Example…
Suppose L = { 6, 7, 4, 1, 5, 2, 9, 9}
Then Procedure I builds the following complete
binary tree for L:
6
7
4
1
5
2
9
9
6
7
4
1
5
2
9
9
The prefix list of the root node is then :
{ 6, 6, 4, 1, 1, 1, 1, 1 }
In the same manner, it’s suffix list is :
{ 1, 1, 1, 1, 2, 2, 9, 9 }
Finding the Range Minima
After the preprocessing stages are complete, the
smallest number in any interval [u,v] can be found in
constant time as follows:
First find the LCA of u and v and call it z. Recall, we
already know how to answer LCA quarries in complete
binary trees, in constant time.
The minima is then the minimum between the value of z’s
left child’s suffix list at entry u, and z’s right child’s prefix list
at entry v.
For Example…
Suppose I = { 4, 1, 5, 2 }.
The endpoints of I, 4 and 2, are leaves in B who’s LCA is
the root node.
Denote the root’s left son as left and the root’s right son
as right.
Leaf 4 is then,the third leaf from the left in left’s subtree
and leaf 2 is the second leaf from the left in right’s
subtree.
right
left
6
7
4
1
5
2
9
9
I
left’s suffix list at entry 3 = Min{4, 1} = 1.
right’s prefix list at entry 2 = Min{2, 5} = 2.
The minima over I is then Min{1, 2} = 1.
Procedure I clearly requires O(nlogn) time and
space complexity. This is a result of these two
simple facts:
The total size of all the prefix and suffix lists of all
the internal nodes of B is O(nlogn).
Each entry in these list requires constant time to
calculate if we use simple dynamic programming
techniques.
Procedure II
Procedure II use’s the assumption that the
difference between any two adjacent elements
of L is exactly one. We assume without loss of
generality that the first element of L is zero
(since, otherwise, we can subtract from every
element in L the value of the first element, and
then add it to the range-minima result).
The procedure runs in two main stages:
First, a table is built with 2n-1 entries in it. Each
entry in this table represents a valid instance of L,
and is a reference to a particular subtable.
Second, in each subtable we store the answer to
each of the n(n-1)/2 possible range queries.
All the possible instances of L are enumerable,
and so are all the range-minima queries, thus,
given an instance of L, any range-minima query
on this L can be answered in constant time.
main table
2
n-1
query
table
n
n
It is easy to see then, that Procedure II uses
n
O( 2 n 2 ) space and time complexity.
We shall now demonstrate how with the use
of Procedure I and Procedure II we achieve
linear time and space preprocessing in order
to answer all range-minima queries on L.
The Restricted Range-Minima
preprocessing algorithm
Our algorithm runs in three stages:
1.
First we partition L into logn sized subsets,
giving us a total of n/logn subsets of this kind.
We apply Procedure I to an array of all the
minimums of these subsets.
subset minima
logn
n
2.
Furthermore, each subset of size logn we
partition into smaller subsets of size loglogn
giving us logn/loglogn partitions in each
subset. Again we apply Procedure I to an array
of all the minimums of these loglogn partitions.
subset minima
subset partition
minima
loglogn
logn
3.
Finally, we run Procedure II to build the
table required for any array of size loglogn.
For each subset partition we identify it’s
proper entry in our table.
loglogn
logn
procedure II
table
After these stages are completed any range-minima
query on L, can be answered in constant time. Consider
a query requesting the minimum over [i, j]. Then the
range [i, j] can easily be presented as the union of the
following (at most) five ranges:
[i , x 1 ],[ x 1 + 1, x 2 ],[ x 2 + 1, x 3 ],[ x 3 + 1,x 4 ],[ x 4 + 1, j ]
i
j
Where:
[ i , x1 ] and [ x4+ 1, j ] fall within a single subset
partition of size loglogn, it’s minimum is available in it’s
subtable.
1.
[i , j ] =
[i , x 1 ],[ x 1 + 1, x 2 ],[ x 2 + 1, x 3 ],[ x 3 + 1,x 4 ],[ x 4 + 1, j ]
i
j
2.
[ x1+ 1, x2 ] and [ x3 + 1, x4 ] are unions of subset
partitions of size loglogn and fall within a single subset
of size logn it’s minimum is available from the
application of Procedure I on this subset.
[i , j ] =
[i , x 1 ],[ x 1 + 1, x 2 ],[ x 2 + 1, x 3 ],[ x 3 + 1,x 4 ],[ x 4 + 1, j ]
i
j
3.
[ x2 + 1 , x3 ] is the union of subsets of size logn each,
it’s minimum is available from the first application of
Procedure I.
[i , j ] =
[i , x 1 ],[ x 1 + 1, x 2 ],[ x 2 + 1, x 3 ],[ x 3 + 1,x 4 ],[ x 4 + 1, j ]
i
j
Space and Time Complexity
Did we archive linear space and time complexity, as
promised? let’s check.
Recall our preprocessing algorithm runs in three
stage. We’ll check each stage separately.
Denote n as the size of our input list L.
We assume n is a power of 2 for convenience
purposes.
The first stage space and time complexity can be
computed as follows:
Partitioning L into n/logn subsets of size logn each, and finding
each new subset’s minima:
Time: O( n ) - one pass through L is enough.
Space: O( n/logn ) – for storing all subset data.
Applying Procedure I on an array of n/logn minima:
Time and Space: according to Procedure I complexity:
O( n/logn log( n/logn )) O( n/ logn logn )
= O( n ).
n/logn < n
Total space and time complexity : O ( n ).
The second stage space and time complexity can
be computed as follows:
Partitioning each n/logn subset, into smaller subsets of size
loglogn each and finding each new subset’s minima:
Time: O( n ) - one pass through L is enough.
Space: O( n/loglogn ) – for storing all subset data.
Applying Procedure I on n/logn arrays of logn/loglogn minima:
Time and Space: according to Procedure I complexity:
n/logn O( logn/loglogn log( logn/loglogn ))
n/logn O( logn/ loglogn loglogn ) = O( n ). logn/loglogn < logn
Total space and time complexity : O ( n ).
The third stage simply runs Procedure II on inputs of
size loglogn. So the space and time complexity of the
third stage of the algorithm can be computed as
follows :
Time and Space: according to Procedure II complexity:
O ( 2loglogn log2logn ) = O( logn log2logn ) O ( log2n )
Total space and time complexity : O ( log2n ).
log2logn < logn
Aftermath
How much did we really gain by reducing the LCA
problem to the restricted range-minima problem?
Can we be satisfied by just reducing to the rangeminima problem?
If you recall, the restricted range-minima reduction
allows us to use Procedure II which assumes input of
restricted nature. We used Procedure II to answer
range queries of size on subsets of size equal or
smaller then loglogn.
We can instead apply Procedure I to each of these
loglogn subset which would total the space and time
complexity of the whole algorithm to O( nloglogn ).
If we choose to further partition these subset into
subsets of size logloglogn, we would reach
O(nlogloglogn). We can continue in this fashion for as
much as we like, improving our algorithm’s complexity
along the way.
If k is the number of partition stages our algorithm
applied, then it’s space and time complexity equals
O(nloglog … logn).
k
The space and Time complexity of our preprocessing
algorithm for the un-restricted range minima problem is
then : O(nlog*n) !
For practical applications the un-restricted range minima
reduction is enough then, considerably simplifying the
implementation process.
The restricted range minima reduction is needed mostly
for theoretical purposes.
Bibliography