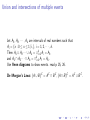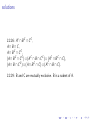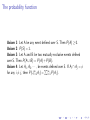* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download chapter2 part I
Survey
Document related concepts
Transcript
The evolution of the definition of probability
Classical probability: all outcomes are equally likely. well-suited
to gambling scenario.
If an experiment results in N equally likely outcomes and an event
A consists of n of these outcomes, then P(A) = Nn .
Empirical probability: long run frequency.
Axiomatic approach: Kolmogorov
Sample space and the algebra of sets
Sample space S : contains all possible outcomes of an experiment.
An event is a subset of the sample space.
e.g., flip a coin three times.
S = {HHH, HHT , HTH, THH, HTT , THT , TTH, TTT }.
A = {more heads than tails} = {HHH, HHT , HTH, THH}.
Infinite sample space: A coin is tossed until a tail appears.
S = {T , HT , HHT , HHHT , · · · }
Exercise: P 21: 2.2.10, 2.2.11.
How we formulate the sample space for a given situation will
depend on the problem at hand. It is desirable to use sample
spaces whose elements can not be divided into more elementary
kinds of outcomes.
Unions, intersections and complements
Let A, B be two events.
A ∩ B : intersection of A and B: the outcomes belong to both A
and B.
A ∪ B : union of A and B: the outcomes belong to either A or B or
both.
e.g. let A be the set of x 0 s for which x 2 + 2x = 8, B be the set for
which x 2 + x = 6.
Then A = {−4, 2}, B = {−3, 2}. Hence
A ∪ B = {−4, −3, 2}, A ∩ B = {2}.
A and B are said to me mutually exclusive if A ∩ B = φ, where φ
is the null set.
The complement of A, AC , consists of all outcomes in S other
than those in A.
Union and intersections of multiple events
Let A1 , A2 , · · · , Ak are intervals of real numbers such that
Ai = {x : 0 ≤ x ≤ 1/i, }, i = 1, 2, · · · , k.
Then A1 ∪ A2 · · · ∪ Ak = ∪ki=1 Ai = A1 ,
and A1 ∩ A2 · · · ∩ Ak = ∩ki=1 Ai = Ak .
Use Venn diagrams to show events. read p 25, 26.
De Morgan’s Laws: (A ∪ B)C = AC ∩ B C , (A ∩ B)C = AC ∪ B C .
Exercises, p 24
2.2.26: Let A, B, C be three events defined on S. Use unions,
intersections and complements to represent
1). none of the three events occurs.
2). all three of the events occur.
3). only A occurs.
4). exactly one event occurs.
5). exactly two events occur.
2.2.29: A coin is tossed 4 times.
Let A be exactly two heads appear, B be heads and tails alternate,
and C be first two tosses are heads.
1). Which events, if any, are mutually exclusive?
2). Which events, if any, are subsets of other sets?
solutions
2.2.26: Ac ∩ B C ∩ C C ,
A ∩ B ∩ C,
A ∩ BC ∩ C C ,
(A ∩ B C ∩ C C ) ∪ (AC ∩ B ∩ C C ) ∪ (AC ∩ B C ∩ C ),
(A ∩ B ∩ C C ) ∪ (A ∩ B C ∩ C ) ∪ (AC ∩ B ∩ C ).
2.2.29: B and C are mutually exclusive. B is a subset of A.
The probability function
Axiom
Axiom
Axiom
over S.
Axiom
for any
1: Let A be any event defined over S. Then P(A) ≥ 0.
2: P(S) = 1.
3: Let A and B be two mutually exclusive events defined
Then P(A ∪ B) = P(A) + P(B).
4: Let A1 , A2 , · · · , be events
P∞defined over S. If Ai ∩ Aj = φ
∞
i 6= j, then P(∪i=1 Ai ) = i=1 P(Ai ).
Some properties of probability
Theorems:
1. P(AC ) = 1 − P(A).
2. P(φ) = 0.
3. If A ⊂ B, then P(A) ≤ P(B).
4. For any event A, P(A) ≤ 1.
5. Let A1 , A, · · · , An be events
Pdefined over S. If Ai ∩ Aj = φ for
any i 6= j, then P(∪ni=1 Ai ) = ni=1 P(Ai ).
6. P(A ∪ B) = P(A) + P(B) − P(A ∩ B).
example 2.3.4
L: Lead actress appears in scene.
D: Double appears in scene.
It is given P(L) = 0.4, P(D) = 0.30, P(L ∩ D) = 0.05. Then
P(only double appears) =P(D) − P(L ∩ D) = 0.3 − 0.05 = 0.25,
P(neither appears) =1 − P(L ∪ D) =
1 − [P(L) + P(D) − P(L ∩ D)] = 1 − (0.4 + 0.3 − 0.05) = 0.35.
Exercises p 32
2.3.17: Let A, B, C be three evens defined over S. Arrange the
following probabilities from smallest to biggest.
A ∪ B, A ∩ B, A, S, (A ∩ B) ∪ (A ∩ C ).
2.3.18: Lucy is currently running two dot-com scams. She
estimated that the chances the first one leading to her arrest is
0.10, the second leading to her arrest is 1/30, and the likelihood
that she gets busted for both is 0.0025. What is her chance of
avoiding incarceration?
solutions
2.3.17: A ∩ B, (A ∩ B) ∪ (A ∩ C ), A, A ∪ B, S.
2.3.18: P(A) = 1/10, P(B) = 1/30, P(A ∩ B) = 0.0025.
1 − P(A ∪ B) = 1 − [1/10 + 1/30 − 0.0025] = 0.869.
Addition rule for three events: P(A ∪ B ∪ C ) =
P(A)+P(B)+P(C )−P(A∩B)−P(A∩C )−P(B ∩C )+P(A∩B ∩C ).
Conditional probability
Let A, B two events defined on S such that P(B) > 0. The
conditional probability of A given B is defined as
P(A|B) = P(A∩B)
P(B) .
The above definition gives the multiplication rule
P(A ∩ B) = P(A|B)P(B)
example 2.4.2: consider families having two children. Assume the 4
possible birth sequences (b, b), (b,g), (g, b) and (g, g) are equally
likely. What is the probability that both are boys given that at
least one is a boy? Let A: both are boys, B: at least one is a boy,
then
P(A|B) = P(A ∩ B)/P(B) = P(A)/P(B) = (1/4)/(3/4) = 1/3.
Use conditional probability to compute joint probability
There are 4 red balls and 3 black balls of the same size in a jar.
Randomly take out 1 ball, put it aside, then randomly take out
another ball.
(Note this is called sampling without replacement. Sampling
with replacement means you put the ball back each time.)
Find the probability that both balls are red.
P(1st Red and 2nd Red) = P(2nd Red|1st Red) ∗ P(1st Red) =
(3/6) ∗ (4/7) = 2/7.
The law of total probabilities
Theorem: Let Ai , i = 1, · · · , n be a set of events defined over S
such that S = ∪ni=1 Ai , Ai ∩ Aj = φ, for all i 6= j (this is called a
partition P
of S), and P(Ai ) > 0. For any event B,
P(B) = ni=1 P(B|Ai )P(Ai ). Proof see p. 43.
n
Note B =
P∪n i=1 (B ∩ Ai ) andPn
P(B) = i=1 P(B ∩ Ai ) = i=1 P(B|Ai )P(Ai ).
Example p. 45
.
Ashely is hoping to land a summer internship at a firm. She has a
chance of 0.7 of getting an offer if her interview goes well, but the
chance drops to 0.20 if the interview is a bust. Unfortunately for
Ashley that chance that the interview goes well for her is only
0.10. What is the probability that she will get an offer?
Let B: she gets an offer, A1 : the interview goes well, A2 : the
interview does not go well.
Then P(B|A1 ) = 0.7, P(B|A2 ) = 0.2, P(A1 ) = 0.10, P(A2 ) = 0.90.
P(B) = P(B|A1 )P(A1 ) + P(B|A2 )P(A2 ) = 0.7 ∗ 0.1 + 0.2 ∗ 0.9 =
0.25.
example
Suppose you will enter room A, B, C with probability 0.5, 0.25,
0.25 respectively. The probability that you will see a red light in
room A is 0.2, in room B is 0.5, in room C is 0.1. What is the
probability that you will see a red light?
P(red) = P(red|A)P(A) + P(red|B)P(B) + P(red|C )P(C ) =
0.2 ∗ 0.5 + 0.5 ∗ 0.25 + 0.1 ∗ 0.25 = 0.25.
Exercise
There are 4 red balls and 3 black balls of the same size in a jar.
Randomly take out 1 ball, put it aside, then randomly take out
another ball.
Find the probability that the second ball is red.
Compare it to the probability that the second ball is red under
sampling with replacement.