* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download ppt
Double-slit experiment wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Probability amplitude wikipedia , lookup
Canonical quantization wikipedia , lookup
Quantum teleportation wikipedia , lookup
Quantum dot cellular automaton wikipedia , lookup
Coherent states wikipedia , lookup
Quantum decoherence wikipedia , lookup
Bell test experiments wikipedia , lookup
Quantum state wikipedia , lookup
Quantum group wikipedia , lookup
Measurement in quantum mechanics wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Bell's theorem wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Boson sampling wikipedia , lookup
Quantum entanglement wikipedia , lookup
Wheeler's delayed choice experiment wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Density matrix wikipedia , lookup
Quantum key distribution wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
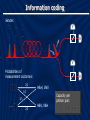
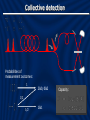
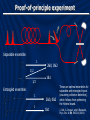
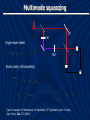
Squeezing eigenmodes Entanglement-enhanced in parametric downcommunication over conversion a correlated-noise channel Konrad Banaszek Nicolaus Copernicus University Toruń, Poland Andrzej Dragan Wojciech Wasilewski Czesław Radzewicz Warsaw University Jonathan Ball Alex Lvovsky University Oxford University ofofCalgary National Laboratory for Atomic, Molecular, and Optical Physics, Toruń, Poland Mutual information: Channel capacity: Receiver Sender All that jazz Depolarization in an optical fibre Photon in a polarization state Independently of the averaged output state has the form: Random polarization transformation V H 1/2 1 1/2 H 1/2 2 1/2 V Capacity of coding in the polarization state of a single photon: Information coding Sender: V H V Probabilities of measurement outcomes: 2/3 1/3 H H&H, V&V 1/3 2/3 H&V, V&H Capacity per photon pair: Collective detection Probabilities of measurement outcomes: 1 2&0, 0&2 1/2 1/2 1&1 Capacity: Entangled states are useful! Probabilities of measurement outcomes: 1 1 2&0, 0&2 1&1 Capacity: Proof-of-principle experiment Separable ensemble: 1 1/2 1/2 2&0, 0&2 1&1 Entangled ensemble: 1 1 2&0, 0&2 1&1 These are optimal ensembles for separable and entangled inputs (assuming collective detection), which follows from optimizing the Holevo bound. J. Ball, A. Dragan, and K.Banaszek, Phys. Rev. A 69, 042324 (2004) Source of polarization-entangled pairs P. G. Kwiat, E. Waks, A. G. White, I. Appelbaum, and P. H. Eberhard, Phys. Rev. A 60, R773 (1999) For a suitable polarization of the pump pulses, the generated two-photon state has the form: With a half-wave plate in one arm it can be transformed into: or Experimental setup K. Banaszek, A. Dragan, W. Wasilewski, and C. Radzewicz, Phys. Rev. Lett. 92, 257901 (2004) Triplet events: D1 & D2 D3 & D4 Singlet events: D1 & D3 D2 & D3 D2 & D3 D2 & D4 Experimental results Dealing with collective depolarization 1) Phase encoding in time bins: fixed input polarization, polarization-independent receiver. J. Brendel, N. Gisin, W. Tittel, and H. Zbinden, Phys. Rev. Lett. 82, 2594 (1999). 2) Decoherence-free subspaces for a train of single photons. J.-C. Boileau, D. Gottesman, R. Laamme, D. Poulin, and R. W. Spekkens, Phys. Rev. Lett. 92, 017901 (2004). General scenario Physical system: • arbitrarily many photons • N time bins that encompass two orthogonal polarizations • How many distinguishable states can we send via the channel? • What is the biggest decoherence-free subspace? Mathematical model General transformation: where: – the entire quantum state of light across N time bins – element of U(2) describing the transformation of the polarization modes in a single time bin. – unitary representation of W in a single time bin We will decompose and with Schwinger representation Ordering Fock states in a single time bin according to the combined number of photons l: ... Representation of W: ... Here Consequently is (2j+1)-dimensional representation of SU(2). has the explicit decomposition in the form: Decomposition Decomposition into irreducible representations: Integration over a removes coherence between subspaces with different total photon number L. Also, no coherence is left between subspaces with different j. tells us: • how many orthogonal states can be sent in the subspace j • dimensionality of the decoherence-free subsystem Recursion formula for : J. L. Ball and K. Banaszek, quant-ph/0410077; Open Syst. Inf. Dyn. 12, 121 (2005) Biggest decoherence-free subsystems have usually hybrid character! Questions • Relationship to quantum reference frames for spin systems [S. D. Bartlett, T. Rudolph, and R. W. Spekkens, Phys. Rev. Lett. 91, 027901 (2003)] • Partial correlations? • Linear optical implementations? • How much entanglement is needed for implementing decoherence-free subsystems? • Shared phase reference? • Self-referencing schemes? [Z. D. Walton, A. F. Abouraddy, A. V. Sergienko, B. E. A. Saleh, and M. C. Teich, Phys. Rev. Lett. 91, 087901 (2003)] • Other decoherence mechanisms, e.g. polarization mode dispersion? Multimode squeezing SHG Single-mode model: PDC Brutal reality (still simplified): [See for example: M. Matuszewski, W. Wasilewski, M. Trippenbach, and Y. B. Band, Opt. Comm. 221, 337 (2003)] – Perturbative regime The wave function up to the two-photon term: W. P. Grice and I. A. Walmsley, Phys. Rev. A 56, 1627 (1997); T. E. Keller and M. H. Rubin, Phys. Rev A 56, 1534 (1997) Schmidt decomposition for a symmetric two-photon wave function: C. K. Law, I. A. Walmsley, and J. H. Eberly, Phys. Rev. Lett. 84, 5304 (2000) We can now define eigenmodes The spectral amplitudes which yields: characterize pure squeezing modes Decomposition for arbitrary pump As the commutation relations for the output field operators must be preserved, the two integral kernels can be decomposed using the Bloch-Messiah theorem: S. L. Braunstein, quant-ph/9904002; see also R. S. Bennink and R. W. Boyd, Phys. Rev. A 66, 053815 (2002) Squeezing modes The Bloch-Messiah theorem allows us to introduce eigenmodes for input and output fields: which evolve according to • • describe modes that are described by pure squeezed states tell us what modes need to be seeded to retain purity Some properties: • For low pump powers, usually a large number of modes becomes squeezed with similar squeezing parameters • Any superposition of these modes (with right phases!) will exhibit squeezing • The shape of the modes changes with the increasing pump intensity! This and much more in a poster by Wojtek Wasilewski The End Theory Everything that emerges are Werner states One-dimensional optimization problem for the Holevo bound What about phase encoding? Recursion formula Decompostion of the corresponding su(2) algebra: If we subtract one time bin: Direct sum The product of two angular momentum algebras has the standard decomposition as: Therefore the algebra for L photons in N time bins can be written as a triple direct sum: Decoherence-free subsystems Rearranging the summation order finally yields: Underlined entries with correspond to pure phase encoding (with all the input pulses having identical polarizations) – in most cases we can do better than that!