Download ME 230 - Dynamics

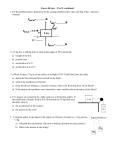
ME 230 - Dynamics
Tutorial 3
Partners:_________________
_________________
Your Name:_________________
Section No.:_________________
_________________
_________________
_________________
_________________
Newton’s 2nd Law
This tutorial will examine methods of using Newton’s Second Law in solving kinetics
and kinematics problems. A physical model of the first problem will be used to lend realworld significance and to confirm the analytical results.
1)
A block resting on a ramp is attached to a string that is pulled up a ramp by a
force gauge. We wish to develop a procedure to determine the static and kinetic
coefficients of friction. Following that we will use Newton's Second Law and
determine the motion of the block when pulled up the ramp by a weight.
i)
Draw a FBD of the block on a ramp inclined at an angle .
ii)
Perform a static analysis to symbolically determine the static coefficient of
friction between the block and the ramp from the weight of the block W and the
tension T applied by the force gauge and the angle .
iii)
Measure the weight of the block and the angle of the ramp and perform a series of
experiments to determine the minimum tension necessary to move the block.
Compute the static coefficient of friction from your results.
Wblock _________ lb
Ramp angle  = _________ degrees
iv) As a check on your result for the static coefficient of friction, compute the minimum
tension to move the block on a level surface, measure that tension in a series of
experiments, and compute the static coefficient of friction and compare the result with
that obtained from ramp angle .
iv)
We now wish to analyze the motion of the block in a dynamic configuration to
determine the kinetic coefficient of friction. Repeat the previous series of
experiments while pulling the block at a constant speed with a constant tension as
determined by the force gauge. (Note the kinetic coefficient of friction must be
smaller than the static one.)
v)
We now wish to analyze the motion of the block if it were pulled up a ramp by a
weight force. Draw three separate FBDs of the block on the ramp, the pulley, and
the weight.
vi.
Using Newton’s Second Law, determine the acceleration of the block up the ramp
if the weight force were 2 lb. Think ..Is the acceleration constant?

a =_______ft/sec2
2)



The acceleration of the 20-lb collar A is 2i  3 j  3k ft/sec2. What is the

magnitude of the force F ? (Text problem 3.53)
i.
Draw a FBD of the collar, showing the vector forces acting on it.
ii.
Symbolically describe the solution to this problem by using Newton’s Second


Law,  F  ma . (That is, write the relevant forces, mass, and acceleration in symbolic
vector form.) Hint: dot products and unit vectors may be useful here, because you need to
resolve the forces and acceleration in a direction parallel to the bar.
iii.

Solve for the magnitude of F .
3)
A 4 lb ball revolves in a horizontal circle as shown. Knowing that L=3 ft. and that
the maximum allowable tension in the cord is 10 lb, find a) the maximum allowable
speed, and b) the corresponding angle of  . (Hint: solve using normal and tangential
components.)
i.
Draw a FBD of the ball. It is suggested that you show a “side” view, with the
origin of a Cartesian reference frame at the center of the ball.
ii.
Ask yourself: What is the tangential acceleration in this case? Why?
v2
iii.
Is there a normal acceleration component? Normal acceleration an  . Write
p
an expression for a n .
iv.
Using Newton’s Second Law, solve for the maximum allowable speed, v, and for
the corresponding angle,  .