* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Resources for students entering Algebra II w/ Trigonometry
Bra–ket notation wikipedia , lookup
Line (geometry) wikipedia , lookup
History of trigonometry wikipedia , lookup
History of mathematical notation wikipedia , lookup
List of important publications in mathematics wikipedia , lookup
Recurrence relation wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Elementary algebra wikipedia , lookup
System of polynomial equations wikipedia , lookup
Partial differential equation wikipedia , lookup
Signal-flow graph wikipedia , lookup
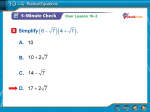
NAME: _____________________________ ALGEBRA II W/ TRIGONOMETRY OPTIONAL SUMMER WORK I. Evaluating Algebraic Expressions & Functions To evaluate an algebraic expression: Substitute the given value(s) of the variable(s). Use order of operations to find the value of the resulting numerical expression. Evaluate. 1) b b 2 4ac if a 1, b 4, c 21 2a 2) A P 1 nt r n if P = 650, r = 6%, n = 2, t = 15 Evaluate the following functions given: x f(x) = 4x – 12x + 7x 2 3) f(–3) 3 4) æ1ö g(x ) = 2 çç ÷÷ è 3ø h(x ) = g(2) 5) 4-x -x 2 h(f(1)) II. Simplifying Radicals An expression under a radical sign is in simplest radical form when: 1) there is no integer under the radical sign with a perfect square factor, 2) there are no fractions under the radical sign, 3) there are no radicals in the denominator Express the following in simplest radical form. 1) æ è öæ øè ö ø 2) ç3 + 2 3 ÷ ç2 - 5 3 ÷ 50 3) 3 2 + 4 8 - 5 50 4) 6 27 III. Properties of Exponents PROPERTY Product of Powers a a =a x x =x Power of a Power (am)n = am n (x4)2 = x8 Power of a Product (ab)m = ambm (2x)3 = 8x3 Negative Power EXAMPLE m n m+n 1 an a-n = Zero Power a0 = 1 Quotient of Powers am = am – n n a Power of Quotient am a = bm b 4 2 1 x3 (a 0) x-3 = (a 0) 40 = 1 (a 0) x8 x6 2 x 3 m (b 0) x x3 y3 y 6 Simplify each expression using the exponent rules. Answers should be written using positive exponents. 1) g5 · g11 __________ 2) (b6)3 __________ 3) w-7 __________ 4) y 12 y8 __________ 5) (3x7)(-5x3) __________ 6) (-4a5b0c)2 7) - 15x 7 25x 9 __________ 8) æ 4x 9 çç 4 è 12x 9) ( 28m 3n -2 -2 4m -11n 4 ) __________ 10) ö ÷÷ ø __________ 3 __________ (3d m ) (2d m) (4d m ) 4 2 2 -2 -7 __________ 7 IV. Solving Equations Solve for the indicated variable. Express all answers as fractions in lowest terms. Circle your answers. 1) 2[x + 3(x – 1)] = 18 3) 2x2 = 50 2) 6 + 2x(x – 3) = 2x2 4) x + 4 + 8 = 2x + 4 5) 2 3 x - 18 = x 6) 6 x -2 3 = 2x + 1 4 V. Operations With Polynomials Perform the indicated operations and simplify (meaning collect similar terms). 1) (5x2 - 4) – 2(3x2 + 8x + 4) 2) 3) (5x – 6)2 (7x - 3)(3x + 7) VI. Inequalities Solve and graph the following inequalities on a number line. Write your final answer in interval notation. 1) 4(x + 5) > 2x - 8 2) 2x - 3 > 9 or 3x £ 12 3) -3 £ 2x - 11 < 7 VII. Factoring Polynomials Factor the following completely. 1) 16y2 + 8y 2) x2 + 11x + 24 3) 3m2 - 3m + 10mn – 10n 4) x2 - 2x – 63 5) 6y2 - 13y – 5 6) 4x2 - 121 VIII. Linear Equations in Two Variables 1) Write an equation, in slope-intercept form using the given information. a. (5, 4) m = - 2 3 b. (-2, 4) m = -3 c. (-6, -3) (-2, -5) 2) In 1998, Margo had $429 in her bank account. By 2010, she had $2540. Find the rate of change for her bank account. 3) Kim and Cyndi are starting a business tutoring students in math. They rent an office for $400 per month and charge $40 per hour per student. a) Write a linear equation to represent this situation. b) If they have 15 students each for one hour per week how much income do they make together in a month? (assume 4 weeks per month) c) If they earn a total of $3760 in February, how many tutoring sessions did they provide that month? IX. Graphing Linear Equations Graph each of the following linear equations. y= 1) 2 3 x -4 2) x + 3y = 6 3) y+2=7 X. Solving Systems of Equations Solve each system of equations algebraically. 1) y = 2x + 4 -3x + y = - 9 2) 2x + 3y = 6 -3x + 2y = 17 XI – Right Triangles Find the missing side length(s): Pythagorean Theorem: 1) 2) 41 3 5 3 2 9 Special Right Triangles (30-60-90) Special Right Triangles (45-45-90) Trigonometry (SOHCAHTOA) XII. – Scatter Plots Below is a chart showing number of calories in food served at Wendy’s as well as the calories of fat in the specific food. Draw a scatter plot (use an appropriate scale!!) for the information and then answer the questions below. (3 pts) # calories (x-axis) # g of fat (y-axis) 530 28 500 24 180 12 450 30 580 31 670 32 500 33 310 16 1090 290 66 13 1. What type of correlation is there on the scatter plot you drew below? 2. Draw a line of best of fit for the graph and find the equation for the line of best fit. Round all numbers to the nearest thousandth 3. How many calories would you expect something to have if it had 44 g of fat? 4. How many grams of fat would you expect something with 800 calories to have?