* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Rate Of Change Assignment
Survey
Document related concepts
Transcript
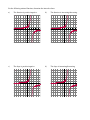
Rational Functions and Rate of Change For the function: y = 6 x2 y a) On the graph, draw a tangent line at x = -1. b) Using the graph, determine the slope of the tangent (instantaneous rate of change) at x = -1. c) Using the graph, determine the equation of the tangent line (y = mx + b). d) Using the equation, determine the slope of the tangent (instantaneous rate of change) at x = -1. e) How does the slope from d) compare to the slope from b)? Which do you think is more correct? Explain. Identifying Characteristics of Functions For the following polynomial function, determine the intervals where: a) The function is positive/negative. b) y The function is increasing/decreasing. y x c) The slope is positive/negative. d) y The slope is increasing/decreasing. y x For the following rational function, determine the intervals where: a) The function is positive/negative. b) y The function is increasing/decreasing. y x c) The slope is positive/negative. d) y The slope is increasing/decreasing. y x Rational Functions & Rate of Change Practice 1. For each of the following functions, state the intervals where: The function is positive/negative The function is increasing/decreasing The slope of the tangent is increasing/decreasing a) y b) y x x 2. For each of the following functions, sketch the function and then state the intervals where: The function is positive/negative The function is increasing/decreasing The slope of the tangent is increasing/decreasing 1 2 5 a) y = b) y = c) y = x6 2x 1 1 x 10 : 3x 2 a) Determine the average rate of change between x = 1 and x = 6. b) Determine the instantaneous rate of change at x = 1. 3. For the function f(x) = 4. Determine the equation of the tangent line to the function y= 8 at the point x = 1. 5x 3 280 , where D 10 D is the diver’s depth below the surface in metres. Determine the rate at which the volume of air in the scuba diver’s lungs is changing, when the diver is 10 m below the surface. 5. The volume of air in a scuba diver’s lungs (V) varies according to the equation V =