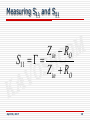* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download RF Microelectronic
Standing wave ratio wikipedia , lookup
Audio crossover wikipedia , lookup
Immunity-aware programming wikipedia , lookup
Integrating ADC wikipedia , lookup
Superheterodyne receiver wikipedia , lookup
Telecommunication wikipedia , lookup
Spectrum analyzer wikipedia , lookup
Power electronics wikipedia , lookup
Schmitt trigger wikipedia , lookup
Transistor–transistor logic wikipedia , lookup
Analog-to-digital converter wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Operational amplifier wikipedia , lookup
Regenerative circuit wikipedia , lookup
Radio transmitter design wikipedia , lookup
Mixing console wikipedia , lookup
Opto-isolator wikipedia , lookup
Rectiverter wikipedia , lookup
Phase-locked loop wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
RF Microelectronic LNA and Mixer Oscillator KAVOSHCOM Contents 1. 2. 3. 4. 5. 6. 7. 8. 9. Introduction Basic concepts Digital modulation, Spectral control, Detection Multiple access standards, TDM, CDM, OFDM TRx architecture LNA and Mixer Oscillator Frequency Synthesizer Power Amplifier April 30, 2017 2 Section 6 6. LNA and Mixers a) LNA i. Input matching vs. NF ii. BJT vs. CMOS iii. BW enhancement b) Mixer i. BJT Mixers ii. CMOS Mixers iii. Noise in Mixers c) Cascaded stages April 30, 2017 3 LNA Figures of Merit Frequency Noise Figure Linearity (P-1dB, IIP3) Bandwidth and Q Gain S21 Power Consumption Supply Voltage S-Parameters Gain S21 Input Matching S11 Output Matching S22 Reverse Isolation S12 Stability Image Rejection Capability April 30, 2017 4 Typical Figures of Merit NF ~ 2dB IIP3 ~ -10 dBm P-1dB ~ -20 dBm Gain ~ 15 dB Input and Output Return Loss: S11, S22 Reverse Isolation:S12 Zin=Zout < -15 dB April 30, 2017 < - 30 dB =50Ω 5 LNA Design Input Matching Network Noise and Linearity Consideration Output Loading and Gain Output Matching Network Stability Differential Design April 30, 2017 6 Noise Figure of LNA LNA, the first gain stage in the receive path Noise figure directly adds to that of the system its Duplexer Noise Figure ~ 2dB System Noise Figure=4dB LNA noise Figure =2dB SNRmin S N 8dB in NBW 200 KHz April 30, 2017 S N out NF S min 109dBm 8dB 7 Noise Figure of LNA LNA=2dB using BJT: =2KTgm (shot noise) 4KTrb Vneq 2 Vneq April 30, 2017 2 2 KTg m 4 KTrb 2 gm & Ic gm VT Vneq 2 Req VT 4 KT (rb ) NF 1 1 2I c 4 KTRs Rs 8 Noise Figure of LNA VT Req rb 2I c For NF=2dB Req < 29Ω Q1 must be relatively large and biased at a high current Finger structure reduces rb but increases capacitance Bandwidth reduction April 30, 2017 9 Minimum Gain of LNA Defined by Three parameters: Loss of the image-reject filter Noise Figure of mixer IP3 of the Mixer For example: Filter loss=4~5 dB Mixer noise figure=10dB Gain=20dB Mixer IP3=+5dBm min. Input-referred noise is suppressed reasonable equivalent IP3 is maintained April 30, 2017 10 Input and Output Matching Input Impedance is 50Ω because it comes out of the antenna Output Impedance can be>=50Ω whether it goes to IC The quality of the input matching is expressed by: Input Return Loss=20log|Γ| Γ=the reflection coefficient with respect to a source impedance R0 For Impedance Matching: Γ<0.2 April 30, 2017 11 Measuring S11 and S21 April 30, 2017 12 Measuring S11 and S21 Z in RO S11 Z in RO April 30, 2017 13 Input and Output Matching Γ=0.2 Zin=35Ω_65Ω |S11|35=((35-50)/(35+50))^2|dB=-15dB |S11|65=((65-50)/(65+50))^2|dB=-17.6dB In RF Circuits : Impedance matching Max Power Transfer In LNA Design: R sopt We accept mismatch in the first stage But we try to select the device in a way to have Matching circuit 50Ω 50Ω April 30, 2017 Rsopt~50Ω Rsopt 50Ω 50Ω 50Ω 50Ω 50Ω 14 Input and Output Matching In IC design when the receiver sensitivity is very important e.g. GPS, external discrete LNA placed on the PCB is desirable In mass productive ICs e.g. for Mobile handsets, we try to design input LNA, Zin=Rsopt~50Ω LNA output Impedance must also equal 50Ω to have the minimum loss and ripple in driving Image-Reject Filter April 30, 2017 15 LNA stability Due to feedback from the output to input, the circuit may become unstable for certain amounts of source and load Impedance The amount of feed-back can also set the reverse isolation of the amplifier which is important for LO radiation. April 30, 2017 16 LNA stability Stern Stability Factor : 1 S11 S 22 K 2 S 21 S12 2 2 2 S11S 22 S12 S 21 If K>1 & Δ<1 The circuit is unconditionally stable Difficulty: S parameters must be calculated for a wide frequency range to ensure that K>1 at all frequencies April 30, 2017 17 LNA stability If S12 0 then: K Δ ∞ S11.S22<1 (both S11 & S22 inside the unit circle of the smith chart) This function is called “Neutralization” of the return path April 30, 2017 18 Stabilization by Neutralization L1 and C1 actually tune out the parasitic capacitance At a frequency thus S12=0 April 30, 2017 19 Stabilization by Cascoding In IC design the feedback can be suppressed by cascode configuration Variation of the node X is small due to Vb so the effect on Vin is low enough to reduce S12 April 30, 2017 X 20 Is the LNA stable anyway? Vcc and GND leakage paths and substrate of ICs still have to be considered Isolating Vcc and GND is a solution Differential structure is useful for c.m. signal rejection Problem: Differential LNA design is not easy because of matching constraints April 30, 2017 21 Is the LNA stable anyway? April 30, 2017 22 PCB Ground Consideration April 30, 2017 23 Impedance matching in MOS LNA A common-source stage in order to create 50Ω input Impedance April 30, 2017 24 Impedance matching in MOS LNA Yin Yinr jYini Yinr RL C F 2 C F g m RL (C L C F ) 2 RL (C L C F ) 2 2 1 RL C L (C L C F ) 2 1 g m RL Yini C F 2 RL (C L C F ) 2 2 1 2 if C L C F & g m RL 1 1 RL C L g m CF Yinr . 2 CL g m RL Yini C F (1 ) 2 Proper selection of 2CL/gmCF makes 50Ω input resistance but the drawback is the relatively low voltage gain at high frequencies due To bandwidth limitation at the output node April 30, 2017 25 Resistive Termination In high frequencies, Capacitive part of the input impedance must be cancelled by an external inductor Noise figure is at least 3dB (NF=1+Rs/RP , Rs = RP) April 30, 2017 26 Input Resistive Termination by Negative Shunt Feedback Low input impedance with a 50Ω real part can be obtained April 30, 2017 27 Input Resistive Termination by Negative Shunt Feedback Drawbacks: Active feedback injects noise in the input of the circuit Frequency stability can be ruined because of the creation of a loop April 30, 2017 Either compensation (BW reduction) or oscillation risks should be accepted 28 Common-gate stage design Trade-off between noise figure and input matching April 30, 2017 29 Common-gate stage design Input resistance of 50Ω is achieved by proper Bias parameters 1 Rin g m g mb The drawback is worse Noise Figure: 4 KTg m 4 KTRs 2 gm gm NF 1 4 KTRs Rs if : April 30, 2017 Rs ~ 1 gm NF 1 30 Common-gate stage design Long channel devices (1-10μm) γ=0.66 Short channel devices(0.18-0.5μm) γ=3~4 High noise Figure in recent technology April 30, 2017 31 Resistive termination by Inductive Degeneration LS X Vref For Bias April 30, 2017 32 Resistive termination by Inductive Degeneration Freedom in tuning Zin is obtained g m L1 1 Z in L1 S LS S CGS CGS S L1 is tuned to have 50Ω by the first statement LS is added to reject the second and third statement Vref is placed for Bias The circuit is designed in an iterative process L1 degenerates the gain April 30, 2017 33 Bipolar LNA with Replica Biasing I1 is passed through Q1 so thermal matching is obtained April 30, 2017 34 Bipolar LNA R1 & R2: Compensate the effect of β (Base Current) Reducing the value of C1 that rejects the Biasing circuit’s Noise (Since the input Impedance is increased, smaller capacitor can be used) R2 causes approximately equal VBE for transistors so thermal matching is obtained Noise of R1 can not be rejected because the signal will be grounded if the capacitor is placed before R1 April 30, 2017 35 Bipolar LNA Noise Figure is considered as the following: Shot noise of Collector 4KT/2gm Rb g m RS 1 NF 1 RS 2 g m RS 2 1 2 g m Rb Rb g m RS 1 NFmin RSOPT RS 2 g m RS 2 gm NFmin 1 April 30, 2017 Shot noise of Base 4KTgm/2β 1 2 g R m b 36 IP3 calculation IC I S VBE Vin exp VT 2 3 VBE Vin 1 Vin 1 Vin 1 I S exp ... VT VT 2 VT 6 VT 4 1 iip 3 2 2VT 3 3 voltage April 30, 2017 if Rin 50 then iip 3 12.3dBm Power 37 Comparison With MOS, better values of iip3 is considerable MOS does not have shot noise so we do not have an optimum value for noise In order to have controlled NF, discrete circuit has to be implemented because inside the IC, β and Rb are not controllable April 30, 2017 38 Some State-Of-The-Art LNAs MEYER & MACK Common-Base LNA CMOS LNA: Karanicolas IEEE Journal of Solid-State Circuits, Vol.29, PP.350-355, March 1994 IEEE Journal of Solid-State Circuits, Vol.31, PP.1939-1944, December 1996 LNA implemented with MESFETs April 30, 2017 39 A 900MHz Bipolar LNA MEYER & MACK Defines DC level of the output Negative feedback April 30, 2017 Opens the feedback at high frequencies 40 A 900MHz Bipolar LNA First Stage: Second Stage: provides much of the gain controls Noise Figure Lower Gain Controls Zout Rf & RE effectively linearize the second stage Le improves ip3 because of its re like effect re is proportional to VT, ip3 (voltage)=2√2VT April 30, 2017 41 A 900MHz Bipolar LNA Thermal stability of the gain is considered as follows: Vb1 R1I c VBE 3 VBE 2 Vb1 VBE 3 VBE 4 0 I C1 RC1 Vb1 VPTAT 2VBE VPTAT I C1 RC1 I C1 VPTAT Gain of the first stage g m1.RC1 RC1 cte VT VT April 30, 2017 42 A 900MHz Bipolar LNA Le also provides conjugate matching of the input g m Le 1 Z in rb Le S C C S With proper choice of gm, Le, CΠ: g m Le Z in rb 50 C The last two terms cancel April 30, 2017 43 Common-Base LNA The source resistance Rs linearizes the input-output characteristic Rin April 30, 2017 44 Common-Base LNA Rin is used to reduce current but it worsens the NF Although BJT, but the circuit is very linear 1/gm<<Rs so in the voltage divider, the lower voltage causes little variation and consequently better linearity April 30, 2017 45 Common-Base LNA With Rin=0 Rs=1/gm=50Ω iip3≈-6.8dBm High reverse isolation is achieved if the base bias is properly bypassed Relatively high noise figure is the drawback April 30, 2017 46 MOS LNA Karanicolas M3 For Bias April 30, 2017 47 MOS LNA Vref and W/L of M3 changes the Bias current The capacitor makes the gain for M1 otherwise bypasses the feedback in AC The bias current is reused to provide a higher equivalent transconductance: (gm1+gm2) 1 Gain g m1 g m 2 g ds1 1 g m1 g m 2 g ds 2 g ds1 g ds 2 The circuit is followed by a similar stage so as to drive a 50-Ω load April 30, 2017 48 MOS LNA 900-MHz LNA & 2.7-V Vcc in CMOS 0.5μm technology NFmin=1.9 dB External matching network Gain=15.6 dB iip3=-3.2 dBm 20mW power consumption 7mA April 30, 2017 49 LNA implemented with MESFETs Recently implemented with CMOS April 30, 2017 50 LNA implemented with MESFETs Both M1 and M2 use the same Bias current Power is saved Drawback The parasitic bottom plate of C1 limits the RF gain at node X or Y April 30, 2017 51 BW enhancement 1.5GHz CMOS LNA April 30, 2017 52 BW enhancement On-chip and off-chip inductors are employed Ls and L1 create conjugate matching at the input At 1.5GHz, high gain is provided by the on-chip inductor LD Roles of using M2 by increasing the reverse isolation: Reduces LO leakage of the following mixer This Cascode device minimizes the feedback from output to input Inductive peaking is caused by LD It can cause near 500MHz increase in BW April 30, 2017 53 Mixer, general considerations Multiplier (Weak LO) Mixer (Large LO) instrumentation Passive April 30, 2017 Active 54 active mixer The circuit does not provide Gain Otherwise passive Active Sample of an active mixer on the next slide The drain current of M1 multiplied by a square wave routed to R1 and R2 alternately LO signal is powerful thus either M2 or M3 is off Cascode amplifier is obtained April 30, 2017 55 Active mixer April 30, 2017 56 Active Mixer Gain g m1 .R1 Fourier expansion of the pulse 4 1 VIF VRF .g m1 .R1 . 2 Multiplication of two sine waves VRF VIF 50Ω e.g. 1500Ω VLO April 30, 2017 57 Active Mixer G power April 30, 2017 VIF 2 1500 VIF 50 2 20 log 10 log VRF 1500 VRF 50 dB GVoltage 58 SSB and DSB Noise Figure SSB: the desired signal spectrum resides on only one side of the spectrum (a common case in heterodyne receivers) DSB: the desired signal spectrum resides on both sides of the spectrum (a common case in ZeroIF receivers) April 30, 2017 59 SSB NF Upon downconversion, 1. 2. 3. the signal the noise in the signal band the noise in the RF band Translated to ωIF IF noise April 30, 2017 60 SSB NF If: The input frequency response of the mixer is the same for: 1. 2. The signal band The image band Then: Output SNR=½ Input SNR NFnoiseless mixer=3dB April 30, 2017 61 DSB NF The input and Output SNRs are equal NFnoiseless mixer=0 dB April 30, 2017 62 SSB NF vs. DSB NF SSBNF DSBNF 3dB RF noise components around 3ωRF, 5ωRF, …are downconverted to the IF further increasing the output noise power Often negligible here but not in phase noise calculation April 30, 2017 63 Single Balanced Mixers Single Balanced: differential LO but a single-ended RF April 30, 2017 64 Double Balanced Mixers Both LO and RF signals are differential April 30, 2017 65 SB vs. DB Mixers In SB, M2 & M3 operate as a differential pair so LO amplified. If I F not much lower than LO, the LPF following the mixer may attenuate IF signal in order to suppress LO feedthrough thus the large LO content desensitizes the IF signal In DB, M3-M4 and M5-M6, add the amplified IF with opposite phases providing the first-order cancellation April 30, 2017 66 Comparison Single ended operation at the output ruins the advantages of double balanced configuration Low-frequency components in RF signal appear at the output without attenuation called direct feedthrough It also increases the noise figure of the mixer Despite the advantages of differential output, singleended output is required because of IF SAW filter present as the next stage External LC network makes the conversion April 30, 2017 67 Conversion of differential to single-ended output To reduce the effect of direct feedthrough and achieve the maximum gain April 30, 2017 68 Mixer Spurious Response Mixer as a nonlinear device, generates various crossproducts of the RF and LO signals |mωRF ± nωLO | Except for |ωLO-ωRF|, such components do not fall in the IF band Spurious response for different combination of m and n must be analyzed in the design April 30, 2017 69 BJT Mixers_a RF applied to Base April 30, 2017 70 BJT Mixers_b RF applied to Emitter I April 30, 2017 71 Comparison The nonlinearity in both of them is because of re Vt re I VRE IRE to reduce nonlinearity : RE re VRE 4Vt April 30, 2017 RE 72 Comparison Linearity of circuit b is better than a because in a, there would be a large voltage drop due to increase of RE. The presence of the capacitor in circuit b avoids DC so larger values of RE is possible I VRF 1 RS RE gm increasing RE causes: Lower Gain More input noise April 30, 2017 73 Comparison RE reduces the effect of nonlinearity caused by 1/gm but there are some other reasons for nonlinearity: Two extremely nonlinear capacitors exist Cb proportional to I April 30, 2017 Cb proportional to I 74 Comparison The equivalent capacitor of the upper tree (switches), halt proper operation of the ideal switch There some methods of reducing these capacitors with their own drawbacks Reducing transistor sizes (upper tree) but larger rb increases noise Shortening the transition time by larger LO amplitude but reducing switching time Designing a circuit to sense the voltage at point P and providing the required current for the capacitors at the moment Deleting the current of the bottom transistor at the switching time of the upper transistors April 30, 2017 75 Comparison Reverse Isolation of circuit b is better: Zin of circuit b is controlled by RE but in a by βRE Leakage of LO at point P transfers to the input through Ccb in circuit a but in b, there exists no collector-emitter capacitor so leakage is smaller β is frequency dependent Why is Zin important? The behavior of external filters like SAW or Crystal ones is defined by source impedance ZS and Load impedance Zin. If frequency dependent, there would be ripples in passband and the attenuation frequencies vary April 30, 2017 76 One Method of Linearization Gilbert Cell, extensively used, allows linearization of RF port Different Emitter areas are used in differential pairs Two such pairs are cross-connected Transconductance Gm grows as a function of the input voltage April 30, 2017 77 One Method of Linearization Gm vs. Vin April 30, 2017 78 CMOS Mixers Active Mixer April 30, 2017 79 CMOS Mixer The upper tree requires greater voltage swings to be able to switch( at least VTH ) than its Bipolar counterparts For lowering the swing for upper tree switching: Increasing the ratio W/L Lowering the upper tree’s current thus the current of M1 is decreased gm of M1 decreases thus total gain is reduced For the purpose of linearizing M1: (VGS-VT) transconductance noise figure conversion gain The trade-off between Gain and Linearity is problematic April 30, 2017 80 Passive CMOS Mixer M1 and M2 are driven by complementary phases of LO April 30, 2017 81 Passive CMOS Mixer Advantages: Higher ip3 if a large gate-source overdrive voltage (VGS-VT) is used for M1 and M2 in the on state so that VRF does not vary their on-resistance No power is drawn from the supply voltage Drawbacks: Because of the gain below unity, the noise figure of the following stages is magnified The large width requirement of M1 and M2 for low on-resistance leads to capacitive feedthrough from LO to IF The linearity advantage diminishes at low supply voltages (sub micron new devices) because of being near subthreshold region, Ron is severely nonlinear and VRF varies the switch onresistance, thus introducing distortion April 30, 2017 82 Noise in Mixers Sources of noise in a single-balanced mixer: April 30, 2017 83 Noise in Mixers 1. 2. 3. 4. 5. 6. Thermal noise due to the base resistance of Q1 Collector shot noise of Q1 Thermal noise due to the emitter resistor RE Collector shot noise of Q2 and Q3 Thermal noise due to the base resistance of Q2 and Q3 In the IF path, resistors RC1 and RC2 introduce thermal noise April 30, 2017 84 Noise in Mixers Noise 1, 2, 3, translated from RF to IF Images of these noises also translated to IF 1/f noise here is not problematic because of the low frequency. It is up converted. Going to LO frequency, it is filtered IF filter sets the BW, so only this value is taken from noise (e.g. 30KHz in GSM) When each of the two switches in on instantaneously, noises 4 and 5 and their images contributes to IF When Q2 and Q3 are on simultaneously for a part of a period, the two transistors amplify noises 4 and 5 to the output Noise 6 directly appears at IF frequency April 30, 2017 85 Noise in Mixers Spice Models would not be able to calculate noise of the mixer so: Sine wave sources are used as sources of noise with the same frequency Transient analysis calculates the gain The process is also done at image frequencies Noise gains are added The blue highlighted statement of the previous side is problematic April 30, 2017 86 Intuitive remedies to reduce noise Increasing LO swing is the solution for Q2 and Q3 not being on simultaneously Trying to reduce Cp by reducing the size of Q1,Q2,Q3, lowers noise sources 4 and 5 Cp is the parasitic capacitance arising from the base-emitter junction of Q2 and Q3 and C-B and C-substrate of Q1 For reducing noise 5, larger Q2 and Q3 are effective because of lower rb In Q1, the noise number 2 is equal to 2qIc1 I n 2qI C 1 2 Vn April 30, 2017 2 2qI C 1 2qVT 2 I C1 gm 87 Intuitive remedies to reduce noise Increasing the lower stage current is effective This circuit increases the lower transistor’s current and lowers the collector current of Q2 and Q3 The upper transistors switch better and Q1 introduces lower noise DC source can be made a spike and reject the noise of switching at the switching instant. April 30, 2017 88 New methods to calculate noise of mixers Chris Hull method Harmonic Balance Physical model of “Darabi” April 30, 2017 89 Chris Hull method The circuit is nonlinear when considered totally but at the instant of taking a picture of it, it is linear The circuit is periodically linear relative to LO signal So the impulse response of each noise source is a function of the instant of injecting it at the period of LO For each source of noise there is a three dimensional impulse response including the instant of applying the impulse in LO period After performing two dimensional FFT, for each frequency, the gain is calculated for all of the noise sources The total noise is calculated April 30, 2017 90 Physical model of “Darabi” In Zero-IF 1. 1/f noise of the upper tree leaks to the output with gain 2. 1/f noise of the lower stage leaks to the output at the same condition April 30, 2017 91 Physical model of “Darabi” In Zero-IF, 1/f noise of the upper tree leaks to the output with gain The simultaneous switching of the transistors of the upper tree can be modeled as a DC offset that leads to appearing the RF frequency in the output: COS t DC RF Offset ACOS LO t The equivalent noise of the upper tree April 30, 2017 92 Physical model of “Darabi” Added noise to the LO signal changes the switching point so there will be a new zero-crossing Vn LO +Vout - + LO - gm section April 30, 2017 93 Physical model of “Darabi” April 30, 2017 94 Physical model of “Darabi” April 30, 2017 95 Physical model of “Darabi” April 30, 2017 96 Physical model of “Darabi” Δt Vn Vn S t New zero-crossing A random function with the amplitude of 2IR or -2IR is added to the output April 30, 2017 97 Physical model of “Darabi” iON t 2 I T : the period of T 2 V V 4 I n 4 I n LO ST 2 S LO If LO is a sin with the amplitudeA S 2 A iON LO A sin t LO A sin t Vn LO IV 4I n 2 2 A LO A Vn i 4I 4A ON April 30, 2017 98 Physical model of “Darabi” upper tree as the source of noise: 2 g mVin SNR Vn 4I ST ST g m Vin 2 I Vn In this analysis, only low frequency noise (e.g. 1/f) is considered because it is assumed that the variation of noise is much slower than LO April 30, 2017 99 Physical model of “Darabi” In BJT : Long Channel g m I cte V T g 2 m V I eff In MOS : Short Channel April 30, 2017 V eff Esat L g 2 m 2 V V Esat L I eff eff 100 Physical model of “Darabi” Short Channel : SNRMOS Vin ST 1 2 VGS VT Vn In order to reduce noise: 1. LO must have square wave shape 2. Veff of the lower transistor must be reduced: 3. For gm to remain unchanged, W/L must be increased that causes Cp and 1/f noise of the lower transistor to grow 1/f noise is not important in Low-IF but considerable in Zero-IF 1/f noise of the lower transistor has to be considered as a term added to 1/f noise calculated before April 30, 2017 101 Physical model of “Darabi” To consider the effect of 1/f noise of the upper tree: LO feedthrough can be measured and the value of Voffset that causes the LO feedthrough is calculated Mixer gain ion 1/f noise VOS gm Vni 2A 2 1 f The ratio of equivalent offset voltage and the amplitude of LO April 30, 2017 102 Calculation of Indirect Noise Vn locates itself on Cp and the resulting current is noisy that directly appears at the output that is called “indirect noise” Vn LO+ April 30, 2017 LO- 103 Calculation of Indirect Noise dVCP 2 T2 ion 0 iCP t dt , iCP C P T dt 2 T2 dVA 2 T ion 0 C P dt C P VA VA 0 T dt T 2 2 ion C P Vn T : The noise is slow The noise is called “indirect” because it is converted to the current of capacitor and then transfers to output April 30, 2017 104 Noise in mixers Load noise at IF frequency Thermal noise of the input tr. 2 1 4 KT 2 Vn2 8KTR noise g gm R n L f L m & thermal noise of the Gain of mixer intermedia te stage The effect of Image frequencies+ thermal noise at harmonics n: represents the effect of harmonics 2 1 1 n 2 1 2 2 3 5 4 April 30, 2017 105 Noise in mixers If thermal noise is more important than 1/f noise as in Low-IF: IR 2 2 4 KT Vn2 8KTR 8KT L g 2 gm R n L L m A Thermal noise of upper tree calculated by direct calculation method April 30, 2017 106 Contents 1. 2. 3. 4. 5. 6. 7. 8. 9. Introduction Basic concepts Digital modulation, Spectral control, Detection Multiple access standards, TDM, CDM, OFDM TRx architecture LNA and Mixer Oscillator Frequency Synthesizer Power Amplifier April 30, 2017 107 Oscillator LC vs. VCO Design Phase noise considerations Loop design Inductor limitations Quad signal generation April 30, 2017 108 General Oscillatory System RF oscillator viewed as a feedback circuit Y S H S X S 1 H S if : H S 10 April 30, 2017 The feedback system oscillates 109 General Oscillatory System The output spectrum on the spectrum analyzer looks like: A wideband oscillation will be present on the spectrum April 30, 2017 110 General Oscillatory System Saturation limits the amplitude of oscillation average gain small signal April 30, 2017 111 General Oscillatory System 1. 2. For Oscillation: A start-up signal is required Noise growth has to be limited noise Average loop gain returns to unity Stable amplitude A frequency-selective network called “resonator” is required: 1. 2. To set the frequency of oscillation To reject the harmonics April 30, 2017 112 General Oscillatory System 50-10=40Ω can not oscillate Oscillates but its frequency is unknown a frequency selective circuit is required noise is the start-up signal in large amplitudes the negative resistance reduces 50...... 50 60 55 50 oscillatio n condition nonlinear elements do the function of limiting April 30, 2017 113 ALC A mechanism to define the amplitude of oscillation: April 30, 2017 114 ALC April 30, 2017 115 ALC A detector senses the output signal to be compared with a reference voltage thus the gain of H(S) is controlled The output of this oscillator is a pure sine with minimum harmonics The resonator in oscillating circuits rejects harmonics but in this circuit, the gain is set to unity with control circuit and no harmonic is produced The drawback is that the complexity and phase noise of the control circuit is high April 30, 2017 116 Desired output of an RF oscillator Previously analysis of mixers proved that square wave is ideal as the output of an RF oscillator generally the output of Oscillators are sine waves because of bandwidth limitation Consequently, a large-amplitude sine wave is required to represent a square wave at zero crossing points April 30, 2017 117 LC vs. VCO Following the feedback model, a one-transistor LC oscillator includes an LC tank at the collector with a feedback to base or emitter In resonance, the impedance of the LC tank is real so the phase difference between its current and voltage is zero. For a total phase shift equal to zero, the feedback must compensate for the transistor phase shift. The important issue is that a low resistive load seen at the emitter, 1/gm Reduces the Q of the tank The loop gain drops below unity and oscillation is prevented April 30, 2017 118 LC vs. VCO The solution is transforming the impedance to a higher value before it appears in parallel with the tank April 30, 2017 119 LC vs. VCO A transformer can do the task: The value “ n2⁄gm” is transformed The loop gain is: 2 1 n 1 g m RP g m RP n gm n Reduced loop gain lowers the required nonlinearity to come to the conditions of oscillation RP is the equivalent resistance of the resonator Lower phase noise is obtained April 30, 2017 120 LC vs. VCO Passive impedance transformation is achieved by utilizing tanks with capacitive or inductive dividers Colpitts and Hartley are the examples Colpitts: April 30, 2017 Hartley: 121 LC vs. VCO Different models for implementation C1 C2 C2 C1 April 30, 2017 Butler 122 VCO The circuit in which the output frequency of an oscillator is controlled by a voltage is called Voltage-Controlled Oscillator (VCO) In LC implementations (part of) the tank capacitance can be provided by a reverse-biased diode April 30, 2017 123 VCO Each Diode is actually a varactor but in VCO IC, for achieving higher capacitance a larger Diode is incorporated The nonlinearity of the circuit should not be high Mixing results in transmission of 1/f and thermal noise to RF frequency April 30, 2017 phase noise is generated 124 VCO The operating region of the varactor is before the peak operating region of varactor April 30, 2017 125 VCO The nonlinearity of the varactor's capacitor generates phase noise (the value of it changes in the period of the sine) Two Circuits to reduce the nonlinearity of the varactor are as the following: April 30, 2017 126 LC vs. VCO Colpitts is better accepted because of its only one inductor usage Both of them have two drawbacks: To make the effect of the nonlinear g_m negligible on the Q of the tank we need a large ratio in the tapped inductors or capacitors. Only a single-ended output is provided April 30, 2017 127 VCO The circuit in which the output frequency of an oscillator is controlled by a voltage is called Voltage-Controlled Oscillator (VCO) In LC implementations (part of) the tank capacitance can be provided by a reverse-biased diode April 30, 2017 128 Phase Noise Noise can influence both amplitude and frequency of the oscillator but the latter is more important Random deviation of the frequency is considered: For a nominal periodic sine : n t X t A cos t n t is the small random excess phase representing variation in the period called phase noise For : n t 1 X t A cos C t An t sin C t That is the spectrum of n t is translated to ±ωC exhibiting skirts around the carrier frequency April 30, 2017 129 Phase Noise We consider a unit bandwidth at an offset Δω with respect to ωc and calculate the noise power in this bandwidth and divide the result by the carrier average power Phase noise is dropping of the noise power per hertz with respect to carrier April 30, 2017 130 Importance of phase noise Incorporating an oscillator with a finite phase noise, an adjacent channel with a large interferer and the wanted signal both downconvert with two overlapping spectra The wanted signal is drawn at the skirt of the adjacent channel The wanted signal suffers from noise due to the tail of the interferer April 30, 2017 131 Phase Noise April 30, 2017 132 Driscoll Circuit VB April 30, 2017 133 Driscoll Circuit Minimum phase noise is achieved if: 1. Q of the resonator is high enough 2. Nothing loads the tank (transformer is used) 3. The differential pair acts as a limiter (the whole current is switched to one of the transistors of the differential pair 4. Q1 can become nonlinear but the limiter in diff pair starts limiting long before that. 5. Oscillation is done at the point with maximum slope April 30, 2017 134 Driscoll Circuit 1. 2. 3. 4. A buffer must separate the resonator and the limiter to prevent the Upconversion of 1/f noise Transistors with low thermal and 1/f noise must be selected Symmetric limitation is done. (differential pair is completely symmetric) Soft limiter Sharp limiting is desirable Soft Limiter Soft limiter functions at large Hard Limiter amplitudes causes the Hard limiter elements of the circuit to be nonlinear and causes clipping April 30, 2017 135 Driscoll Circuit Another theory for phase noise reduction states that: The transistor switches on instantly and injects a sharp current in to the resonator thus injected noise is reduced April 30, 2017 136 Quadrature Signal Generation Methods RC/CR +/Divider LLL Quadrature OSC (with feedback loop) April 30, 2017 137 RC/CR The advantage is its simplicity I Q April 30, 2017 138 RC/CR The drawbacks: There is only one frequency in which the amplitudes of I and Q are equal Dependency to the mismatch of R’s and C’s April 30, 2017 139 +/ If addition and subtraction of two vectors are equal then the two vectors are in Quadrature phases I Q April 30, 2017 140 +/ Soft Limiting equalizes the amplitudes without any clipping I Q April 30, 2017 141 divider A master-slave flipflop which divides a signal at 2ω1 by a factor 2, generates Quadrature periodic signals with frequency ω1 Duty cycle is 50% otherwise phase error will happen I Q April 30, 2017 142 divider If the duty cycle of the input is not 50-50, the remedy is: I 2 2 Q But to have the frequency equal to f, a VCO that generates 4f is required April 30, 2017 143 LLL: Level Lock Loop For sine wave input Vref increases up to the value that duty cycles reach to 50% and a 90° phase difference is obtained in + - I ÷2 Q Vref integrator April 30, 2017 Phase detector 144 Quadrature OSC (with feedback loop) Coupling two oscillators in such a way to make them oscillate with 90° difference in phase Measuring the phase difference and controlling the bias current leads to precise 90°-phase shift April 30, 2017 145 Wide tune Range VCO The characteristic curve of a varactor's capacitor looks: C 10 pf 3pf -10v April 30, 2017 0v VC 146 Wide tune Range VCO CV is very nonlinear Having the required voltage range on the IC is not easy. (no -10V on the IC) f 1 2 LC 1 2 LC f C v if Cf 0 if C f C v 10% VCO 40% C v April 30, 2017 10% VCO 20% C v 147 Wide tune Range VCO For wide ranges with no phase noise Cf is varied instead of Cv In the field of instrumentation, VCO‘s with high frequency range is required In these applications the whole band is upconverted to a high frequency and then multiplied by the next mixer Mixing is done in several steps 0 – 10GHz 20 – 30GHz April 30, 2017 20 GHz # 20.2 GHz 200 MHz # 21.4 MHz # 221.4 MHz 148 Wide tune Range VCO 1. 2. 3. 4. Different old IF frequencies: 455KHz : AM 10.7MHz: FM 21.4MHz: Spectrum analyzers 70MHz, 140MHz, 280MHz :Analog satellite April 30, 2017 149