* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Barnett
Diffraction grating wikipedia , lookup
Nonlinear optics wikipedia , lookup
Ultrafast laser spectroscopy wikipedia , lookup
Photonic laser thruster wikipedia , lookup
Upconverting nanoparticles wikipedia , lookup
Neutrino theory of light wikipedia , lookup
Boson sampling wikipedia , lookup
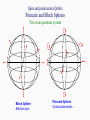
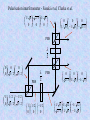
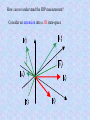
Photons and Quantum Information Stephen M. Barnett 1. A bit about photons 2. Optical polarisation 3. Generalised measurements 4. State discrimination Minimum error Unambiguous Maximum confidence 1. A bit about photons Photoelectric effect - Einstein 1905 eV h W BUT … Modern interpretation: resonance with the atomic transition frequency. We can describe the phenomenon quantitatively by a model in which the matter is described quantum mechanically but the light is described classically. Photons? Single-photon (?) interference - G. I. Taylor 1909 Light source Smoked glass screens Screen with two slits Photographic plate Longest exposure - three months “According to Sir J. J. Thompson, this sets a limit on the size of the indivisible units.” Single photons (?) Hanbury-Brown and Twiss P (1,2) RI TI RT I 2 1 P (1) R I 2 Blackbody light g(2)(0) Laser light g(2)(0) = 1 =2 g ( 2 ) ( 0) P ( 2) T I I2 I Single photon 2 1 g(2)(0) = 0 !!! violation of Cauchy-Swartz inequality Single photon source - Aspect 1986 Detection of the first photon acts as a herald for the second. Second photon available for Hanbury-Brown and Twiss measurement or interference measurement. Found g(2)(0) ~ 0 (single photons) and fringe visibility = 98% Two-photon interference - Hong, Ou and Mandel 1987 “Each photon then interferes only with itself. Interference between different photons never occurs” Dirac 50/50 beam splitter R=T=1/2 P = R T 2 = 1/2 Two photons in overlapping modes Boson “clumping”. If one photon is present then it is easier to add a second. Two-photon interference - Hong, Ou and Mandel 1987 “Each photon then interferes only with itself. Interference between different photons never occurs” Dirac 50/50 beam splitter R=T=1/2 P = R T 2 = 1/2 Two photons in overlapping modes Boson “clumping”. If one photon is present then it is easier to add a second. Two-photon interference - Hong, Ou and Mandel 1987 “Each photon then interferes only with itself. Interference between different photons never occurs” Dirac 50/50 beam splitter R=T=1/2 P = 0 !!! Two photons in overlapping modes Destructive quantum interference between the amplitudes for two reflections and two transmissions. 1. A bit about photons 2. Optical polarisation 3. Generalised measurements 4. State discrimination Minimum error Unambiguous Maximum confidence Maxwell’s equations in an isotropic dielectric medium take the form: E 0 E, B and k are mutually orthogonal B 0 B E t E B 2 c t E S k B For plane waves (and lab. beams that are not too tightly focussed) this means that the E and B fields are constrained to lie in the plane perpendicular to the direction of propagation. 1 0 E B Consider a plane EM wave of the form E E 0 exp i (kz t ) B B 0 exp i (kz t ) If E0 and B0 are constant and real then the wave is said to be linearly polarised. B Polarisation is defined by an axis rather than by a direction: B E E If the electric field for the plane wave can be written in the form E E0 (i ij) exp i(kz t ) Then the wave is said to be circularly polarised. For right-circular polarisation, an observer would see the fields rotating clockwise as the light approached. B E The Jones representation We can write the x and y components of the complex electric field amplitude in the form of a column vector: i E0 x E0 x e x E i y 0 y E0 y e The size of the total field tells us nothing about the polarisation so we can conveniently normalise the vector: Horizontal polarisation Vertical polarisation 1 0 0 1 Left circular polarisation 1 2 1 i Right circular polarisation 1 2 1 i One advantage of this method is that it allows us to describe the effects of optical elements by matrix multiplication: Linear polariser (oriented to horizontal): Quarter-wave plate (fast axis to horizontal): 1 0 0 0 1 1 1 0 , 90 , 45 0 0 0 1 2 1 1 1 0 1 0 0 i 0 , 0 i 90 , 1 i 45 i 1 1 0 0 1 Half-wave plate (fast axis horizontal or vertical): The effect of a sequence of n such elements is: 1 2 A an B c n bn a1 d n c1 b1 A d1 B We refer to two polarisations as orthogonal if E*2 E1 0 This has a simple and suggestive form when expressed in terms of the Jones vectors: A1 A2 B is orthogonal to B if 1 2 A2* A1 B2* B1 0 A * 2 A2 B2 B2* A1 B 0 1 † A1 B 0 1 There is a clear and simple mathematical analogy between the Jones vectors and our description of a qubit. Spin and polarisation Qubits Poincaré and Bloch Spheres Two state quantum system Bloch Sphere Electron spin Poincaré Sphere Optical polarization We can realise a qubit as the state of single-photon polarisation Horizontal 0 Vertical 1 Diagonal up 1 2 Diagonal down 1 2 Left circular 1 2 Right circular 1 2 0 1 0 1 0 i 1 0 i 1 1. A bit about photons 2. Optical polarisation 3. Generalised measurements 4. State discrimination Minimum error Unambiguous Maximum confidence Probability operator measures Our generalised formula for measurement probabilities is P(i) Tr ˆi ˆ The set probability operators describing a measurement is called a probability operator measure (POM) or a positive operator-valued measure (POVM). The probability operators can be defined by the properties that they satisfy: Properties of probability operators I. They are Hermitian II. They are positive III. They are complete ˆ ˆ n † n ˆ n 0 ˆ n Î Observable Probabilities Probabilities n IV. Orthonormal ˆ iˆ j ijˆ i ?? Generalised measurements as comparisons Prepare an ancillary system in a known state: A S Perform a selected unitary transformation to couple the system and ancilla: S+A S S A Uˆ S A A Perform a von Neumann measurement on both the system and ancilla: i Si Ai The probability for outcome i is P(i) i Uˆ A S S A Uˆ † i S A Uˆ † i i Uˆ A S ˆi The probability operators ˆ i act only on the system state-space. POM rules: I. Hermiticity: A Uˆ † i i Uˆ A † ˆ AU i † i Uˆ A II. Positivity: ˆi i Uˆ S A 2 III. Completeness follows from: i i i Î A,S 0 Generalised measurements as comparisons We can rewrite the detection probability as P(i) A S Pˆi S A † ˆ ˆ Pi U i i Uˆ is a projector onto correlated (entangled) states of the system and ancilla. The generalised measurement is a von Neumann measurement in which the system and ancilla are compared. ˆi A Pˆi A ˆ nˆ m A Pˆn A A Pˆm A 0 Simultaneous measurement of position and momentum The simultaneous perfect measurement of x and p would violate complementarity. p Position measurement gives no momentum information and depends on the position probability distribution. x Simultaneous measurement of position and momentum The simultaneous perfect measurement of x and p would violate complementarity. Momentum measurement gives no position information and p depends on the momentum probability distribution. x Simultaneous measurement of position and momentum The simultaneous perfect measurement of x and p would violate complementarity. p Joint position and measurement gives partial information on both the position and the momentum. x Position-momentum minimum uncertainty state. POM description of joint measurements Probability density: ( xm , pm ) Trˆˆ ( xm , pm ) Minimum uncertainty states: xm , pm 2 2 1 / 4 ( x xm ) 2 dx exp 4 2 ipm x x 1 dxm dpm xm , pm xm , pm Î 2 This leads us to the POM elements: 1 ˆ ( xm , pm ) xm , p m xm , p m 2 The associated position probability distribution is ( x xm ) 2 ( xm ) dx x ˆ x exp 2 2 Var ( xm ) x 2 2 2 & Var ( pm ) p 2 4 2 Increased uncertainty is the price we pay for measuring x and p. 1. A bit about photons 2. Optical polarisation 3. Generalised measurements 4. State discrimination Minimum error Unambiguous Maximum confidence The communications problem ‘Alice’ prepares a quantum system in one of a set of N possible signal states and sends it to ‘Bob’ i selected. prob. pi Preparation device ̂ i Measurement device P( j | i) Tr ˆ j ˆ i Bob is more interested in Tr ˆ j ˆ i pi P (i | j ) Tr (ˆ j ˆ ) Measurement result j In general, signal states will be non-orthogonal. No measurement can distinguish perfectly between such states. Were it possible then there would exist a POM with 1 ˆ1 1 1 2 ˆ 2 2 2 ˆ1 2 0 1 ˆ 2 1 Completeness, positivity and 1 ˆ1 1 1 ˆ1 1 1 Aˆ 2 ˆ1 2 1 2 Aˆ positive and Aˆ 1 0 2 2 Aˆ 2 1 2 2 0 What is the best we can do? Depends on what we mean by ‘best’. Minimum-error discrimination We can associate each measurement operator ˆ i with a signal state ̂ i . This leads to an error probability Pe 1 p jTr ˆ j ˆ j N j 1 Any POM that satisfies the conditions ˆ j ( p j ˆ j pk ˆ k )ˆ k 0 N p ˆ ˆ k 1 k k k p j ˆ j 0 will minimise the probability of error. j , k j For just two states, we require a von Neumann measurement with projectors onto the eigenstates of p1 ˆ1 p2 ˆ 2 with positive (1) and negative (2) eigenvalues: Pemin 12 1 Tr p1 ˆ1 p2 ˆ 2 Consider for example the two pure qubit-states 1 cos 0 sin 1 1 2 cos(2 ) 2 cos 0 sin 1 The minimum error is achieved by measuring in the orthonormal basis spanned by the states 1 and 2 . 1 1 2 2 We associate 1 with 1 and 2 with 2 : Pe p1 1 2 2 p2 2 1 2 The minimum error is the Helstrom bound Pemin 1 2 1 1 4 p1 p2 1 2 1/ 2 2 A single photon only gives one “click” P = |a|2 a +b P = | b| 2 But this is all we need to discriminate between our two states with minimum error. A more challenging example is the ‘trine ensemble’ of three equiprobable states: 0 31 1 12 0 3 1 p1 2 12 p2 3 0 1 3 p3 1 3 1 3 It is straightforward to confirm that the minimum-error conditions are satisfied by the three probability operators ˆi 23 i i Simple example - the trine states Three symmetric states of photon polarisation 3 2 3 1 2 3 2 Minimum error probability is 1/3. This corresponds to a POM with elements 2 ˆ j j j 3 How can we do a polarisation measurement with these three possible results? Polarisation interferometer - Sasaki et al, Clarke et al. 1 / 6 2 / 3 1 / 6 0 0 0 0 0 0 1 / 6 1 / 6 2 / 3 PBS 2 0 0 0 0 3 / 2 3 / 2 PBS 1 1 / 2 1 / 2 0 3 / 2 3 / 2 2 11/ 2 1/ 2 0 0 0 PBS 0 0 0 2 / 3 1 / 6 1 / 6 1 / 3 1 / 12 1 / 12 2 / 3 1 / 6 1 / 6 Unambiguous discrimination The existence of a minimum error does not mean that error-free or unambiguous state discrimination is impossible. A von Neumann measurement with Pˆ1 1 1 ˆ P1 1 1 will give unambiguous identification of 2 : result 1 2 error-free result 1 ? inconclusive There is a more symmetrical approach with ˆ1 ˆ 2 1 1 1 2 1 1 1 2 2 2 1 1 ˆ ? Î ˆ1 ˆ 2 Result 1 Result 2 Result ? State 1 1 1 2 0 1 2 State 2 0 1 1 2 1 2 How can we understand the IDP measurement? Consider an extension into a 3D state-space b a a b Unambiguous state discrimination - Huttner et al, Clarke et al. a ? b a b A similar device allows minimum error discrimination for the trine states. Maximum confidence measurements seek to maximise the conditional probabilities P( i | i ) for each state. For unambiguous discrimination these are all 1. Bayes’ theorem tells us that pi i ˆi i pi P(i | i ) P( i | i ) P(i ) k pk k ˆi k so the largest values of those give us maximum confidence. The solution we find is ˆi ˆ ˆ j ˆ 1 1 where ˆ j j j ˆ pi ˆ i i Croke et al Phys. Rev. Lett. 96, 070401 (2006) Example • 3 states in a 2dimensional space • Maximum Confidence Measurement: • Inconclusive outcome needed Optimum probabilities • Probability of correctly determining state maximised for minimum error measurement • Probability that result obtained is correct maximised by maximum confidence measurement: Results: Maximum confidence Minimum error Conclusions • Photons have played a central role in the development of quantum theory and the quantum theory of light continues to provide surprises. • True single photons are hard to make but are, perhaps, the ideal carriers of quantum information. • It is now possible to demonstrate a variety of measurement strategies which realise optimised POMs • The subject of quantum optics also embraces atoms, ions molecules and solids ...