* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Special Segments in Triangles
Line (geometry) wikipedia , lookup
Golden ratio wikipedia , lookup
Dessin d'enfant wikipedia , lookup
Euler angles wikipedia , lookup
Engineering drawing wikipedia , lookup
History of trigonometry wikipedia , lookup
Rational trigonometry wikipedia , lookup
Technical drawing wikipedia , lookup
Trigonometric functions wikipedia , lookup
Euclidean geometry wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Pythagorean theorem wikipedia , lookup
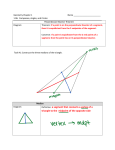
Special Segments in Triangles: Median: Definition – The segment that joins vertex and the midpoint of the opposite side. Drawing – C A B Special characteristics – 1.) Bisects one of the sides of a triangle 2.) Every triangle has three of them. Altitude: Definition – Any line segment from a vertex perpendicular to the base Drawing – (show two triangles….one with the altitude inside, and one with it outside) C C A B A B Special characteristics – 1.) Can be inside or outside the triangle 2.) Every triangle has 3 of them 3.) Forms right angles when vertex is connected with opposites sides segment or segment extended. Perpendicular Bisector: Definition – A line segment that passes through the midpoint of a side of a triangle and is perpendicular to that side. Drawing – C A B Special characteristics – 1.) Bisects one side of the triangle 2.) Each point on the perpendicular bisector is equidistant from the endpoints of the segment. 3.) Every triangle has 3 of them. Angle Bisector: Definition – A line segment that divides an angle of a triangle into two congruent angles. Drawing – C A B Special characteristics – 1.) Every triangle has 3 of them. 2.) Any point on the bisector is equidistance from the sides of the angle.