Download Enzymes: Biological Catalysts

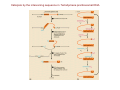
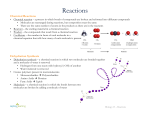
Enzymes: Biological Catalysts
10/11/07
The Role of Enzymes
• A catalyst increases the rate or velocity of a chemical reaction
without itself being changed in the overall process. Most
biological catalysts are proteins called enzymes. The
substance acted on by an enzyme is called a substrate.
Enzymes speed up reactions by many orders of magnitude.
For example, the enzyme catalase speeds up the conversion
of hydrogen peroxide to water and oxygen by a factor of a
billion.
• True catalysts, such as enzymes, participate in the reaction,
but are unchanged by it. Therefore, they can continue to
catalyze subsequent reactions.
• Catalysts change the rates of reactions, but do not affect the
equilibrium of a reaction. i.e., you cannot make more product
from an enzyme-catalyzed reaction than you can from the
same reaction without it. The enzyme simply helps to reach
the equilibrium state faster than if it were not present.
Reaction Order
•
•
•
First order reactions - For the irreversible reaction, A Æ B, the reaction
rate (V) is given by
V = d[B]/dT (for the rate of appearance of the product, B or by
V = -d[A]/dT (for the rate of disappearance of the substrate, A).
These equations are equally valid for this reaction, so
V = d[B]/dT = -d[A]/dT = k1[A],
where k1 is called the rate constant, (seconds)-1. The first-order reaction
called, is due to the first power of the reactant concentration. If k1 is large,
the reaction is fast and if k1 is small, the reaction is slow.
Integrating the above equation yields
[A]/[A]0 = e-(k t), where [A]0 is the starting concentration of A when t = 0.
A plot of this equation (Figure a) shows that the concentration of A
decreases exponentially with time. The amount of time it takes for half of A
to be lost is called the half-life and is given by t1/2. The half-life is inversely
proportional to k1.
A plot of ln[A] vs t, as shown in Figure b, will always yield a straight line with
slope = -k1 if the reaction is first order. If one plots the initial rate of the
reaction versus varying starting concentrations ([A]0), a straight line plot with
slope of k1 will be produced for a first order reaction. The most common
example of a first order reaction is the decay of radioactive elements.
1
•
•
Determining the order and rate constant of an irreversible firstorder reaction.
The equilibrium does not lie far to one side and, as product accumulates, the
reverse reaction becomes important. So, for the reaction A kk1 B, a forward
-1
reaction constant, k1, can be used to define the reaction moving rightward and a
reverse reaction constant, k -1 can be used to define the reaction moving
leftward. Now the molecule A is being consumed in the reaction to the right and
formed by the reaction to the left, so the corresponding rate equation is
-V = d[A]/dt = -k1[A] + k-1[B]
Such a reaction approaches a state of equilibrium, at which point the rates of
the forward and reverse reactions become equal. At the same time, the overall
rate becomes zero, so
0 = -k1[A]eq + k-1[B]eq or [B]eq/[A]eq = k1/k-1 = K,
where K is the equilibrium constant. For a reversible reaction that is first-order
in both directions, the equilibrium constant is always the ratio of the forward and
reverse rate constants.
Reaction Order
• Second-Order Reactions - A reaction of this type typically
occurs when two molecules come together to form products. A
simple example is
k2
2A Æ A2
• with a rate constant given by k2. The rate of such a reaction is
proportional to the second power of the concentration of the
reactant. Therefore, V = -d[A]/dt = -k2[A]2
• Here k2 is the second-order rate constant. It has dimensions of
(mol/L)-1s-1 or M-1s-1
Transition States and Reaction Rates
• The below Figure depicts a plot of the free energy of
the system versus the reaction coordinate for a
chemical reaction. This simplistic view illustrates
that the standard state free energy of the products is
lower than that of the reactants. It shows little of
what happens in the transition from reactant to
product.
• Reactions do not occur all at once. A molecule in a
first-order reaction must only occasionally reach an
energy state in which the process can occurotherwise all molecules would react at once. In
reality, only a certain fraction of the molecules which
are sufficiently energetic can undergo reactions.
The same is true in second order reactions
Reactions have free energy "barriers" to them. An activated or "transition
state" for a molecule occurs when it has reached an energy that is sufficient
to react. Figure b more accurately depicts the free energy barrier for a
reaction. Figure c shows the same conversion for an actual molecular
alteration-a boat Æ chair conversion of a pyranose ring. Here the transition
state is drawn as a half-boat/half-chair structure.
As shown in Figures b and c, the transition state (symbolized by ‡ )
represents an intermediate molecular state having an increase in free energy
of ΔG1o‡ above that of the initial substrate. If the barrier to reaction is high,
only a small fraction of the molecules will have enough energy to react.
•
If let [A]‡ represent the concentration of molecules having the activation
energy, then we can write the equilibrium constant K as [A]‡ /[A]. Substituting
into equation 3.23,
we obtain
[A] = [A]e-
/RT
Because only molecules at the transition state can proceed to react (in either
direction), the rate constant can be then expressed as proportional to the
population of the transition state:
,
where Q represents the frequency of forming the product (right side of reaction equation).
Substituting ΔG1o‡ = ΔHo‡ - TΔSo‡ , we obtain
which is known at the Arrhenius equation. Q' is a constant equal to
Q’ = Qe(ΔSo‡/R)
so we take the natural logarithms of both sides and simplify to obtain
Since we expect ΔH。‡ to be positive, reactions should go faster at higher
temperatures. From equation 11.11, a graph of ln k versus 1/T should be a straight
line and its slope should give Δ H。‡ . An example (the reaction of L-malate to yield
fumarate and water) is shown in Figure below.
The activation energy opposes the reaction in both directions, with
ΔG1o‡ and ΔG-1o‡ representing the transition state free energy barrier in the
forward and reverse directions, respectively. Incorporating this and K = k1/k-1,
-
=
,
Thus, the equilibrium constant K tells nothing about the rates of process. K depends
only on the free energy difference between final and initial states and carries no
information about the height of the barrier between these states.
Summary of important points:
1. Reactions should go faster at higher temperatures.
2. The activation energy opposes the reaction in both directions.
3. K reveals nothing about the rates of process-it depends only on the free energy
difference between final and initial states and carries no information about the height
of the barrier between these states.
How Catalysts Work
•
•
A catalyst works simply by lowering the energy barrier of a reaction. By doing so,
the catalyst increases the fraction of molecules that have enough energy to attain
the transition state, thus making the reaction go faster in both directions.
The position of the equilibrium (the amount of product versus reactant) is
unchanged by a catalyst. Even though k1 and k-1 many be greatly changed from
their values in the absence of a catalyst, each one changes by the same factor and
the equilibrium constant, K, is unchanged, because K = k1/k-1.
Catalysts lower the energy barrier in two ways:
1. The catalyst binds a substrate in an intermediate conformation that
resembles the transition state, but has a lower energy. This may lead to
multiple intermediate states that bypass the transition state. An intermediate
state is a metastable state of a molecule.
2. In a non-catalyzed reaction the entropy may be
highly negative due to the highly specific
orientation required in order for a reaction to occur.
(Note that a more negative entropy contributes to a
more positive free energy of transition.) Catalysts
can lower the negative entropy by binding reacting
molecules only in the proper mutual orientation,
thus increasing their reactivity.
The Induced Fit Model
•
•
The induced fit model of enzyme action is a modification of the lock-andkey model originally proposed by Emil Fischer in 1894. The lock-and-key
model proposes that an enzyme/substrate pair is like a lock and key. Though
it explains the specificity of enzyme/substrate pairs, it does little to explain
catalysis, because a lock does not change a key the way an enzyme
changes a substrate.
In 1958, Daniel Koshland proposed the induced fit model to explain
enzymatic catalysis. The model proposes that distortion of the enzyme and
the substrate is an important event in catalysis.
Figure below shows x-ray diffraction studies of the enzyme hexokinase both
without (a) and with (b) glucose bound. Note that binding of glucose causes
two domains of the enzyme to fold toward each other.
Enzymes do more than simply bind and position substrates, however.
Enzymes
1. Bind substrate(s);
2. Lower the energy of the transition state; and
3. Directly promote the catalytic event.
The latter may occur as a result of specific amino acid side chains that
physically interact with the substrate and end up promoting the reaction.
When the catalytic process is complete, the enzyme must be able to release
the product or products and return to its original state for another round of
catalysis.
For an enzyme (E) that catalyzes the conversion of a single substrate (S)
into a single product (P), the simplest way to write the overall reaction is in
two steps:
S + E <=> ES
ES Æ E + P
Here, ES represents the enzyme-substrate complex. For simplicity, the first
reaction is shown as reversible, while the second reaction is irreversible. For
specific examples, see the triose phosphate isomerase and serine
proteases below.
Triose Phosphate Isomerase Catalysis
•
•
•
Triose phosphate isomerase catalyzes the following reaction:
Glyceraldehyde-3-Phosphate (G3P) <=> cis-enediol intermediate <=>
Dihydroxyacetone Phosphate (DHAP)
As the reaction is written, consider G3P as the substrate and DHAP as the product.
The enediol intermediate is unstable and normally has a much more positive free
energy than either G3P or DHAP.
The active enzyme is a dimer of two identical subunits. Each has the configuration
shown in Figure a. The active site (the place on the enzyme where catalysis occurs)
can accommodate either G3P or DHAP. At the active site, a glutamate residue (Glu
165) and a histidine (His 95) are essential for function of the enzyme. After binding,
an enzyme "lid" closes down on the substrate to provide a cage that protects the
enediol intermediate. In the absence of the lid, the enediol intermediate is lost and
catalytic efficiency decreases by a factor of 100,000. Conversion of Glu 165 to Asp
retains the negative charge, but reduces efficiency by a factor of 1000. The reaction
can be broken down into the following steps:
E + G3P <=> E-G3P (Binding of G3P)
E-G3P <=> E-ed (Conversion to enediol)
E-ed <=> E-DHAP (Conversion to DHAP)
E-DHAP <=> E + DHAP (Release of DHAP)
Like other enzymes, triose phosphate isomerase lowers the energy barriers of the
transition states.
Triose phosphate isomerase is an extremely efficient enzyme.
Serine Protease Catalysis
•
Serine proteases are enzymes that catalyze the hydrolysis of peptide
bonds. In each case, the enzymes have a serine residue that plays a critical
role in the catalysis. The enzymes cuts preferentially in distinct sites. The
active site regions of all of the serine proteases have a number of common
factors. For example, an aspartate residue, a histidine residue, and a serine
residue are always clustered about the active site depression. Such a
structure for chymotrypsin is shown in below Figure. Also, a "pocket" is
always located close to the active site serine.
Active site pockets of two serine proteases.
•The shape and charge of the "pocket," however, vary between different
serine proteases. Thus, it is the nature of the pocket that gives a serine
protease its specificity. For example, in chymotrypsin, the pocket is wide
and lined with hydrophobic residues to accommodate a hydrophobic side
chain, such as phenylalanine.
The catalytic mechanism of chymotrypsin, a serine protease is shown in nest slide.
These steps include the following:
1. Polypeptide substrate binding.
2. Proton transfer from Ser to His. The substrate forms a tetrahedral transition
state
with the enzyme.
3. Proton transfer to the C-terminal fragment, which is released by cleavage of the C-N
bond. The N-terminal peptide is bound through acyl linkage to serine.
4. A water molecule binds to the enzyme in place of the departed polypeptide.
5. The water molecule transfers its proton to His 57. Again, a tetrahedral transition state
is formed.
6. The second peptide fragment is released. The acyl bond is cleaved, the proton is
tranferred from His back to Ser, and the enzyme returns to its initial state.
A key to the mechanism of serine protease catalysis lies in the stability of the two
tetrahedral intermediate states, which are very similar to the essential transition states.
They appear to be stabilized by hydrogen bonds from backbone amino protons from
residues Ser 195 and Gly 193 to one of the oxygens in the tetrahedral complex (the
carbonyl oxygen of the substrate). The hydrogen bonding can occur only with formation
of the tetrahedral state and thus stabilizes the intermediates.
Both triose phosphate isomerase and serine proteases have a histidine and an acidic
residue in their active site. Histidine is very common in active sites, because it readily
accepts or donates protons at physiological pH.
Catalysis of peptide bond hydrolysis by chymotrypsin.
Michaelis-Menten Kinetics
• Equation above represents the minimal equation needed to describe
a simple one-substrate, one-product reaction catalyzed by an
enzyme.
• This assumes the reverse reaction between E and P is negligible and
is a simple, first-order reaction whose rate is determined by [ES] and
the value of k2. The reaction rate can be written as V = k2[ES]
• [ES] is not a measurable concentration. Measurable items are the [S]
and [E]t , which is the sum of the free enzyme and complexed
enzyme. i.e. [E]t = [E] + [ES]
• It is incorrect to assume that E and S are in equilibrium with ES,
because some ES is continually being drained off to make P.
• Briggs and Haldane assumes that when the reaction is started by
mixing enzymes and substrates, the ES concentration builds up at
first, but quickly reaches a steady state, in which it remains almost
constant. The steady state will persist until almost all of the substrate
has been consumed. If one measures rates only after the steady
state has been established and before [ES] has changed much,
reaction velocity can be calculated by assuming steady state
conditions.
The steady state in enzyme kinetics.
In the steady state, rates of formation and breakdown of ES are equal,
Rearranging 11.17 gives equation 11.18,
Combining the three rate constants into one, KM, yields
KM = (k-1 + k2)/k1
Equation 11.18 becomes: KM[ES] = [E][S]
Because [E] = [E]t - [ES], KM[ES] = [E]t[S] - [ES][S]
Solving for [ES], [ES] = [E]t[S]/(KM+[S])
Substituting this into the earlier velocity equation,
V = k2[E]t[S]/(KM+[S])
This is the Michaelis-Menten equation, and KM is called the Michaelis
constant. KM has units of concentration and, because it is a ratio of the rate
constants of a reaction, KM is characteristic of the reaction.
a plot of velocity (V) versus substrate concentration ([S])
Note that at high substrate concentrations ([S] >> KM), the velocity approaches
a maximum (called Vmax). Note also that the substrate concentration where
V = Vmax/2 corresponds to the KM.
At Vmax, [S] >> KM, so [S] + KM ≒ [S]. Thus, the velocity equation simplifies to
Vmax = k2[E]t
Substituting this back into the velocity equation yields
V = Vmax[S]/(KM + [S])
k1
k2
E+S
ES
E+P
k-1
Vmax = k2[E]t
V = k2[ES]
V = Vmax[S]/(KM + [S])
[E]t = [E] + [ES]
Ks = k-1/k1 = [E][S]/[ES]
k1[E][S] = k-1[ES] + k2 [ES]
[ES] = (k1/(k-1 + k2)) [E][S]
KM = (k-1 + k2)/k1
KM[ES] = [E][S]
KM[ES] = [E]t[S] – [ES][S]
[ES](KM +[S]) = [E]t[S]
[ES] = [E]t[S]/(KM +[S])
V = k2[E]t[S]/(KM + [S])
(d[ES]/dt = k1[E][S]-k-1[ES]-k2[ES])
(In a steady state, d[ES]/dt = 0)
For a multistep reaction, the Michaelis-Menten equation must be modified.
Consider the reaction
For this reaction, the k2 in the Michaelis-Menten equation must be replaced by
a more general constant, called kcat. Here,
V = kcat[E]t[S]/( KM + [S])
kcat incorporates the rate constants for all the reactions between ES and E + P.
For the two-step reaction above, kcat = k2.
For more complex reactions, kcat depends on which steps in the process are
rate-limiting.
KM, kCAT, and kCAT/KM
•
For reactions obeying Michaelis-Menten kinetics, KM is a measure of the
substrate concentration required for effective catalysis to occur (the affinity
of the enzyme for substrate ). i.e., an enzyme with a high KM requires a
higher substrate concentration to achieve a given reaction velocity than an
enzyme with a low KM. Table below lists values of KM, kcat, and kcat/KM for
selected enzymes.
kcat Æ V = kcat[E]t[S] / ( KM + [S]) (11.27)
kcat gives a direct measure of the catalytic production of product under
optimum conditions (saturated enzyme). The units of kcat are second s-1. The
reciprocal of kcat can be thought of as the time required by an enzyme
molecule to "turn over" one substrate molecule. Alternatively, kcat measures
the number of substrate molecules turned over per enzyme molecule per
second. Thus, kcat is sometimes called the turnover number.
kcat/KM Æ a measure of enzyme efficiency. Either a large value of kcat (rapid
turnover) or a small value of KM (high affinity for substrate) makes kcat/KM
large.
When [S] << KM (dilute solution), V≒ (kcat/KM)[E][S]
Here, kcat/KM behaves as a second-order rate constant for the reaction
between substrate and free enzyme. This ratio is important, for it shows what
the enzyme and substrate can accomplish when abundant enzyme sites are
available, and it allows direct comparison of the effectiveness of an enzyme
toward different substrates. When an enzyme has a choice of two substrates,
A or B, present at equal, dilute concentrations,
Table shows that when an enzyme has different substrates on which it can
work. Note that for chymotrypsin the kcat/KM ratio varies 1-million fold.
As a second-order rate constant, kcat/KM has a maximum possible value,
which is determined by the frequency with which enzyme and substrate
molecules can collide. A reaction which attains such a velocity is said to be
"diffusion-limited" because every encounter leads to reaction. If every collision
results in formation of an enzyme-substrate complex, diffusion theory predicts
that kcat/KM will attain a value of about 108 to 109 (mol/L)-1s-1. The enzymes
carbonic anhydrase, fumarase, and triose phosphate isomerase actually
approach this limit.
Analysis of Kinetic Data
•
•
To test whether an enzyme-catalyzed reaction follows the Michaelis-Menten
law, the initial rates of a series of reactions are measured (all at the same
enzyme concentration, but at different substrate concentrations). Because
the initial [S] is known precisely, and the change in [S] versus t is almost
linear in the initial stages, accurate data for V as a function of [S] can be
obtained.
A Lineweaver-Burk plot is obtained by inverting the Michaelis-Menten
equation to obtain the following:
A Lineweaver-Burk plot.
For a reaction obeying Michaelis-Menten kinetics, plotting 1/V versus 1/[S]
should yield a straight line. Vmax and KM can be obtained from such a plot.
An Eadie-Hofstee plot.
A disadvantage of the Lineweaver-Burk plot is the long extrapolation
necessary to determine KM. One way around this problem is to graph V
versus V/[S] (called an Eadie-Hofstee plot). The result also yields a straight
line for reactions obeying Michaelis-Menten kinetics. Here, the slope of the
line is equal to -KM.
Multisubstrate Reactions
•
Proteolysis involves two substrates (the polypeptide and water) and two
products (the two fragments of the cleaved polypeptide chain).
• When an enzyme binds two or more substrates and releases multiple
products, the order of the steps becomes an important feature of the enzyme
mechanism. Several classes of mechanisms include the following:
1. Random substrate binding - In this mechanism, either substrate can be
bound first, though in many cases one substrate will be favored for initial
binding, and its binding may promote the binding of the other. The general
pathway is
The phosphorylation of glucose by ATP, catalyzed by hexokinase, appears
to follow this mechanism, with some tendency for glucose to bind first.
2. Ordered substrate binding - This mechanism occurs when one substrate must
bind before a second one can bind significantly. This mechanism is
Ordered substrate binding is often observed in oxidations of substrates by
the coenzyme nicotinamide adenine dinucleotide (NAD+).
3. The "ping-pong" mechanism - This occurs when a catalytic sequence
of events occurs, such as one substrate is bound, one product is released,
a second substrate is bound, and a second product is released. This is
shown as
where E* is a modified form of the enzyme, often carrying a fragment of the first
substrate, S1. A good example is the cleavage of a polypeptide chain by a serine
protease, such as trypsin or chymotrypsin. The polypeptide is described here as S
= A.B, where A and B designate the C-terminal and N-terminal portions of the
chain from the point of cleavage:
Here E*.B and E*.B.H2O indicate covalent intermediates, as in Figure below.
Kinetics of a Complex Reaction - For the cleavage of a substrate by a
serine protease, such as chymotrypsin, the step E*.B + H2O Æ E*.B.H2O
cannot be analyzed. Since the concentration of water is essentially fixed in
aqueous solution and is not a variable, the reaction can be written as
Steady state measurements in this case will be insufficient. The steady
state velocity is given by
The enzyme obeys Michaelis-Menten kinetics, but kcat, KM, and Ks are
defined as
kcat = k2k3/(k2 + k3)
KM = Ksk3/(k2 + k3)
Ks = k-1/k1
Thus, the Michaelis-Menten equation describes the velocity correctly, but the values of
kcat and KM depend on the reaction mechanism. To obtain the individual rate constants
in such a case, measurements outside the steady state range must be employed. The
kinetics of the hydrolysis of esters by chymotrypsin (the enzyme also works on esters)
reveals a rapid concentration increase for a few minutes until about one molecule has
been produced per enzyme molecule. Steady state production begins after that point.
The initial burst is called pre-steady state production. For ester hydrolysis, k3 is much
smaller than k2. Thus, the acyl intermediate forms quickly on each enzyme molecule,
with accompanying release of product A. After this period, however, more A can be
formed only after each acyl intermediate breaks down and the enzyme becomes
available again. The dissociation of the acyl intermediate is the rate-limiting step.
Faster measurement techniques, such as stopped-flow methods, allow
measurement of the rate of formation of the ES complex. Measurements of the
decay of the acyl intermediates after substrate is exhausted provide k3.
Combinations of these methods can be used to obtain all of the constants in
equation 11.34. Example rate constants for hydrolysis of two N-acyl amino acid
esters by chymotrypsin are given in Table.
Enzyme Inhibition
•
Many different kinds of molecules inhibit enzymes and the inhibition may be
reversible or irreversible. Reversible inhibition involves noncovalent binding
of the inhibitor and can always be reversed by removal of the inhibitor.
Irreversible inhibition involves a covalent binding of a molecule to the
enzyme, which incapacitates it.
Reversible Inhibition
• Competitive inhibition - the inhibiting compound so closely resembles
the substrate for the enzyme that it accepts the molecule to the substrate
binding site. However, once bound, the inhibitor cannot be acted on and
thus prevents the enzyme from catalyzing the intended reaction. This
reaction scheme is depicted as
I stands for the inhibitory compound and KI is the dissociation constant for
inhibitor binding -KI = [E][I]/[EI].
Now, [E]t = [E] + [ES] + [EI],
where [EI] is the concentration of inhibitor-enzyme complex.
Then, the velocity is
where
is the apparent KM given by
= KM(1 + [I]/KI)
Increasing [I] causes an apparent increase in the KM. The Vmax is
unchanged, because as [S] increases relative to a fixed [I], the substrate
molecules outcompete the inhibitor for the enzyme's active site.
The effect of a competitive inhibitor on a graph of V versus [S] is shown in
Figure a. The system still obeys an equation of the Michaelis-Menten form at a
given [I], so the Lineweaver-Burk and Eadie-Hofstee plots are linear, but the KM
is altered (Figure b). By plotting the apparent KM as a function of [I] (Figure 1c),
one can obtain both KM and KI.
A variant of competitive inhibition is nonproductive binding. This occurs when a
substrate molecule can fit into the enzyme's second binding site in such a way
that the normal catalytic event cannot occur. This scheme is as follows:
Here, ES' is the enzyme-substrate complex that cannot lead to product. In this
situation, both KM and kcat are modified.
Noncompetitive inhibition - This occurs when a molecule or an ion binds to a site on
the enzyme other than the active site and modifies kcat (Figure 11.22). Such a
compound need not resemble the substrate at all. In fact, it only needs to have a
strong affinity for the second binding site. Assuming the inhibitor has equal affinity for
E and ES, the scheme is
Noncompetitive inhibition.
Mathematical analysis yields equation 11.38.
the KM is unaffected, but the apparent kcat is now given by
kappcat=kcat/([1+[I]/KI]).
The apparent kcat decreases with increasing [I]. Vmax is also changed (Figure
11.23a):
Vappmax=kcat(apparent)[E]t = kcat[E]t/(1 + [I]/KI)
The effect of noncompetitive binding on a Lineweaver-Burk plot is shown in
Figure 11.23b. Both the true kcat and KI are determined by graphing
1/Vappmax versus [I] (Figure 11.23c).
Effects of noncompetitive inhibition on enzyme kinetics.
The situation is usually more complex than shown here. For example, the
complex ESI may also be able to undergo the catalytic process slowly, or the
binding of inhibitor may modify both kcat and KM. The latter case is called
mixed inhibition.
Irreversible Inhibition
•
•
Irreversible inhibition occurs when substances combine covalently with
enzymes so as to inactivate them irreversibly. Almost all irreversible enzyme
inhibitors are toxic substances, either natural or synthetic. Some, such as
cyanide and penicillin, are shown in next slide. Figure in next slide depicts
the action of the competitive irreversible inhibitor, diisopropyl
fluorophosphate (DFP), which reacts with serine groups on a protein to form
a covalent adduct.
Irreversible inhibitors that strongly resemble the substrate rather than its
transition state may be extremely selective. An example is TPCK in next
slide, which is an excellent inhibitor for chymotrypsin. When selective
irreversible inhibitors are used to label active site residues of an enzyme to
aid in their identification, they are called affinity labels. A suicide inhibitor,
on the other hand, is an affinity label that is unreactive until it is acted upon
by the enzyme, at which point it binds.
Irreversible inhibition by adduct formation.
Function of Coenzymes
A protein may require the help of some other small molecule or ion to carry out
the reaction. Molecules bound to enzymes for this purpose are called
coenzymes. The water soluble vitamin B complexes are metabolic precursors
of a number of coenzymes. Table lists several important coenzymes together
with their related vitamins.
NAD+ - Nicotinamide adenine dinucleotide (NAD+) is derived from the vitamin niacin.
The nicotinamide portion of the molecule is capable of being reduced and can thus
serve as an oxidizing agent, where 'R' stands for the remainder of the molecule.
NAD+/NADH behave both like a second substrate in a reaction (because each is
converted to the other by the enzyme) and like a coenzyme (because they are recycled
over and over). They are generally classified as coenzymes
Metal Ions in Coenzymes - Many enzymes contain metal ions, usually held by
coordinate covalent bonds from amino acid side chains, but sometimes bound
by a prosthetic group like heme. Such enzymes are called metalloenzymes.
Figure below shows the active site of the protease carboxypeptidase A, which
contains a zinc ion.
Classification of Protein Enzymes
1.
2.
3.
4.
5.
6.
The Enzyme Commission (EC) of the International Union of Biochemistry
and Molecular Biology (IUBMB) devised a naming and numbering system.
Eenzymes are divided into six major classes, with sub-groups and subsubgroups to define their functions more precisely. The major classes are as
follows:
Oxidoreductases catalyze oxidation - reduction reactions.
Transferases catalyze transfer of functional groups from one molecule to
another.
Hydrolases catalyze hydrolytic cleavage.
Lyases catalyze removal of a group from or addition of a group to a double
bond, or other cleavages involving electron rearrangement.
Isomerases catalyze intramolecular rearrangement.
Ligases catalyze reactions in which two molecules are joined.
The EC of the IUBMB has given each enzyme a number with four parts,
such as EC 3.4.21.5. The first three numbers define major class, subclass,
and sub-subclass, respectively. The last is a serial number in the subsubclass, indicating the order in which each enzyme is added to the list,
which is continually growing. For example, triose phosphate isomerase is
listed as EC 5.3.1.1. Thus, it is an isomerase and in the third subclass
(enzymes that involve an oxidation in one part of the substrate molecule and
reduction in another). It is in the first sub-subclass (those that interconvert
aldoses and ketoses) and is the first entry (of 19 so far) in this sub-subclass.
Molecular Engineering
Molecular engineering is a term used to describe the design of
enzymes using modern molecular biological techniques to alter their
catalytic action. Examples include the following:
• Site-directed mutagenesis - The DNA coding sequence for an enzyme
is altered to change one or more amino acids in an enzyme when the
mutated DNA is expressed in an organism.
• Hybrid enzymes - Molecular techniques are used to put together two
different biomolecules to make a fusion molecule with new, useful
properties. Figure in next slide depicts a hybrid enzyme made in this
fashion. In this case, an oligonucleotide of a defined sequence has been
grafted onto the enzyme staphylococcal nuclease. The specific
sequence in the hybrid enzyme allows it to bind to a specific
complementary nucleic acid sequence (specified by the bound
oligonucleotide) and cut specifically at that point. The native, unaltered
enzyme has no such specificity.
• Catalytic antibodies - Antibodies have a very specific binding site to the
transition state of an enzymatic reaction. The resulting molecules, called
abzymes, act like antibodies. In some cases, abzymes can speed up
reaction rates as much as 107-fold over the uncatalyzed reaction. The
stereospecificity of enzymes (including abzymes) may provide a
tremendous aid to the synthesis of stereospecific compounds in organic
chemistry.
A hybrid enzyme.
Ribozymes
•
Some RNA molecules, called ribozymes are capable of catalyzing chemical
reactions too. Figure 11.29 shows the site of action of the RNA-protein
complex called ribonuclease P. The RNA portion of the complex can, by
itself, catalyze the hydrolysis of the specific bond indicated by the red wedge
in the figure.
Tom Cech identified an interesting protein-independent self-splicing agent from
the preribosomal RNA of the protist, Tetrahymena. In this reaction, the rRNA
itself catalyzes removal of an RNA intron from itself. The RNA molecule
involved in the catalysis is altered, so it is not technically considered a catalyst,
but the sequence which is removed (called L-19 IVS) does have true catalytic
activity. It can either lengthen or shorten small oligonucleotides, in the manner
shown in next slide.
Catalysis by the intervening sequence in Tetrahymena preribosomal RNA.
Regulation of Enzyme Activity
•
Coordinating and regulating enzymatic activities is essential for efficient
functioning of cells. Several control mechanisms that do not involve covalent
modification of the enzymes are possible:
1. Substrate level control - High levels of the product of a reaction inhibit the
ability of the small amounts of substrate present to react. An example is the
first step in glycolysis, catalyzed by hexokinase. It is inhibited by the product
of its action, glucose-6-phosphate. If glycolysis is blocked for any reason,
glucose-6-phosphate accumulates.
2. Feedback control - The product of a series of reactions inhibits the action of
an earlier step in the process (usually the first step). Feedforward regulation
occurs when a molecule in an assembly line reaction activates an enzyme
ahead of it in the pathway.
3. Allosteric enzymes - These enzymes are invariably multisubunit proteins,
with multiple active sites. They exhibit cooperativity in substrate binding
(homoallostery) and regulation of their activity by other, effector molecules
(heteroallostery).
Homoallostery - The effects of cooperative substrate binding on enzyme kinetics are
shown in Figure. Binding of one substrate favors binding of additional substrates.
Cooperative binding favors reduction of KM for the binding of substrates after the
initial one.
The Figure shows the effect of extreme homoallostery. At concentrations of S below
a critical point, [S]c, the enzyme is almost inactive, but then changes activity rapidly
with concentrations of S greater than [S]c.
Heteroallostery - This type of allosteric control involves heteroallosteric effectors which
may be either inhibitors or activators of binding. If an enzyme can exist in two
conformational states, T and R, that differ dramatically in the strength with which
substrate is bound or which differ significantly in the catalytic rate, then the kinetics of
the enzyme can be controlled by any other substance that, in binding to the protein,
shifts the T<==>R equilibrium. Allosteric inhibitors shift the equilibrium toward T and
activators shift it toward the R state.
The Figure illustrates a V-vs-[S] curve. Note that shifts toward the R state (activators)
increase the velocity for a given substrate concentration, whereas shifts toward the T
state have the opposite effect.
Aspartate Carbamoyltransferase
•
Aspartate carbamoyltransferase (also known as aspartate
transcarbamoylase or ATCase) is known for its allosteric regulation:
Aspartate + Carbamoyl Phosphate <==> Carbamoyl Aspartate
ATCase is at the crossroads of biosynthetic pathways that lead to proteins
or pyrimidines. ATCase catalyzes the joining of aspartate and carbamoyl
phosphate to form N-carbamoyl-L-aspartate, the first metabolite committed
to the synthesis of pyrimidines. The enzyme is sensitive to feedback
inhibition by cytidine triphosphate (CTP), and is activated by ATP.
Control points in pyrimidine synthesis.
Regulation of aspartate carbamoyltransferase by ATP and CTP.
Allosteric regulation of ATCase involves changes in the quaternary structure of
the molecule. A major rearrangement of subunit positions occurs in the TÆ R
transition.
Quaternary structure of aspartate carbamoyltransferase (ATCase).
ATCase is a multisubunit protein
consisting of 6 catalytic subunits
and 6 regulatory subunits.
(The quarternary structure of
ATCase enzyme is shown).
The detailed structure of one catalytic subunit (green) and adjacent
regulatory subunit (yellow) of ATCase.
Sometimes different organisms regulate similar pathways in different ways.
For example, ATCase is the major control point in the pyrimidine pathway
synthesis in bacteria, whereas eukaryotes regulate the synthesis of
carbamoyl phosphate. In mammals, the carbamoyl phosphate synthetase
II is inhibited by UDP, UTP, CTP, dUDP, and UDP-glucose.
Covalent Modifications to Regulate Enzyme Activity
•
•
•
Covalent modification activates some enzymes and inactivates others. i.e.
some enzymes are wholly inactive until they are covalently modified and
then begin to function. In other cases, covalent modification acts in the
opposite direction, to inactivate otherwise active enzymes. Some such
modifications can be reversed; others cannot.
One of the most widespread modifications is phosphorylation or
dephosphorylation of various amino acid side chains (e.g., serine,
threonine, tyrosine, and histidine). These kinds of modification are most
often a part of complex regulatory pathways, frequently under hormonal
control.
Proteolytic cleavage, eg. pancreatic proteases (such as trypsin,
chymotrypsin, elastase, and carboxypeptidase): They are made as longer,
catalytically inactive molecules called zymogens (trypsinogen,
chymotrypsinogen, proelastase, and procarboxypeptidase, respectively).
The zymogens must be cleaved proteolytically in the intestine to yield the
active enzymes. If a small amount of protease becomes active in the
pancreas, it can have painful or fatal consequences (i.e., acute pancreatitis).
The pancreas protects itself from active protease action by synthesis of a
protein called the secretory pancreatic trypsin inhibitor. The binding between
trypsin and its inhibitor is one of the strongest noncovalent interactions
known in biochemistry. The intestinal tissue is protected from damage by
proteases by its glycosylated surface.
Zymogen activation by proteolytic cleavage.
The first step is activation of trypsin in the duodenum. A hexapeptide is removed from
the N-terminal end of trypsinogen by enteropeptidase, a protease secreted by
duodenal cells. This yields active trypsin, which then activates the other zymogens by
specific proteolytic cleavages. Trypsin will also activate other trypsinogen molecules in
an autocatalytic process. Activation of a few trypsinogens ultimately leads to activation
of many trypsins.
Activation of chymotrypsinogen is shown in next slide. First, trypsin cleaves the bond
between arginine 15 and isoleucine 16. Notice that the N-terminal peptide remains
attached to the rest of the molecule due to the disulfide bond between residues 1 and
122. The enzyme is activated by the cleavage due to changes in the conformation of
the molecule. These include:
1. Creation of a new, positively charged N-terminal residue at Ile 16;
2. Salt bridge formation between Ile 16 and Asp 194 (next to the active site);
3. Movement of active site residues so that the amino groups of residues 193 and 195
are properly positioned to hydrogen-bond to the substrate oxyanion in the tetrahedral
transition state.
4. Autocatalytic cleavages to remove residues 14-15 and 147-148 from the molecule
produce the final, active form of chymotrypsinogen, called -chymotrypsin.
Activation of chymotrypsinogen.
Blood Clotting
• Blood clots are composed of striated fibers of a protein called
fibrin. Fibrin fibers are derived from a zymogen precursor,
called fibrinogen, by proteolytic cleavages that release
fibrinopeptides A and B from the molecule. Removal of these
small fibrinopeptides exposes sites in the fibrin molecules that
allows them to stick together. Covalent cross-links between
glutamine and lysine residues also form to help stabilize the
structure. Thus, activation of zymogens is a key aspect to
clotting of blood in vertebrates.
1.
2.
3.
4.
5.
6.
7.
8.
production of fibrin is the product of action of a cascade of
proteases as follows:
In damaged tissue, the proteins kininogen and kallikrein activate
factor XII (part of the intrinsic pathway).
Factor XII activates factor XI (part of the intrinsic pathway).
Alternatively, damage to blood vessels leads to release of tissue
factor and activation of factor VII (start of the extrinsic pathway).
The extrinsic and intrinsic pathways merge with activation of factor
X. Activation of factor X by factor IX of the intrinsic pathway
requires factor VIII (antihemophilic factor).
Factor X activates prothrombin to thrombin.
Thrombin removes small fibrinopeptides from fibrinogen to form
fibrin.
Note that the absence of factor VIII is the cause of classic
hemophilia. Factor VIII is encoded on the X chromosome, so the
disease is much more prominent in males, because they have
only one X chromosome.
As wounds heal, clots must be removed. The principal agent for
dissolving clots is an enzyme called plasmin, which is
synthesized as the inactive zymogen called plasminogen.
Plasminogen is activated by a number of proteases, the most
important of which is tissue-type plasminogen activator (t-PA). tPA can be extremely effective in initiating the cascade to dissolve
the unwanted blood clot involved in stroke or heart attack.