Download 3.4 Linear equations and Intercept form

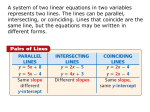
Name________________
AT Algebra
Date_________
3.4 Linear Equations and Int-form
So far in chapter 3 we have looked at linear relationships using recursive routines,
graphs, and tables. Today we are going to learn how to write linear equations.
A linear equation shows a relationship between any two variables(we tend to use x and y
fairly often).
These equations are written in the form
y = b + mx
m represents the _____________________ or _______________________.
b represents the _____________________ or _______________________.
Lets look at a few basic examples:
x
x
y
y
x
y
0
-2
0
10
3
-14
1
1
1
15
4
-20
2
4
2
20
5
-26
3
7
10
60
6
-32
4
10
20
110
7
-42
b=
b=
b=
m=
m=
m=
Now lets come up with a few linear equations that model some real world situations:
Manisha starts her exercise routine by jogging to the gym. Her trainer says this
activity burns 215 calories. Her workout at the gym is to pedal a stationary bike. This
activity burns 3.8 calories per minute.
Pedaling
Total Cal.
time(min)
Burned
Lets fill out the table:
x
y
0
After 20 min, how many calories has she burned?
1
2
20
How long did it take her to burn 443 calories?
30
45
Can you come up with a linear equation to model this
scenario?
60
_________________________
Lets check our equation by:
1) plotting the points from our table in the calculators
2) graphing our equation in the calculators
Equations in the form y = b + mx are said to be in intercept form. Why?
Practice:
1)Write a linear equation to model the situation(make sure to define variables): Sam has
already burned 325 calories before he begins to swim. If he swims he burns 7.8 calories
per minute.
2) A minivan is 220 miles from its destination, Flint. It begins traveling toward Flint at
72 mi/hr.
a) Define variables and write an equation in intercept form of the relationship.(if you
need to use a table).
b) Use the equation to calculate the location of the minivan after 2.5 hours.
c) When will the minivan be 130 miles from Flint?
d) From your equation, what is the real-world meaning of M?
Homework: (you may want to do your work on a separate piece of paper)
1) The equation d = 24 – 45t can be used to model the distance a person is from a
destination while driving down a highway( d= distance in miles, t= time in hours).
a) At what time will the person be 16 miles from their destination?
b) How far has the person traveled after 30 minutes?
c) What is the real world meaning of both the 24 and 45 from the equation?
2) Answer #8a-c on page 184 in your text. (Be careful that your equation works for
every value in the table. Pay attention to the x-values).
a)
b)
c)
3) Write a linear equation in intercept form to represent the info in the tables:
x
y
x
y
0
10
5
7
1
-1
6
9
2
-12
7
11
3
-23
8
13
4
-34
9
15
_______________
_____________________
Bonus: Answer questions #10a-c on p184 in your text.
a)
b)
c)