* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Investigation 3
Survey
Document related concepts
Transcript
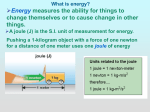
Name________________________________________________________ Date__________________________ Investigation 3 Work, Power, Energy, Impulse, Momentum Work, Power, and Energy In physics, the definition of work is very different from its use in everyday conversation. Specifically, work equals the force acting on an object multiplied by the distance the object moves in the direction of the force. Or in equation form: work = force x distance. 1. Write your mass in kilograms, mass = _________________ kg. (If you know your weight in pounds, you can get an approximate value of your mass by dividing your weight in Pounds by 2.2). 2. When you climb stairs, you are doing work lifting your body upward against the earth’s downward gravitational pull. The force you need to exert to lift yourself vertically at a constant velocity is equal to your weight (remember w = m x g, where g = 10 m/s2). Calculate your weight in Newtons, weight = ____________________ Newtons. Now calculate the work you do in climbing stairs. Remember that the work done is the force (your weight) times the distance you move the object (height of the stairs). Work = Force x (distance moved in the direction of the force) The approximate height of the staircase outside our lab is _________ m. The work done climbing the stairs is _______________ Joules 3. Time yourself climbing the stairs. You can do it rapidly, slowly, or at any speed you choose. But no matter how you do it, hold onto the railing. The time is _____________ seconds 4. Now find your power output while you were climbing the stairs. Power output work done in Joules time in seconds _____________ Joules or Watts sec How does your power output compare to a 100 Watt lightbulb? (rhetorical question) 5. This value can also be expressed in horsepower. In order to do so, divide the power output expressed in Watts by 746 to get your horsepower. ______________ hp How does your power output compare to a horse’s power output? (rhetorical question) Kinetic Energy represents the ability or capacity of an object to do work because of its motion (the energy an object has because of it is moving). The units for kinetic energy are the same as the units for work. In order to determine the kinetic energy of an object, the following expression can be used: kinetic energy = (1/2) x mass x (velocity)2 6. Calculate the kinetic energy of your physics book (mass = 2 kg) when thrown with a velocity of 3 m/s toward a wall. ____________ Joules 7. If you threw the book with a velocity that was twice as great, would the damage to the wall by twice as much? Explain. Potential energy represents the ability or capacity of an object to do work be cause of its position (the energy an object has because of where it is located). The units for potential energy are the same as the units for work. In order to determine the potential energy of an object (specifically, gravitational potential energy), the following expression can be used: potential energy = (mass) x g x (height) = (weight) x (height) 8. Calculate the potential energy of your physics book when held 3 meters above the floor. ____________ Joules 9. You let the book drop. When the book is 1 meter above the floor, calculate its potential energy. ____________ Joules 10. Instead of dropping the book, suppose you threw the book downward with a velocity of 10 m/s from a height of 3 m. Calculate the potential energy of the book when it is 1 meter above the floor. ____________ Joules 11. If you were to double the height from which you dropped the book, would it hit the floor twice as hard? Explain. Conservation of Energy We know that energy cannot be created or destroyed, and we also know that it can be converted from one form to another (e.g., kinetic energy to potential energy and vice versa). So, we say that the total mechanical energy is “conserved” (conservation of energy), i.e., the value of the total mechanical energy stays the same. Suppose a 1 kg ball is at the top of a 40 meter high cliff. In the first case, at position A, we drop the ball and in the second case we throw the ball downward so that it leaves our hand at 10 m/s. Position D is just before the ball hits the ground. Take the acceleration due to gravity to be 10 m/s2. Complete the table below. Make as few calculations as possible. If you keep in mind the idea of conservation of energy, you will not need to make only a few calculations. Notice that the gravitational potential energy is zero at position D, that is, the potential energy is measured from the ground. (Notice that the heights are given, not the time.) A position ball dropped 10 m B gravitational potential energy (Joules) kinetic energy (Joules) ball thrown downward at 10 m/s total mechanical energy (Joules) gravitational potential energy (Joules) kinetic energy (Joules) total mechanical energy (Joules) A 10 m C B C 20 m D 0 0 D ground After the ball hits the ground and stops, its gravitational potential energy is zero, its kinetic energy is zero, and therefore its total mechanical energy appears to be zero. So what happened to all the energy? Impulse and Momentum The Impulse-Momentum relationship says: Impulse = Force x time of impact = change in momentum 1. 2. An unfortunate bug splatters on the windshield of a car traveling at 60 mi/hr on the freeway. a. Compare the force of the car on the bug to the force of the bug on the car. Which one is greater? b. The time of impact is the same for both the bug and the car. Compare the impulse on the bug to the impulse on the car. Which one is greater? c. Compare the change in momentum of the bug to the change in momentum of the car. Which one is greater? d. Does the bug or the car undergo the greater acceleration? Explain briefly. Block A is 8 kg and is sliding on a horizontal, frictionless surface at 4 m/s. It collides with and sticks to a 2 kg block that is at rest. a. What is the value of the total momentum of the system before the collision? b. What should the value of the total momentum of the system be after the collision? c. What are the speeds of the blocks after the collision? A 50 kg bungee jumper jumps off a bridge. She is in free fall for 3 sec. At 3 sec the bungee cord begins to stretch, slows her down, and brings her to a stop 2 sec later. Take the acceleration due to gravity to be 10 m/s2. Fill in the blanks in the following table. type of motion time (sec) velocity (m/s) 0 0 momentum (kg m/s) 1 sec 2 sec 1 free fall 2 3 3 sec slowed by bungee v=0 4 5 0 5 sec By how much did her momentum change from time t = 3 sec to time t = 5 sec? ____________________ kg m/s What is the value of the impulse on her from 3 sec to 5 sec?? ____________________ Newton sec What is the average force that acted on her by the bungee cord from 3 sec to 5 sec? ____________________ Newtons Would there be a problem if the bungee cord stopped her in 1/10 sec instead of 2 sec? Explain. Momentum – Recoil A steel ball (A = 4 kg) and a wooden ball (B = 1 kg) are at rest and separated by a compressed spring. 1. What is the value of the total momentum of the system before the spring is released? The spring is now released causing the balls to recoil in opposite directions. In this case, A 2. what is the value of the total momentum of the system? 3. does the spring exert a greater force on ball A or ball B? 4. which ball has a higher recoil speed? Why? Explain. 5. If you were to jump straight upward from the earth’s surface, will the earth recoil? Explain. B spring Two-dimensinal Elastic Collision 3. The diagram shows the top view of the corner of a pool table with the cue ball and the eight ball. Carefully draw the position of the cue ball when it makes contact with the eight ball so that it causes the eight ball rolls into the corner pocket. Show also the path of the cue ball takes after the collision. cue ball 8