Download Homework Set Solutions Chapter 20

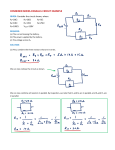
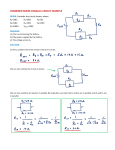
P21 Homework Set #4 Solutions Chapter 23
P23.3. Prepare: Circuits are generally drawn with straight lines and 90  angles for the wires. We also
usually orient the battery with the positive terminal up so the higher potential part of the circuit is toward the top
of the paper.
Solve:
Assess: The elements that are in series with each other have the same current in them; the elements that are in
parallel with each other have the same potential difference across them.
P23.11. Prepare: Please refer to Figure P23.11. The three resistances in (a), (b), and (c) are parallel
resistors. We will thus use Equation 23.12 to find the equivalent resistance.
Solve: (a) The equivalent resistance is
1
 1
1
1 
Req  


  1.0 
 2.0  3.0  6.0  
(b) The equivalent resistance is
1
 1
1
1 
Req  


  1.0 
3.0

3.0

3.0


(c) The equivalent resistance is
1
 1
1
1 
Req  


  0.5 
2.0

1.0

2.0


Assess: We must learn how to combine series and parallel resistors.
P23.15. Prepare: The resistance of the three 60  resistors in parallel is
1
1
 1
1
1   3 
Req  


 
  2 0 
6

0

6

0

6

0
   60  

Solve: That parallel combination in series with the 30  resistor adds to an equivalent resistance of 50 .
So that’s the answer: the three 60  resistors in parallel with each other, and then that combination in series with
the 30  resistor.
Assess: There are typical resistances that one can buy; generally one can’t (cheaply) buy resistors with every
possible value of resistance. So it is common to combine the resistors you have in combinations of series and
parallel to arrive at a different value of equivalent resistance called for in the circuit.
P23.17. Prepare: The connecting wires are ideal with zero resistance. We have to reduce the circuit to a
single equivalent resistor by continuing to identify resistors that are in series or parallel combinations.
Solve:
For the first step, the resistors 30  and 45  are in parallel. Their equivalent resistance is
1
1
1
 Req 1  18 


Req 1 30  45 
For the second step, resistors 42  and Req 1  18  are in series. Therefore,
Req 2  Req 1  42   18   42   60 
For the third step, the resistors 40  and Req 2  60  are in parallel. So,
1
1
1
 Req 3  24 


Req 3 60  40 
The equivalent resistance of the circuit is 24 .
Assess: Have a good understanding of how series and parallel resistors combine to obtain equivalent resistors.
P23.23. Prepare: Please refer to Figure P23.23. Assume that the connecting wire and the battery are ideal. The
middle and right branches are in parallel, so the potential difference across these two branches must be the same.
Solve: The currents in the middle and right branches are known, so the potential differences across the two
branches, using Ohm’s law, are Vmiddle  (3.0 A)R  Vright  (2.0 A)(R + 10 ).
This is easily solved to give R  20 . The middle resistor R is connected directly across the battery, thus (for an
ideal battery, with no internal resistance) the potential difference Vmiddle equals the emf of the battery. That is
E  Vmiddle  (3.0 A)(20 )  60 V.
Assess: Note that the potential difference across parallel resistors is the same.
P23.25. Prepare: Assume ideal batteries and wires and ohmic resistors. Label the top resistor as 1 and the
other three from left to right 2, 3, and 4. The total resistance is
Rtot  50  
5 0 
 6667 
3
Solve: The current through the battery (and R1 ) is then I  V  Rtot  (10 V)  (6667 )  15 A. From the
junction law and symmetry that current splits up evenly in the other three resistors, so I 2  I3  I 4  050 A.
Now V1  I1R1  (15 A)(50 )  75 V. The loop law using the battery,
R1 ,
and
R2
shows that
V2  10 V  75 V  25 V and similarly for V3 and V4 .
R I (A) V (V)
R1 1.5 7.5
R2 0.50 2.5
R3 0.50 2.5
R4 0.50 2.5
Assess: From symmetry we expect the results to be the same for R2 , R3 , and R4 .
P23.27. Prepare: The battery and the connecting wires are ideal. The figure shows how to simplify the circuit
in Figure P23.27 using the laws of series and parallel resistances. We have labeled the resistors as R1  6.0 , R2
 15 , R3  6.0 , and R4  4.0 . Having reduced the circuit to a single equivalent resistance Req, we will
reverse the procedure and “build up” the circuit using the loop law and the junction law to find the current and
potential difference of each resistor.
Solve: R3 and R4 are combined to get R34  10 , and then R34 and R2 are combined to obtain R234:
1
1
1
1
1
 R234  6 




R234 R2 R34 15  10 
Next, R234 and R1 are combined to obtain
Req  R234  R1  6.0   6.0   12 
From the final circuit,
I
E
24 V

 2.0 A
Req 12 
Thus, the current through the battery and R1 is IR1  2.0 A and the potential difference across R1 is I(R1)  (2.0 A)
(6.0 )  12 V.
As we rebuild the circuit, we note that series resistors must have the same current I and that parallel resistors
must have the same potential difference V.
In Step 1 of the previous figure, Req  12  is returned to R1  6.0  and R234  6.0  in series. Both resistors
must have the same 2.0 A current as Req. We then use Ohm’s law to find
VR1  (2 .0A)(6.0 )  12 V
VR234 (2.0 A)(6.0 )  12 V
As a check, 12 V  12 V  24 V, which was V of the Req resistor. In Step 2, the resistance R234 is returned to R2
and R34 in parallel. Both resistors must have the same V  12 V as the resistor R234. Then from Ohm’s law,
I R2 
12 V
 0.8 A
15 
I R34 
12 V
 1.2 A
10 
As a check, IR2  IR34  2.0 A, which was the current I of the R234 resistor. In Step 3, R34 is returned to R3 and R4
in series. Both resistors must have the same 1.2 A as the R34 resistor. We then use Ohm’s law to find
(V)R3  (1.2 A)(6.0 )  7.2 V
(V)R4  (1.2 A)(4.0 )  4.8 V
As a check, 7.2 V  4.8 V 12 V, which was V of the resistor R34.
Resistor
Potential difference (V)
R1
R2
R3
R4
The three steps as we rebuild our circuit are shown.
12
12
7.2
4.8
Current (A)
2.0
0.8
1.2
1.2
Assess: This problem requires a good understanding of how to first reduce a circuit to a single equivalent
resistance and then to build up a circuit.
P23.29. Prepare: The battery and the connecting wires are ideal. The figure shows how to simplify the
circuit in Figure P23.29 using the laws of series and parallel resistances. Having reduced the circuit to a single
equivalent resistance, we will reverse the procedure and “build up” the circuit using the loop law and the junction
law to find the current and potential difference of each resistor.
Solve:
From the last circuit in the diagram,
I
E
12 V

 2.0 A
6.0  6.0 
Thus, the current through the battery is 2.0 A. As we rebuild the circuit, we note that series resistors must have
the same current I and that parallel resistors must have the same potential difference V.
In Step 1, the 6.0  resistor is returned to a 3.0  and 3.0  resistor in series. Both resistors must have the same
2.0 A current as the 6.0  resistance. We then use Ohm’s law to find
V3  (2.0 A)(3.0 )  6.0 V
As a check, 6.0 V  6.0 V  12 V, which was V of the 6.0  resistor. In Step 2, one of the two 3.0  resistances
is returned to the 4.0 , 48 , and 16  resistors in parallel. The three resistors must have the same V  6.0 V.
From Ohm’s law,
6V
6V
6V
I4 
 1.5 A
I 48 
 0.125 A I16 
 0.375 A
4
48 
16 
Resistor
Potential difference (V)
Current (A)
3.0 
6.0
2.0
4.0 
6.0
1.5
48 
6.0
0.13
16 
6.0
0.38
Assess: The larger the resistance, the smaller the current it carries. This is what we would have expected.
P23.37. Prepare: Please refer to Figure P23.37. The following visual overview shows how to find the
equivalent capacitance of the three capacitors shown in the figure.
Solve: Because C1 and C2 are in parallel, their equivalent capacitance Ceq 12 is
Ceq 12  C1  C2  20 F  60 F  80 F
Then, Ceq 12 and C3 are in series. So,
1
1
1
1
1
9
80




 (  F)1  Ceq 
 F  8.9  F
C eq Ceq 12 C3 80  F 10  F 80
9
Assess:
Learn well how to combine series and parallel capacitances.
P23.43. Prepare: Current and voltage during a capacitor discharge are given by Equations 23.22. Because
the charge on a capacitor is Q = CV, the decay of the capacitor charge is given by Q  Q0 et/.
Solve: The time constant is   RC  (1.0  103 )(10  106 F)  0.010 s.
The initial charge on the capacitor is Q0  20 C and it decays to 10 C in time t. That is,
 10  C 
t
10 C  (20 C)et/0.010 s  ln  2  C    0.010 s  t  (0.010 s) ln 2  6.9 ms


Assess: A time constant of a few milliseconds is reasonable.