Download The Sine Function

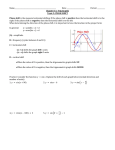
The Sine Function
The sine function f(x) = sin(x) has the following properties
 The domain of the sine function is all the real numbers.
 The period of the function is 2π.
 sin(x) = sin(x + 2π) for all x.
 The function is odd: symmetric with respect to the origin.
This is also stated by saying sin(x) = -sin(-x)
 -1 ≤ sin (x) ≤ 1. This is the range of the sine function.
 The sine function is not one-to-one. For each y-value in the interval [-1, 1] there
are infinitely many x, such that sin (x) = y.
The inverse of sine is arcsine, f(x) = asin (x). It has the following
properties:
 The function is one to one.
 The domain is -1 ≤ x ≤ 1.
 The range is –π / 2 ≤ asin (x) ≤ π / 2
 If x is in the interval –π / 2 ≤ x ≤ π / 2, then: if sin (x) = y then
asin (y) = x.
When solving sin (x) = k, where k is any real number in the interval [0, 2π)
 if |k| > 1, there are no solutions.
 if |k| = 1, there is one solution.
 if |k| < 1, there are two solutions.
The question is how do you find the solutions without using a graphing calculator to
approximate the solutions using the Calc button? We look at the problem with four cases
k = -1, 1, -1 < k < 0, and 0 ≤ k < 1.
Case 1: sin (x) = -1.
1. Taking the inverse of both sides: x = asin (-1) = -π / 2.
2. Since x = -π / 2 is not in the interval [0, 2π) we add 2π to our answer and get
x = 3π / 2.
Case 2: sin (x) = 1.
1. Taking the inverse of both sides: x = asin (1) = π / 2. This
is the answer.
Case 3: sin (x) = k where -1 < k < 0.
1. For this problem there are two answers. An example of
the problem is shown to the right. The points where the
two graphs intersect are the solutions.
2. To find one of the solutions we calculate asin(k). Since k
is negative this will give us a value that is less than 0.
3. Add 2π to this number. This will give one solution as x =
asin(k) + 2π. This solution is the intersection point on the right.
4. The other solution is at π - asin(k).
Case 4: sin(x) = k where 0 < k < 1
1. The first solution is at x = asin(k).
2. The second solution is at x = π – asin (k).
Notice that case 3 and case 4 are almost the same except that we
had to add 2 π to the one solution of case 3.
Finding All Solutions to sin (x) = k
So once you have found the solutions in the interval [0, 2π) how
do you get all solutions that solve sin (x) = k. Let us suppose that you found that sin(x) =
k in the interval [0, 2π) had two solutions called x1 and x2. Every other solution is a
multiple of 2π from one of these solutions. That is, all the solutions are:
x = x1 + 2n π
x = x2 + 2n π where n is any integer.
A more general form of sine
A more general form of the sine function is f(x) = A sin(ax – b)
 A is the amplitude. If you were to measure the vertical
displacement from the highest point of the graph to the
lowest point of the graph you would find that this distance
is |2A|. In the graph to the right A = 5. We usually express
the amplitude as a positive number even though A may be
negative.
 a determines the period. To find the period p: p = 2π / |a|.
For the graph to the right the period is p = π / 2.
 a and b are used to find what is called the phase shift. To find the phase shift for
the problem to the right:
o Inside the sine function is the linear expression 4x – 3
o Factor out the 4.
o 4x – 3 = 4(x – ¾).
o The phase shift is ¾. The phase shift determines how much the sine
function is shifted left or right. Suppose b is positive:
 The expression sin [a(x – b)] is shifted b units to the right.
 The expression sin [a(x + b)] is shifted b units to the left.
Solving Asin (ax – b) = k
1. Divide by A and you get: sin (ax – b) = k / A.
2. Use the method on page 1 above to find the solutions to sin (x) = k / A. Call these
solutions x1 and x2.
3. Solve ax – b = x1 and ax – b = x2. You obtain x = (x1+b)/a, and x = (x2+b)/a.
These are the two solutions in one complete period of A sin(ax – b) = k.
4. Notice that the period is 2π / a.
5. All solutions are found by:
x = (x1+b)/a + 2nπ / a
x = (x2+b)/a + 2nπ / a where n is any integer