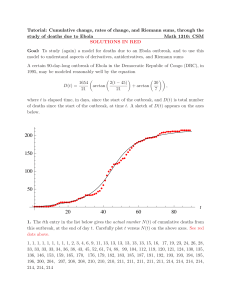
SOLUTIONS TO PROBLEM SET 4 1. Without loss of generality
... generator of X, then the function g defined by g(x) = f (|x|) should belong to the infinitesimal generator of B. On the other hand, g is C20 (R) if and only if f is C20 (R+ ) with f 0 (0) = 0. Thus, the domain of the generator are twice continuously differentiable functions on [0, ∞) with zero deriv ...
... generator of X, then the function g defined by g(x) = f (|x|) should belong to the infinitesimal generator of B. On the other hand, g is C20 (R) if and only if f is C20 (R+ ) with f 0 (0) = 0. Thus, the domain of the generator are twice continuously differentiable functions on [0, ∞) with zero deriv ...
Academy Algebra II 5.7: Apply the Fundamental Theorem of Algebra
... Fundamental Theorem of Algebra • If f(x) is a polynomial with degree of n (where n>0), then the equation f(x) = 0 has at least one solution. • Corollary: The equation f(x) = 0 has exactly n solutions provided each solution repeated twice is counted as 2 solutions, each solution repeated three times ...
... Fundamental Theorem of Algebra • If f(x) is a polynomial with degree of n (where n>0), then the equation f(x) = 0 has at least one solution. • Corollary: The equation f(x) = 0 has exactly n solutions provided each solution repeated twice is counted as 2 solutions, each solution repeated three times ...
20 40 60 80 t 50 100 150 200
... of Calculus) is this. Suppose a quantity D(t) has a constant rate of change R over some interval. Then total change in D(t) over the interval = rate of change R over the interval ⇥ length of interval (for example: if your speed is a constant 60 mph for an interval of length 1 sec = 1/3600 of an hour ...
... of Calculus) is this. Suppose a quantity D(t) has a constant rate of change R over some interval. Then total change in D(t) over the interval = rate of change R over the interval ⇥ length of interval (for example: if your speed is a constant 60 mph for an interval of length 1 sec = 1/3600 of an hour ...
Math 131The Fundamental Theorem of Calculus (Part 2)
... Suppose we know that the velocity of an object traveling along a line (think car on a straight highway) is given by a continuous function v(t), where t represents time on the interval [ a, b]. How might we determine the net distance the object has travelled? Well, we know that if the velocity were c ...
... Suppose we know that the velocity of an object traveling along a line (think car on a straight highway) is given by a continuous function v(t), where t represents time on the interval [ a, b]. How might we determine the net distance the object has travelled? Well, we know that if the velocity were c ...
Course Code
... Equations: Elimination Methods Determinants: Evaluate 2x2 and 3x3 determinants, Using Cramer’s Rule to solve equations, Find the market equilibrium using Cramer’s Rule, Use Cramer’s Rule for the IncomeDetermination Model Matrices and Determinants, Systems of Linear Equations The Definite Integral: T ...
... Equations: Elimination Methods Determinants: Evaluate 2x2 and 3x3 determinants, Using Cramer’s Rule to solve equations, Find the market equilibrium using Cramer’s Rule, Use Cramer’s Rule for the IncomeDetermination Model Matrices and Determinants, Systems of Linear Equations The Definite Integral: T ...
AP Calculus AB
... Steps for Solving Differential Equations: “Find a solution (or solve) the separable differentiable equation…” 1. Separate the variables 2. Integrate each side 3. Make sure to put C on side with independent variable (normally x) 4. Plug in initial condition and solve for C (if given) 5. Solve for the ...
... Steps for Solving Differential Equations: “Find a solution (or solve) the separable differentiable equation…” 1. Separate the variables 2. Integrate each side 3. Make sure to put C on side with independent variable (normally x) 4. Plug in initial condition and solve for C (if given) 5. Solve for the ...
Fundamental theorem of calculus
The fundamental theorem of calculus is a theorem that links the concept of the derivative of a function with the concept of the function's integral.The first part of the theorem, sometimes called the first fundamental theorem of calculus, is that the definite integration of a function is related to its antiderivative, and can be reversed by differentiation. This part of the theorem is also important because it guarantees the existence of antiderivatives for continuous functions.The second part of the theorem, sometimes called the second fundamental theorem of calculus, is that the definite integral of a function can be computed by using any one of its infinitely-many antiderivatives. This part of the theorem has key practical applications because it markedly simplifies the computation of definite integrals.