
Discrete Symmetries and Gravity G W Gibbons DAMTP
... Racah and the Wigner approach to discrete symmetries for fermions. The Racah approach is basically to use linear (in fact Cliffordian) representions which are complex linear. On the another hand Wigner (followed by almost all textbooks) used what he called co-representations which contain anti-linea ...
... Racah and the Wigner approach to discrete symmetries for fermions. The Racah approach is basically to use linear (in fact Cliffordian) representions which are complex linear. On the another hand Wigner (followed by almost all textbooks) used what he called co-representations which contain anti-linea ...
Persistent currents controlled by non-classical electromagnetic fields J. D
... quasi 1D rings with an even number of coherent electrons. The result for diamagnetic currents can be obtained if one replaces ϕe by ϕe + ϕ0/2 [1]. For quantum electromagnetic fields, the electric and magnetic fields are the well-known dual quantum variables [6]. One can also associate them, by simpl ...
... quasi 1D rings with an even number of coherent electrons. The result for diamagnetic currents can be obtained if one replaces ϕe by ϕe + ϕ0/2 [1]. For quantum electromagnetic fields, the electric and magnetic fields are the well-known dual quantum variables [6]. One can also associate them, by simpl ...
notes
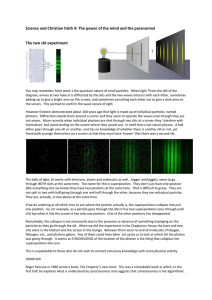
... adding up to give a bright area on the screen, and sometimes cancelling each other out to give a dark area on the screen. This seemed to confirm the wave nature of light. However Einstein demonstrated about 100 years ago that light is made up of individual particles, named photons. Diffractions bend ...
... adding up to give a bright area on the screen, and sometimes cancelling each other out to give a dark area on the screen. This seemed to confirm the wave nature of light. However Einstein demonstrated about 100 years ago that light is made up of individual particles, named photons. Diffractions bend ...
Orthogonal Polynomials 1 Introduction 2 Orthogonal Polynomials
... If a particle's position is described by coordinates (x y z ), then its momentum in the x direction is given by the operator ...
... If a particle's position is described by coordinates (x y z ), then its momentum in the x direction is given by the operator ...
WHAT IS NOETHER`S THEOREM? - Ohio State Department of
... Exercise 4. If the Lagrangian does not depend on time, use a similar argument to show that H = ∂ẋi Lẋi − L is conserved. Remember that just because the Lagrangian function does not depend on time, the total Lagrangian might because it depends on x and ẋ. What is the common name for H? 3. Why Do W ...
... Exercise 4. If the Lagrangian does not depend on time, use a similar argument to show that H = ∂ẋi Lẋi − L is conserved. Remember that just because the Lagrangian function does not depend on time, the total Lagrangian might because it depends on x and ẋ. What is the common name for H? 3. Why Do W ...
The Nature of Light - What are Photons
... As strange as it may seem, the physical world, as we observe it, can be much more simply and elegantly understood using a quite different set of assumptions: 1. The most fundamental constructs in physics are the electromagnetic and gravitational interactions of matter. 2. Time enters these fundament ...
... As strange as it may seem, the physical world, as we observe it, can be much more simply and elegantly understood using a quite different set of assumptions: 1. The most fundamental constructs in physics are the electromagnetic and gravitational interactions of matter. 2. Time enters these fundament ...
Constructing mehod of 2-EPP with different quantum error correcting
... The proposed protocol using G(1) and G(2) is performed as follows: • Alice measures c′1 , · · · , c′l on her own quantum states and obtains a measurement outcome aC ′ = (ac′1 , · · · , ac′l ). • Bob measures c′1 , · · · , c′l on his own quantum states and obtains a measurement outcome bC ′ = (bc′1 , ...
... The proposed protocol using G(1) and G(2) is performed as follows: • Alice measures c′1 , · · · , c′l on her own quantum states and obtains a measurement outcome aC ′ = (ac′1 , · · · , ac′l ). • Bob measures c′1 , · · · , c′l on his own quantum states and obtains a measurement outcome bC ′ = (bc′1 , ...
Chapter 8 - Bakersfield College
... D. The metastable atoms, as they return to their ground states, create photons all of the same frequency and all of whose waves are coherent or exactly in step. 8-12. Quantum Mechanics A. The theory of quantum mechanics was developed by Erwin Schrödinger, Werner Heisenberg, and others during the mid ...
... D. The metastable atoms, as they return to their ground states, create photons all of the same frequency and all of whose waves are coherent or exactly in step. 8-12. Quantum Mechanics A. The theory of quantum mechanics was developed by Erwin Schrödinger, Werner Heisenberg, and others during the mid ...
Complete Introduction
... enough, although the correction does indeed satisfy that condition by insertion of the necessary reciprocal factorial of particle number, it is not itself quite correct. The functions S(p) appearing in Eq. (3) of the correction unfortunately are not uniquely defined. One easily sees, for example, th ...
... enough, although the correction does indeed satisfy that condition by insertion of the necessary reciprocal factorial of particle number, it is not itself quite correct. The functions S(p) appearing in Eq. (3) of the correction unfortunately are not uniquely defined. One easily sees, for example, th ...
LOW ENERGY NUCLEAR FUSION REACTIONS: QUANTUM
... Recently in this series of papers {1 - 10} the ECE fermion equation has been used to give an explanation of low energy nuclear reaction (LENR { 11} ), which has been observed experimentally to be reproducible and repeatable, and which has been developed into a new source of energy. In this paper the ...
... Recently in this series of papers {1 - 10} the ECE fermion equation has been used to give an explanation of low energy nuclear reaction (LENR { 11} ), which has been observed experimentally to be reproducible and repeatable, and which has been developed into a new source of energy. In this paper the ...
Interpretive Themes in Quantum Physics: Curriculum Development and Outcomes
... Student interest in quantum mechanics at CU before instruction in modern physics is moderately high, at an average between 75-80% favorable. [FIG. 2] However, their post-instruction interest typically decreases (to below 70%), with negative responses increasing significantly (p < 0.001) – nearly 1/3 ...
... Student interest in quantum mechanics at CU before instruction in modern physics is moderately high, at an average between 75-80% favorable. [FIG. 2] However, their post-instruction interest typically decreases (to below 70%), with negative responses increasing significantly (p < 0.001) – nearly 1/3 ...
May 2009
... M09Q.3 - Pion-Atom Scattering (J94Q.3) Problem Consider the following 1-dimensional version of inelastic scattering of a projectile off an atom. In the 1-d case one speaks of transmission-reflection coefficients rather than differential scattering cross sections. Our 1-d atom consists of an “electro ...
... M09Q.3 - Pion-Atom Scattering (J94Q.3) Problem Consider the following 1-dimensional version of inelastic scattering of a projectile off an atom. In the 1-d case one speaks of transmission-reflection coefficients rather than differential scattering cross sections. Our 1-d atom consists of an “electro ...
pdf - at www.arxiv.org.
... the disturbance vanishingly small. Famously, this is not the case in quantum mechanics; as I will try to show here in a simple but dramatical example. What happens exactly when we perform a measurement on a quantum system is still an open question, but one thing is clear: it is not at all like the c ...
... the disturbance vanishingly small. Famously, this is not the case in quantum mechanics; as I will try to show here in a simple but dramatical example. What happens exactly when we perform a measurement on a quantum system is still an open question, but one thing is clear: it is not at all like the c ...
Lieb-Robinson bounds and the speed of light from topological order
... The cosmological horizon problem.— The isotropy of the cosmic microwave background presents us with the horizon problem: how is it possible that regions that were never causally connected have the same temperature? The horizon problem arises from the stipulation that interactions cannot travel faste ...
... The cosmological horizon problem.— The isotropy of the cosmic microwave background presents us with the horizon problem: how is it possible that regions that were never causally connected have the same temperature? The horizon problem arises from the stipulation that interactions cannot travel faste ...
Quantum computers - start [kondor.etf.rs]
... • The example gives an answer to the question asked before – why state of the system has to be specified with complex amplitudes and cannot be specified with probabilities only Dušan Gajević ...
... • The example gives an answer to the question asked before – why state of the system has to be specified with complex amplitudes and cannot be specified with probabilities only Dušan Gajević ...
Physics 13: Introduction to Modern Physics Tufts University, Fall 2008
... By “modern physics” we often mean the new understanding of the world that developed over the last century and has at its foundation relativity and quantum physics. This course will cover a variety of topics spanning Einstein’s annus mirabilis of 1905 to more contemporary topics such as observational ...
... By “modern physics” we often mean the new understanding of the world that developed over the last century and has at its foundation relativity and quantum physics. This course will cover a variety of topics spanning Einstein’s annus mirabilis of 1905 to more contemporary topics such as observational ...














![Quantum computers - start [kondor.etf.rs]](http://s1.studyres.com/store/data/008623556_1-6dce2335493dbd35f44ebeba6fa8564e-300x300.png)







