The Quantum Mechanical Model
... Erwin Schrodinger (mathematical equations using probability, quantum numbers) ...
... Erwin Schrodinger (mathematical equations using probability, quantum numbers) ...
What is Light?
... •If is fundamentally impossible to make simultaneous measurements of position and velocity with infinite accuracy •I.e. The measurement procedure itself limits the accuracy to which we can determine the position and velocity simultaneously ...
... •If is fundamentally impossible to make simultaneous measurements of position and velocity with infinite accuracy •I.e. The measurement procedure itself limits the accuracy to which we can determine the position and velocity simultaneously ...
PH1012 - Physics 1B
... The two first level modules in physics provide a balanced introduction to university physics, assuming a prior knowledge of mathematics and physics that corresponds to Higher grade passes in these subjects. The modules include appropriate coverage of the traditional disciplines of classical physics, ...
... The two first level modules in physics provide a balanced introduction to university physics, assuming a prior knowledge of mathematics and physics that corresponds to Higher grade passes in these subjects. The modules include appropriate coverage of the traditional disciplines of classical physics, ...
Electric Fields and Capacitors Solutions
... Indicate the direction of a force on a positive test “charge”; their density indicates the strength of this force. They are useful for describing the effect of any non-contact force. 3. Electric field lines are drawn (a) from positive charges to negative charges 4. How is intensity indicated in a fi ...
... Indicate the direction of a force on a positive test “charge”; their density indicates the strength of this force. They are useful for describing the effect of any non-contact force. 3. Electric field lines are drawn (a) from positive charges to negative charges 4. How is intensity indicated in a fi ...
Answers to Coursebook questions – Chapter J1
... electrons occupying that state be differentiated in some way. The inner shell has no quantum numbers other than energy, and so the only quantum number that can separate two electrons is the spin. One electron can have spin up and the other spin down. So we can have at most two electrons. In the othe ...
... electrons occupying that state be differentiated in some way. The inner shell has no quantum numbers other than energy, and so the only quantum number that can separate two electrons is the spin. One electron can have spin up and the other spin down. So we can have at most two electrons. In the othe ...
Quantum computing with nanoscale infrastructure
... Bottom in which he pointed to the possibility of manipulating the quantum behaviour of single atoms. This is exactly what is done today, fifty years later, in ion trap quantum ‘computers’. In ion traps, a few research groups in the world are able to collect chains of 8-10 ionised atoms. Each of thes ...
... Bottom in which he pointed to the possibility of manipulating the quantum behaviour of single atoms. This is exactly what is done today, fifty years later, in ion trap quantum ‘computers’. In ion traps, a few research groups in the world are able to collect chains of 8-10 ionised atoms. Each of thes ...
Document
... Operation”, IEEE Transactions on Electron Devices, Volume 52, Issue 2, Feb. 2005 Page(s):227 – 236. ...
... Operation”, IEEE Transactions on Electron Devices, Volume 52, Issue 2, Feb. 2005 Page(s):227 – 236. ...
M.Sc._Physics_Sem_II.pdf
... 1-D Harmonic Oscillator: treatment of 1D harmonic oscillator problem with use of operator and matrix formalism. Transformations, conservation laws and Symmetries: Translation in space and conservation of linear momentum, translation in time and conservation of energy, rotation in space, quantum gene ...
... 1-D Harmonic Oscillator: treatment of 1D harmonic oscillator problem with use of operator and matrix formalism. Transformations, conservation laws and Symmetries: Translation in space and conservation of linear momentum, translation in time and conservation of energy, rotation in space, quantum gene ...
Chapter 7 (Lecture 10) Hydrogen Atom The explanation of
... operates in ordinary space only; operates only in spin space. All components of satisfy the same commutation relations. Thus satisfies the same commutation relations as ...
... operates in ordinary space only; operates only in spin space. All components of satisfy the same commutation relations. Thus satisfies the same commutation relations as ...
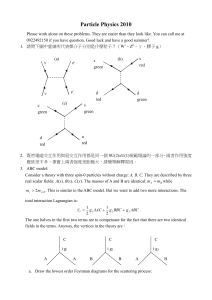
Particle Physics
... of a Klein-Gordon Field. The second and third term could be considered as the negative of the potential. Since the Lagrangian is composed only of the inner products of 3 vectors, it is invariant under O(3), ie. the 3D rotation. The Hamiltonian can be written as ...
... of a Klein-Gordon Field. The second and third term could be considered as the negative of the potential. Since the Lagrangian is composed only of the inner products of 3 vectors, it is invariant under O(3), ie. the 3D rotation. The Hamiltonian can be written as ...
Synonyms Definition Theoretical Background
... Since the inner product called the probability amplitude xi | z is a scalar, the state vector is a linear combination, or superposition, of the basis states. The act of measurement results in the normalized projection of the state vector onto the corresponding subspace. For example, performing ...
... Since the inner product called the probability amplitude xi | z is a scalar, the state vector is a linear combination, or superposition, of the basis states. The act of measurement results in the normalized projection of the state vector onto the corresponding subspace. For example, performing ...
Quantum Nonlocality
... What each bulb does next is determined by the present states of two other bulb in the array. The system is started at some random state of illumination and allowed to evolve. The array will soon “self-organize” into a very orderly set of behaviors, cycling through a very limited set of patterns ...
... What each bulb does next is determined by the present states of two other bulb in the array. The system is started at some random state of illumination and allowed to evolve. The array will soon “self-organize” into a very orderly set of behaviors, cycling through a very limited set of patterns ...
The relation between the ( hypothetical) intrinsic vibrational motion
... number of Φ0= hc/e, otherwise the wavefunction will not be kept singlevalued. Such point is discussed in detail for a particle in confined motion in the book by Frenkel[8], and in its simpler form this results in the BohrSommerfeld-Wilson quantization rules. Although no special attention was given t ...
... number of Φ0= hc/e, otherwise the wavefunction will not be kept singlevalued. Such point is discussed in detail for a particle in confined motion in the book by Frenkel[8], and in its simpler form this results in the BohrSommerfeld-Wilson quantization rules. Although no special attention was given t ...
... polarimeter: We have found a, variation of +1/&& of the detection efficiencies when rotating the polarimeters. This spurious effect has been explained as small displacements of the light beam The effect of impinging onto the photocathode. these variations on the quantum mechanical predictions has be ...
The concepts of an atom and chemical bond in physics and chemistry
... ∆ρ(r) = 0. Thus the molecular structure becomes known as well. There are four different types of critical points, but the most important for this particular analysis is the so called bond critical point (BCP), which indicates the existence of a chemical bond between given atoms. In general, every su ...
... ∆ρ(r) = 0. Thus the molecular structure becomes known as well. There are four different types of critical points, but the most important for this particular analysis is the so called bond critical point (BCP), which indicates the existence of a chemical bond between given atoms. In general, every su ...
PDF
... of quantum state spaces (viz. Alfsen and Schultz, 2003 [?]) cannot be overestimated. Moreover, the introduction of non-commutative C*-algebras in noncommutative geometry has already played important roles in expanding the Hilbert space perspective of quantum mechanics developed by von Neumann. Furth ...
... of quantum state spaces (viz. Alfsen and Schultz, 2003 [?]) cannot be overestimated. Moreover, the introduction of non-commutative C*-algebras in noncommutative geometry has already played important roles in expanding the Hilbert space perspective of quantum mechanics developed by von Neumann. Furth ...