The quantum system - Università degli Studi dell`Insubria
... which form the vector operator p$ p$x , p$y . Both components of the linear momentum operator commute with the Hamiltonian [ H$, p$x ] [ H$, p$y ] 0 and then we find again that the linear momentum is a constant of motion. This mathematical result has again a deep physical significance: the lin ...
... which form the vector operator p$ p$x , p$y . Both components of the linear momentum operator commute with the Hamiltonian [ H$, p$x ] [ H$, p$y ] 0 and then we find again that the linear momentum is a constant of motion. This mathematical result has again a deep physical significance: the lin ...
Magnetoresistance.
... orbital angular momentum. Orbital angular momentum is the qunatum number that changes in the quantum Hall effect. When polycrystalline samples (or arbitrary angles of the applied magnetic field to the atomic planes) are used in the Hall experiment it is necessary for electrons to cross from one atom ...
... orbital angular momentum. Orbital angular momentum is the qunatum number that changes in the quantum Hall effect. When polycrystalline samples (or arbitrary angles of the applied magnetic field to the atomic planes) are used in the Hall experiment it is necessary for electrons to cross from one atom ...
Spin-current and other unusual phases in magnetized triangular lattice antiferromagnets
... been proposed that the plateaus are Wigner crystals of triplets [14–16]. There exists a spin model which is derived from the Shastry-Sutherland Hamiltonian [17] for which the plateaus are demonstrated to originate from such ordered states. However, in this model there are plateaus at 1#4, 1#2, and 3 ...
... been proposed that the plateaus are Wigner crystals of triplets [14–16]. There exists a spin model which is derived from the Shastry-Sutherland Hamiltonian [17] for which the plateaus are demonstrated to originate from such ordered states. However, in this model there are plateaus at 1#4, 1#2, and 3 ...
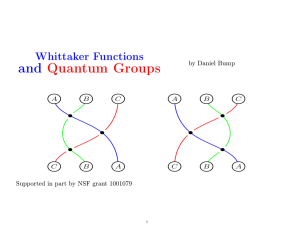
Whittaker Functions and Quantum Groups
... of vertices that there exists a vertex ST such that the Yang-Baxter equation is true in the sense that the following two partition functions are equal: ...
... of vertices that there exists a vertex ST such that the Yang-Baxter equation is true in the sense that the following two partition functions are equal: ...
Frustrated Quantum Magnetism with Laser-Dressed Rydberg Atoms
... Rb atoms and choose |g+ i ≡ |52 S1/2 , F = 2, mF = 2i and |g- i ≡ |52 S1/2 , F = 1, mF = 1i as our spin-1/2 [see Fig. 1(b)]. Interactions between these effective spin states are induced by admixing highly lying Rydberg states to the atomic ground states with laser light, where van der Waals (vdW) in ...
... Rb atoms and choose |g+ i ≡ |52 S1/2 , F = 2, mF = 2i and |g- i ≡ |52 S1/2 , F = 1, mF = 1i as our spin-1/2 [see Fig. 1(b)]. Interactions between these effective spin states are induced by admixing highly lying Rydberg states to the atomic ground states with laser light, where van der Waals (vdW) in ...
PDF
... in three different “states”: it can be bound to its system, unbound, or in the ground state (the state such that information contained in the carrier is not relevant anymore.) Carriers become unbound when a measurement is made on their associated systems. They are then free to interact with other sy ...
... in three different “states”: it can be bound to its system, unbound, or in the ground state (the state such that information contained in the carrier is not relevant anymore.) Carriers become unbound when a measurement is made on their associated systems. They are then free to interact with other sy ...
Detailing Coherent, Minimum Uncertainty States of Gravitons, as
... author is convinced after trial and error that the standard which should be used is that of talking of information, in the Shannon sense, for entropy, and to find ways to make a relationship between quantum computing operations, and Shannon information. Making the identification of entropy as being ...
... author is convinced after trial and error that the standard which should be used is that of talking of information, in the Shannon sense, for entropy, and to find ways to make a relationship between quantum computing operations, and Shannon information. Making the identification of entropy as being ...
PDF
... experiment can be used to eliminate the modulus π uncertainty. Specifically, if one applies a dc magnetic field parallel to the RF field, it leads to a new oscillation (in the population of either level) at the fundamental frequency, with exactly the same phase as that of the driving field. In the e ...
... experiment can be used to eliminate the modulus π uncertainty. Specifically, if one applies a dc magnetic field parallel to the RF field, it leads to a new oscillation (in the population of either level) at the fundamental frequency, with exactly the same phase as that of the driving field. In the e ...
Spontaneous Symmetry Breaking in Non Abelian Gauge Theories
... We can take a similar Lagrangian for the scalar field as above L = |∂φ|2 − V (|φ|2 ) (where Lorentz and SU (N ) index sums are implied) which has the required invariance. To promote the symmetry to a local symmetry, we must replace the derivatives with covariant derivatives Dµ = ∂µ − igAµ . The gaug ...
... We can take a similar Lagrangian for the scalar field as above L = |∂φ|2 − V (|φ|2 ) (where Lorentz and SU (N ) index sums are implied) which has the required invariance. To promote the symmetry to a local symmetry, we must replace the derivatives with covariant derivatives Dµ = ∂µ − igAµ . The gaug ...
TQFTs - UCSB Math Department
... Bordism here is called a smooth manifold triad. A cobordism from Y1 to Y2 there is defined as a 5-tuple (X; ∂1 X, ∂2 X; h1 , h2 ), where (X; ∂1 X, ∂2 X) is a smooth triad and hi : ∂i X → Yi , i = 1, 2 are diffeomorphisms. This definition leads to a category of manifolds, which are often called the co ...
... Bordism here is called a smooth manifold triad. A cobordism from Y1 to Y2 there is defined as a 5-tuple (X; ∂1 X, ∂2 X; h1 , h2 ), where (X; ∂1 X, ∂2 X) is a smooth triad and hi : ∂i X → Yi , i = 1, 2 are diffeomorphisms. This definition leads to a category of manifolds, which are often called the co ...
Radiative cascade of highly excited hydrogen atoms in strong magnetic... Türker Topçu and Francis Robicheaux 兲
... Formation of highly excited antihydrogen atoms have been reported by two experimental groups where cold antiprotons are merged with a cold trapped positron plasma at roughly 关1兴 16 K and 关2,3兴 4 K in magnetic fields of about 3 and 5.4 T, respectively. The goal is to perform Lorentz and CPT violation ...
... Formation of highly excited antihydrogen atoms have been reported by two experimental groups where cold antiprotons are merged with a cold trapped positron plasma at roughly 关1兴 16 K and 关2,3兴 4 K in magnetic fields of about 3 and 5.4 T, respectively. The goal is to perform Lorentz and CPT violation ...
Curriculum Vitae Irinel Chiorescu
... direction I developed at FSU is focusing on quantum coherence and it involves studies of spin dynamics in diluted spin systems and molecular magnets. The research program benefited from an Alfred P. Sloan Research Fellowship and a NSF Career award, now continued with a regular NSF grant. This goal i ...
... direction I developed at FSU is focusing on quantum coherence and it involves studies of spin dynamics in diluted spin systems and molecular magnets. The research program benefited from an Alfred P. Sloan Research Fellowship and a NSF Career award, now continued with a regular NSF grant. This goal i ...
10 Supersymmetric gauge dynamics: N = 1 10.1 Confinement and
... If confinement occurs, we would expect a linear potential between the two quarks. Indeed, in an unconfined theory, the electric flux is uniformly distributed over a sphere surrounding a charge, and falls-o↵ as 1/r2 . In a confining theory with flux tubes, the flux tube has a fixed cross-sectional ar ...
... If confinement occurs, we would expect a linear potential between the two quarks. Indeed, in an unconfined theory, the electric flux is uniformly distributed over a sphere surrounding a charge, and falls-o↵ as 1/r2 . In a confining theory with flux tubes, the flux tube has a fixed cross-sectional ar ...




![[tex110] Occupation number fluctuations](http://s1.studyres.com/store/data/004846223_1-cb4dd2663e349dfb101f2bc5cbb873e7-300x300.png)