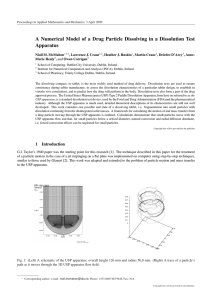
Langevin Equation
... Here γ u (with γ = µ−1 ) is the systematic part of the molecular force, and F (t) is the random component with hF i = 0. (We could also include a nonstochastic external force, but will not do so here.) We also assume there is no causal connection of F (t) with the velocity, i.e. F (t) is uncorrelate ...
... Here γ u (with γ = µ−1 ) is the systematic part of the molecular force, and F (t) is the random component with hF i = 0. (We could also include a nonstochastic external force, but will not do so here.) We also assume there is no causal connection of F (t) with the velocity, i.e. F (t) is uncorrelate ...
Why Probability?
... Maintains sample of weighted particles Each particle is a single realization of all non-evidence nodes Particle is weighted by likelihood of observation given particle Particles are resampled with probability proportional to weight ...
... Maintains sample of weighted particles Each particle is a single realization of all non-evidence nodes Particle is weighted by likelihood of observation given particle Particles are resampled with probability proportional to weight ...
Markov Chain Monte Carlo (MCMC)
... population has a chance (greater than zero) of being selected in the sample, and this probability can be accurately determined Nonprobability sampling is any sampling method where some elements of the population have no chance of selection does not allow to estimate sampling errors! Replacement of ...
... population has a chance (greater than zero) of being selected in the sample, and this probability can be accurately determined Nonprobability sampling is any sampling method where some elements of the population have no chance of selection does not allow to estimate sampling errors! Replacement of ...
May - Uniservity CLC
... Particles A and B, of mass 2m and m respectively, are attached to the ends of a light inextensible string. The string passes over a small smooth pulley fixed at the edge of a rough horizontal table. Particle A is held on the table, while B rests on a smooth plane inclined at 30 to the horizontal, a ...
... Particles A and B, of mass 2m and m respectively, are attached to the ends of a light inextensible string. The string passes over a small smooth pulley fixed at the edge of a rough horizontal table. Particle A is held on the table, while B rests on a smooth plane inclined at 30 to the horizontal, a ...
Seventh lecture, 18.11.03 (Tunneling times and introduction to weak
... Very rare events may be very strange as well. Ritchie, Story, & Hulet 1991 ...
... Very rare events may be very strange as well. Ritchie, Story, & Hulet 1991 ...
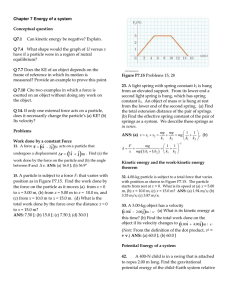
Chapter 7 Energy of a system Conceptual question Q7.1 Can kinetic
... as only Batman knows how, eventually getting it to swing enough that he can reach a ledge when the rope makes a 60.0° angle with the vertical. How much work was done by the gravitational force on Batman in this ...
... as only Batman knows how, eventually getting it to swing enough that he can reach a ledge when the rope makes a 60.0° angle with the vertical. How much work was done by the gravitational force on Batman in this ...
Chapter 7 Energy of a system Conceptual question Q7.1 Can kinetic
... 19. If it takes 4.00 J of work to stretch a Hooke'slaw spring 10.0 cm from its unstressed length, determine the extra work required to stretch it an additional 10.0 cm. ANS: 12.0 J. 3.Batman, whose mass is 80.0 kg, is dangling on the free end of a 12.0-m rope, the other end of which is fixed to a tr ...
... 19. If it takes 4.00 J of work to stretch a Hooke'slaw spring 10.0 cm from its unstressed length, determine the extra work required to stretch it an additional 10.0 cm. ANS: 12.0 J. 3.Batman, whose mass is 80.0 kg, is dangling on the free end of a 12.0-m rope, the other end of which is fixed to a tr ...
Filtering Actions of Few Probabilistic Effects
... • Elements of our representation: State variables, world states Prior graphical model (e.g., Bayes Net) Transition function for deterministic actions Probability distribution for probabilistic actions Represents distribution over deterministic outcomes of probabilistic actions given curr ...
... • Elements of our representation: State variables, world states Prior graphical model (e.g., Bayes Net) Transition function for deterministic actions Probability distribution for probabilistic actions Represents distribution over deterministic outcomes of probabilistic actions given curr ...