S2 Poisson Distribution
... For a Poisson distribution to be valid, the mean and variance need to be equal or very close. In this situation they are not close and so a Poisson distribution would not be a likely model. ...
... For a Poisson distribution to be valid, the mean and variance need to be equal or very close. In this situation they are not close and so a Poisson distribution would not be a likely model. ...
Gaussian Probability Distribution
... The Gaussian distribution can be derived from the binomial (or Poisson) assuming: u p is finite u N is very large u we have a continuous variable rather than a discrete variable An example illustrating the small difference between the two distributions under the above conditions: u Consider tossing ...
... The Gaussian distribution can be derived from the binomial (or Poisson) assuming: u p is finite u N is very large u we have a continuous variable rather than a discrete variable An example illustrating the small difference between the two distributions under the above conditions: u Consider tossing ...
The Binomial Distribution
... Defn: A random variable is a variable whose values are determined by chance. We will denote a random variable by a capital letter, such as X, and denote particular values of the variable by the corresponding lower case letter, x. Thus we read P(X = x) as: “the probability that the random variable X ...
... Defn: A random variable is a variable whose values are determined by chance. We will denote a random variable by a capital letter, such as X, and denote particular values of the variable by the corresponding lower case letter, x. Thus we read P(X = x) as: “the probability that the random variable X ...
Gan/Kass Phys 416 LAB 3
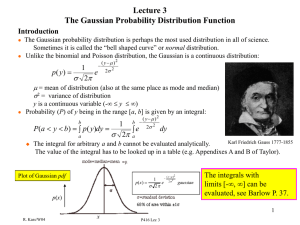
... "A random variable is any rule that associates a number with each outcome in S". b) If y is described by a Gaussian distribution with mean µ = 0 and variance σ2 = 1 then the probability that a < y < b is: 1 b − (1/2) y 2 P(a < y < b) = dy ∫e 2π a c) The C.L.T. is still true even if the Yi 's are fro ...
... "A random variable is any rule that associates a number with each outcome in S". b) If y is described by a Gaussian distribution with mean µ = 0 and variance σ2 = 1 then the probability that a < y < b is: 1 b − (1/2) y 2 P(a < y < b) = dy ∫e 2π a c) The C.L.T. is still true even if the Yi 's are fro ...
Chapter 13. Binomial Distributions
... Chapter 13. Binomial Distributions The Binomial Setting and Binomial Distributions Note. The binomial setting consists of an experiment with observations satisfying: 1. There are a fixed number n of observations. 2. The n observations are all independent. That is, knowing the result of one observati ...
... Chapter 13. Binomial Distributions The Binomial Setting and Binomial Distributions Note. The binomial setting consists of an experiment with observations satisfying: 1. There are a fixed number n of observations. 2. The n observations are all independent. That is, knowing the result of one observati ...
Binomial Theorem
... Triangle". To make the triangle, you start with a pyramid of three 1's, like this: Then you get the next row of numbers by adding the pairs of numbers from above. (Where there is only one number above, you just carry down the 1.) ...
... Triangle". To make the triangle, you start with a pyramid of three 1's, like this: Then you get the next row of numbers by adding the pairs of numbers from above. (Where there is only one number above, you just carry down the 1.) ...
Practice Exam 2 solutions
... favorite cereal. The four different prizes are randomly put into the boxes at the factory. If his mom decides to buy the cereal until all four prizes are obtained, then what is the expected number of boxes she will have to buy until the boy has obtained all four prizes? Solution: We can think of thi ...
... favorite cereal. The four different prizes are randomly put into the boxes at the factory. If his mom decides to buy the cereal until all four prizes are obtained, then what is the expected number of boxes she will have to buy until the boy has obtained all four prizes? Solution: We can think of thi ...
ACTSSOLHW8
... 8. Solution: Let X be the number of tourists that show up. Note that X is Binomial(θ = .98, n = 21). The event that a seat is not available occurs if and only if X = 21, and P (X = 21) = (.98)21 = .6543. The expected loss of the operator due to overbooking is (0)P (X < 21) + (100)P (X = 21) = (100) ...
... 8. Solution: Let X be the number of tourists that show up. Note that X is Binomial(θ = .98, n = 21). The event that a seat is not available occurs if and only if X = 21, and P (X = 21) = (.98)21 = .6543. The expected loss of the operator due to overbooking is (0)P (X < 21) + (100)P (X = 21) = (100) ...
Pascal`s triangle
... Also note that the integer number in each circle in Figure 2 (e.g. the number “3” in the case denoted by the star) is the sum of the numbers in the “parent” circles (in this case, 1 + 2 = 3): that is because the number of ways to get to a circle of interest (from the top of the tree) with a sequenc ...
... Also note that the integer number in each circle in Figure 2 (e.g. the number “3” in the case denoted by the star) is the sum of the numbers in the “parent” circles (in this case, 1 + 2 = 3): that is because the number of ways to get to a circle of interest (from the top of the tree) with a sequenc ...
n - UTK-EECS
... Repeat the same random experiment n times. (Experiments are independent of each other) ...
... Repeat the same random experiment n times. (Experiments are independent of each other) ...
Chapter 5.2: Mean, Variance, and Standard Deviation
... Recall that the mean for a sample or population was computed by adding the values and dividing by the total number of values ...
... Recall that the mean for a sample or population was computed by adding the values and dividing by the total number of values ...
Pascal*s Triangle and Binomial Theorem
... • (1) REMEMBER – This is a PDF problem because it computes the exact probability for one outcome or value • In the calculator: 2nd VARS -> binompdf -> Enter the following: (sample size, probability, number of successes or failures • In this example it will look like this: binompdf(30,.5,12) = .08 = ...
... • (1) REMEMBER – This is a PDF problem because it computes the exact probability for one outcome or value • In the calculator: 2nd VARS -> binompdf -> Enter the following: (sample size, probability, number of successes or failures • In this example it will look like this: binompdf(30,.5,12) = .08 = ...
simulations, sampling distributions, probability and random variables
... B = thesecond die shows a 6, and C = the sum of the numbers showing is 3. By making a table of the 36 possible outcomes of rolling two six-sided dice, you will find that P(A) = 1/6, P(B) = 1/6, and P(C) = 2/36. Events A and B are independent. Suppose you are told that the sum of the numbers sho ...
... B = thesecond die shows a 6, and C = the sum of the numbers showing is 3. By making a table of the 36 possible outcomes of rolling two six-sided dice, you will find that P(A) = 1/6, P(B) = 1/6, and P(C) = 2/36. Events A and B are independent. Suppose you are told that the sum of the numbers sho ...
Hints on PROBABILITY probability_hints
... B = thesecond die shows a 6, and C = the sum of the numbers showing is 3. By making a table of the 36 possible outcomes of rolling two six-sided dice, you will find that P(A) = 1/6, P(B) = 1/6, and P(C) = 2/36. Events A and B are independent. Suppose you are told that the sum of the numbers sho ...
... B = thesecond die shows a 6, and C = the sum of the numbers showing is 3. By making a table of the 36 possible outcomes of rolling two six-sided dice, you will find that P(A) = 1/6, P(B) = 1/6, and P(C) = 2/36. Events A and B are independent. Suppose you are told that the sum of the numbers sho ...
Chapter 8 - jonesmth110
... The same experiment is repeated several times (a fixed number of times). There are only two possible outcomes: ...
... The same experiment is repeated several times (a fixed number of times). There are only two possible outcomes: ...
maesp 102 probability and random
... b) A man either drives a car or catches a train to go to office each day. He never goes 2 days in a raw by train but if he drives one day, then the next day he is just as likely to drive again as he is to travel by train . Now suppose that on the first day of the week, the man tossed a fair dice and ...
... b) A man either drives a car or catches a train to go to office each day. He never goes 2 days in a raw by train but if he drives one day, then the next day he is just as likely to drive again as he is to travel by train . Now suppose that on the first day of the week, the man tossed a fair dice and ...