Handout on Empirical Distribution Function
... of observed values of random variables that are iid or ‘independent identically distributed’, i.e., are independent random variables all of which follow the same probability law summarized by the distribution function FX (t) = F (t) = P (X1 ≤ t) Recall that a distribution function is a nondecreasing ...
... of observed values of random variables that are iid or ‘independent identically distributed’, i.e., are independent random variables all of which follow the same probability law summarized by the distribution function FX (t) = F (t) = P (X1 ≤ t) Recall that a distribution function is a nondecreasing ...
Events A1,...An are said to be mutually independent if for all subsets
... Suppose in a collection of people there are some number with height 6’, and equal numbers with heights 5’11” and 6’1”. The mean or average of this distribution is 6’, as can be determined by summing the heights of all the people and dividing by the number of people, or equivalently by summing over d ...
... Suppose in a collection of people there are some number with height 6’, and equal numbers with heights 5’11” and 6’1”. The mean or average of this distribution is 6’, as can be determined by summing the heights of all the people and dividing by the number of people, or equivalently by summing over d ...
Reteaching - Gulfport School District
... Step 1 The power of the binomial corresponds to the second number in each row of Pascal’s Triangle. Because the power of this binomial is 5, use the row of Pascal’s Triangle with 5 as the second number. The numbers of this row are the coefficients of the expansion. Step 2 The exponents of the x-term ...
... Step 1 The power of the binomial corresponds to the second number in each row of Pascal’s Triangle. Because the power of this binomial is 5, use the row of Pascal’s Triangle with 5 as the second number. The numbers of this row are the coefficients of the expansion. Step 2 The exponents of the x-term ...
1.2 Interpretations 1.3 Distributions
... this is non-standard notation and won’t be used in these notes. (4) If A and B are sets, A ∪ B is the union of A and B. It is the set of elements which are either in A or B. As a set A ∪ B = {x | x ∈ A or x ∈ B}. (5) If A ⊂ B then Ac is the complement to A (in B). It is the set of elements of B whic ...
... this is non-standard notation and won’t be used in these notes. (4) If A and B are sets, A ∪ B is the union of A and B. It is the set of elements which are either in A or B. As a set A ∪ B = {x | x ∈ A or x ∈ B}. (5) If A ⊂ B then Ac is the complement to A (in B). It is the set of elements of B whic ...
- Catalyst
... given a normal distribution with µ = 13 and σ = 4? Answer: 0.204 What is the probability that –1000 ≤ x ≤ 1000 given a normal distribution with µ = 13 and σ = 4? Answer: 1.000 ...
... given a normal distribution with µ = 13 and σ = 4? Answer: 0.204 What is the probability that –1000 ≤ x ≤ 1000 given a normal distribution with µ = 13 and σ = 4? Answer: 1.000 ...
LAB1
... left scatterings. There are 14 rows of staggered pins. This is the n in the C.L.T. equation. Each scattering contributes a deviation, Yn, from the center horizontal location where the ball is released. The deviation can have positive or negative sign and its value depends on the particular angle of ...
... left scatterings. There are 14 rows of staggered pins. This is the n in the C.L.T. equation. Each scattering contributes a deviation, Yn, from the center horizontal location where the ball is released. The deviation can have positive or negative sign and its value depends on the particular angle of ...
Probability PowerPoint
... P(tail) = 1/2 Since there are only two outcomes, you have 50/50 chance to get a head or a tail. ...
... P(tail) = 1/2 Since there are only two outcomes, you have 50/50 chance to get a head or a tail. ...
PPT
... Probability of any specific sequence Number of possible sequences with the given elements ...
... Probability of any specific sequence Number of possible sequences with the given elements ...
PPT
... •If X and Y are two random variables we obtain: E(g(X,Y))= {all (x,y)} g(x,y)P(X=x, Y=y). This allows to prove that E[X+Y] = E[X] + E[Y]: E(X) = {all (x,y)} x P(X=x, Y=y); E(Y) = {all (x,y)} y P(X=x, Y=y); E(X+Y) = {all (x,y)} (x+y) P(X=x, Y=y); E(X+Y) = E(X) + E (Y) ...
... •If X and Y are two random variables we obtain: E(g(X,Y))= {all (x,y)} g(x,y)P(X=x, Y=y). This allows to prove that E[X+Y] = E[X] + E[Y]: E(X) = {all (x,y)} x P(X=x, Y=y); E(Y) = {all (x,y)} y P(X=x, Y=y); E(X+Y) = {all (x,y)} (x+y) P(X=x, Y=y); E(X+Y) = E(X) + E (Y) ...
Lecture08
... vi) Note the progression of the bars for each number of successes k. For k=0, 3, 4, 5 successes, the probability increases as n increases. For k=1,2 successes, the probability decreases as n increases. But in every case the difference between the bars for n=100 and n=1000 is tiny. There appears to b ...
... vi) Note the progression of the bars for each number of successes k. For k=0, 3, 4, 5 successes, the probability increases as n increases. For k=1,2 successes, the probability decreases as n increases. But in every case the difference between the bars for n=100 and n=1000 is tiny. There appears to b ...
2006/07 late summer resit paper - Queen Mary University of London
... the event “the student passes the first exam”, B be the event “the student passes the second exam”, and and H be the event “the student is hard-working”. Suppose that P(A) = 2/3, P(B) = 3/4, P(A ∩ B) = 7/12, and P(H) = 1/2. a) Express the following events in words and find their probabilities: i) A ...
... the event “the student passes the first exam”, B be the event “the student passes the second exam”, and and H be the event “the student is hard-working”. Suppose that P(A) = 2/3, P(B) = 3/4, P(A ∩ B) = 7/12, and P(H) = 1/2. a) Express the following events in words and find their probabilities: i) A ...
Gaussian Probability Distribution
... “A random variable is any rule that associates a number with each outcome in S” (Devore, in “probability and Statistics for Engineering and the Sciences”). Here S is the set of possible outcomes. l Recall if y is described by a Gaussian pdf with mean () of zero and =1 then the probability that a
... “A random variable is any rule that associates a number with each outcome in S” (Devore, in “probability and Statistics for Engineering and the Sciences”). Here S is the set of possible outcomes. l Recall if y is described by a Gaussian pdf with mean () of zero and =1 then the probability that a
Gaussian Probability Distribution
... “A random variable is any rule that associates a number with each outcome in S” (Devore, in “probability and Statistics for Engineering and the Sciences”). Here S is the set of possible outcomes. l Recall if y is described by a Gaussian pdf with mean () of zero and =1 then the probability that a
... “A random variable is any rule that associates a number with each outcome in S” (Devore, in “probability and Statistics for Engineering and the Sciences”). Here S is the set of possible outcomes. l Recall if y is described by a Gaussian pdf with mean () of zero and =1 then the probability that a
Gaussian Probability Distribution
... The Gaussian distribution can be derived from the binomial (or Poisson) assuming: u p is finite u N is very large u we have a continuous variable rather than a discrete variable l An example illustrating the small difference between the two distributions under the above conditions: u Consider tossin ...
... The Gaussian distribution can be derived from the binomial (or Poisson) assuming: u p is finite u N is very large u we have a continuous variable rather than a discrete variable l An example illustrating the small difference between the two distributions under the above conditions: u Consider tossin ...
MTH/STA 561 EXPONENTIAL PROBABILITY DISTRIBUTION As
... that is, F (y) = e y/ for any positive rational number y. By the right continuity of F (y), it follows that F (y) = e y/ for any positive real number y. Therefore, Y has an exponential distribution with parameter > 0. The reason that the geometric and exponential distribution should both have the me ...
... that is, F (y) = e y/ for any positive rational number y. By the right continuity of F (y), it follows that F (y) = e y/ for any positive real number y. Therefore, Y has an exponential distribution with parameter > 0. The reason that the geometric and exponential distribution should both have the me ...
Solution - Statistics
... Here, E[N√] = 120 × 0.1 = 12 and V ar(N ) = E[N ] = 12. So, E[W ] = 12 × 4 = 48 pounds, sd(W ) = 12 × 4 + 12 × 42 = 15.5 pounds. 2. A light bulb has a lifetime that is exponential with a mean of µ = 200 days. When it burns out, a janitor replaces it immediately. In addition, there is a handyman who ...
... Here, E[N√] = 120 × 0.1 = 12 and V ar(N ) = E[N ] = 12. So, E[W ] = 12 × 4 = 48 pounds, sd(W ) = 12 × 4 + 12 × 42 = 15.5 pounds. 2. A light bulb has a lifetime that is exponential with a mean of µ = 200 days. When it burns out, a janitor replaces it immediately. In addition, there is a handyman who ...
Probability—the description of random events
... distribution of outcomes. This distribution will approach an asymptotic form as the number of events increases. 1. If the distribution is represented as the number of occurrences of each outcome, the distribution is called the frequency distribution function. 2. If the distribution is represented as ...
... distribution of outcomes. This distribution will approach an asymptotic form as the number of events increases. 1. If the distribution is represented as the number of occurrences of each outcome, the distribution is called the frequency distribution function. 2. If the distribution is represented as ...
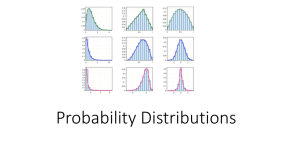
Probability Distributions - Sys
... Many of the pharmaceuticals on the market today were found using high throughput screening assays. In these assays, large numbers of random molecules are tested and of these only a few show appreciable activity. If we assume that the success rate in these screens is one in ten thousand (p=0.0001), t ...
... Many of the pharmaceuticals on the market today were found using high throughput screening assays. In these assays, large numbers of random molecules are tested and of these only a few show appreciable activity. If we assume that the success rate in these screens is one in ten thousand (p=0.0001), t ...