MATH 342
... To measure angles with a protractor, put the small hole of the protractor on the vertex of the angle and the horizontal line of the protractor on one of the rays of the angle, then the angle measurement is indicated by the position of the other ray, using the numbers greater than 90 degrees if the a ...
... To measure angles with a protractor, put the small hole of the protractor on the vertex of the angle and the horizontal line of the protractor on one of the rays of the angle, then the angle measurement is indicated by the position of the other ray, using the numbers greater than 90 degrees if the a ...
Review Sheet from AHighSchool
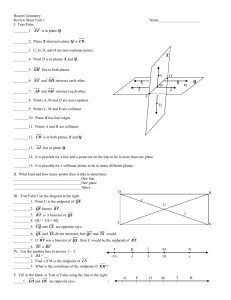
... If 2 lines intersect, then they intersect in exactly one point. Two intersecting lines are always contained in exactly one plane. Three non-collinear points can lie in each of 2 different planes. Horizontal planes will never intersect. ...
... If 2 lines intersect, then they intersect in exactly one point. Two intersecting lines are always contained in exactly one plane. Three non-collinear points can lie in each of 2 different planes. Horizontal planes will never intersect. ...
An Elementary Introduction to the Hopf Fibration
... a vector and one real number to give the angle. This is far fewer than the nine entries of a 3 × 3 orthogonal matrix we learn to use in linear algebra. In fact, we can cut the number of parameters needed to specify a rotation from four to three, for example, by giving an axis vector whose length det ...
... a vector and one real number to give the angle. This is far fewer than the nine entries of a 3 × 3 orthogonal matrix we learn to use in linear algebra. In fact, we can cut the number of parameters needed to specify a rotation from four to three, for example, by giving an axis vector whose length det ...
5.2 Notes - West Ada
... create a mirror image. Does not change the size or shape but often changes the orientation. Reflect over the x-axis – swap the sign of the y-coordinate Reflect over the y-axis – swap the sign of the x-coordinate ...
... create a mirror image. Does not change the size or shape but often changes the orientation. Reflect over the x-axis – swap the sign of the y-coordinate Reflect over the y-axis – swap the sign of the x-coordinate ...
Stereonets
... Solving geometerical problems – displays geometry and orientation os lines and planes. It is a three-dimensional protractor. With a normal protractor, we can plot trend of lines, measure angles between lines, construct normal e.g., perpendicular lines) line, and rotate lines by specified angles. Ste ...
... Solving geometerical problems – displays geometry and orientation os lines and planes. It is a three-dimensional protractor. With a normal protractor, we can plot trend of lines, measure angles between lines, construct normal e.g., perpendicular lines) line, and rotate lines by specified angles. Ste ...
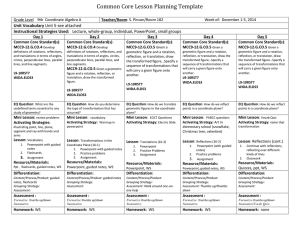
3-6-17 math - Trousdale County Schools
... plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not. 4. Develop definitions of rotations, reflections, an ...
... plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not. 4. Develop definitions of rotations, reflections, an ...