List of Hilbert`s axioms
... One of the things David Hilbert was famous for was giving a modern axiomatization of (Euclidean) (3-dimensional) geometry. Here are his axioms (it is interesting to compare these with Euclid’s axioms): Undefined primitives: point, line, plane Primitive relations: betweenness, containment, congruence ...
... One of the things David Hilbert was famous for was giving a modern axiomatization of (Euclidean) (3-dimensional) geometry. Here are his axioms (it is interesting to compare these with Euclid’s axioms): Undefined primitives: point, line, plane Primitive relations: betweenness, containment, congruence ...
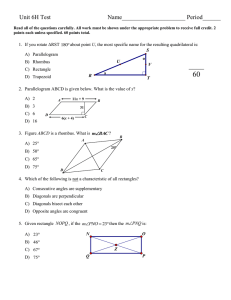
Geometry Fall Final Review
... 9) Name a pair of vertical angles. 10) If the complement of an angle measures 22°, what is the measure of its supplement? 11) Two vertical angles are also complementary. Find the measure of one of the two vertical angles. 12) Two angles form a linear pair. One angle measures (10x – 63). The other a ...
... 9) Name a pair of vertical angles. 10) If the complement of an angle measures 22°, what is the measure of its supplement? 11) Two vertical angles are also complementary. Find the measure of one of the two vertical angles. 12) Two angles form a linear pair. One angle measures (10x – 63). The other a ...
F1.8GD1 Notes on Vectors A vector v is an ordered triple v = (x, y, z
... Then u, v are said to be orthogonal, or at right angles if θ = π/2, ie if u · v = 0. The three basic vectors i, j, k are all mutually orthogonal: i · j = i · k = j · k = 0. Theorem (The triangle inequality) |u + v| ≤ |u| + |v|. Proof. |u + v|2 = (u + v) · (u + v) = |u|2 + 2|u||v| cos(θ) + |v|2 ≤ (|u ...
... Then u, v are said to be orthogonal, or at right angles if θ = π/2, ie if u · v = 0. The three basic vectors i, j, k are all mutually orthogonal: i · j = i · k = j · k = 0. Theorem (The triangle inequality) |u + v| ≤ |u| + |v|. Proof. |u + v|2 = (u + v) · (u + v) = |u|2 + 2|u||v| cos(θ) + |v|2 ≤ (|u ...
Solution
... Hence if we know 3 points both before and after transformation, we will have 6 equations in 6 unknowns and thus in two dimensions if we know how a triangle is transformed we can determine the affine transformation. ...
... Hence if we know 3 points both before and after transformation, we will have 6 equations in 6 unknowns and thus in two dimensions if we know how a triangle is transformed we can determine the affine transformation. ...
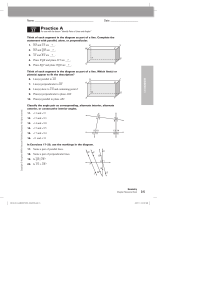
Lecture 1 (L1): Angles and Angle Measures Textbook Section: 4.1
... Angles are measured by the amount of _____________________ from initial to terminal side. When measuring angles on the coordinate plane it is convenient to imagine the angle sitting inside of a _______________________ because if you rotate an angle in the coordinate plane completely around its verte ...
... Angles are measured by the amount of _____________________ from initial to terminal side. When measuring angles on the coordinate plane it is convenient to imagine the angle sitting inside of a _______________________ because if you rotate an angle in the coordinate plane completely around its verte ...