Theory of Computation
... Example. one example of an infinite language can be the constructed by allows Σ = {a, b, c}. Our language L then consists of all 1, 2, 3, 4.... letter words, and this generates an infinite number of words even though the length of the words has to remain finite. This is denoted Σ∗ . We can also talk ...
... Example. one example of an infinite language can be the constructed by allows Σ = {a, b, c}. Our language L then consists of all 1, 2, 3, 4.... letter words, and this generates an infinite number of words even though the length of the words has to remain finite. This is denoted Σ∗ . We can also talk ...
Incompleteness - the UNC Department of Computer Science
... theory. In 1977, Kirby, Paris and Harrington proved that a statement in combinatorics, a version of the Ramsey theorem, is undecidable in the axiomatization of arithmetic given by the Peano axioms but can be proven to be true in the larger system of set theory. Kruskal's tree theorem, which has appl ...
... theory. In 1977, Kirby, Paris and Harrington proved that a statement in combinatorics, a version of the Ramsey theorem, is undecidable in the axiomatization of arithmetic given by the Peano axioms but can be proven to be true in the larger system of set theory. Kruskal's tree theorem, which has appl ...
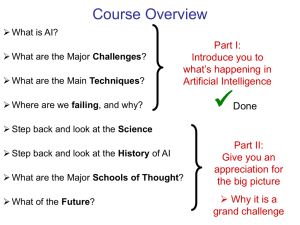
Step back and look at the Science
... Won a Prize in 1936 for work on probability theory Became interested in Hilbert’s Entscheidungsproblem (decision problem) of 1928 1936, Turing came up with proof of impossibility …but Alonzo Church published independent paper also showing that it is impossible 1937 Turing’s "On computable ...
... Won a Prize in 1936 for work on probability theory Became interested in Hilbert’s Entscheidungsproblem (decision problem) of 1928 1936, Turing came up with proof of impossibility …but Alonzo Church published independent paper also showing that it is impossible 1937 Turing’s "On computable ...
Humans, Computer, and Computational Complexity
... proof is a syntactical object that exists within a formal axiomatic system, but truth is a semantic notion. The technical details are difficult however the key ideas within the proof demonstrate the power of paradox in showing the limits of formal mathematics. The key example to consider is the sta ...
... proof is a syntactical object that exists within a formal axiomatic system, but truth is a semantic notion. The technical details are difficult however the key ideas within the proof demonstrate the power of paradox in showing the limits of formal mathematics. The key example to consider is the sta ...
Two-sample-test
... the same net volume, whether or not this volume is 16.0 ounces. In the past, the customers would complain their quality if the weight difference is larger than 0.25 ounces. And the variances for these two machines are assumed to be the same σ1=σ2=0.12. This problem could become a two-sample-t-test o ...
... the same net volume, whether or not this volume is 16.0 ounces. In the past, the customers would complain their quality if the weight difference is larger than 0.25 ounces. And the variances for these two machines are assumed to be the same σ1=σ2=0.12. This problem could become a two-sample-t-test o ...
on Computability
... rules, can be computed by one of TM. Consistent • Briefly, a Turing machine can be thought of as a black box, which performs a calculation of some kind on an input number. If the calculation reaches a conclusion, or halts then an output number is returned. • One of the consequences of Turing's theor ...
... rules, can be computed by one of TM. Consistent • Briefly, a Turing machine can be thought of as a black box, which performs a calculation of some kind on an input number. If the calculation reaches a conclusion, or halts then an output number is returned. • One of the consequences of Turing's theor ...
5.8.2 Unsolvable Problems
... previously not to exist. Thus, MC cannot exist. We consider two cases, the first in which B∗ is in not C and the second in which it is in C. In the first case, let L be a language in C. In the second, let L be a language in RE − C. Since C is a proper subset of RE and not empty, there is always a la ...
... previously not to exist. Thus, MC cannot exist. We consider two cases, the first in which B∗ is in not C and the second in which it is in C. In the first case, let L be a language in C. In the second, let L be a language in RE − C. Since C is a proper subset of RE and not empty, there is always a la ...
Extended Analog Computer and Turing machines - Hektor
... time. These are, for example, the Analog Recurrent Neural Network [2] and the machines of Blum-Shub-Smale [3]. The second case are models of computation on real numbers and in continuous time. In this scope the important model is the General Purpose Analog Computer proposed by Shannon in 1941. This ...
... time. These are, for example, the Analog Recurrent Neural Network [2] and the machines of Blum-Shub-Smale [3]. The second case are models of computation on real numbers and in continuous time. In this scope the important model is the General Purpose Analog Computer proposed by Shannon in 1941. This ...
Approaching P=NP: Can Soap Bubbles Solve The Steiner Tree
... • Two classes of problems, P and NP – P: Problems that can be solved in time polynomial to the size of the input by a deterministic Turing machine. – NP: Problems that can be solved in time polynomial to the size of the input by a nondeterministic Turing machine. ...
... • Two classes of problems, P and NP – P: Problems that can be solved in time polynomial to the size of the input by a deterministic Turing machine. – NP: Problems that can be solved in time polynomial to the size of the input by a nondeterministic Turing machine. ...
23-24-TuringMachinesHandout
... Random Access Turing Machines A random access Turing machine has: a fixed number of registers a finite length program, composed of instructions with operators such as read, write, load, store, add, sub, jump a tape a program counter Theorem: Standard Turing machines and random access Turing ...
... Random Access Turing Machines A random access Turing machine has: a fixed number of registers a finite length program, composed of instructions with operators such as read, write, load, store, add, sub, jump a tape a program counter Theorem: Standard Turing machines and random access Turing ...
Slides
... Deciding whether a string is in a context-free language can be determined in polynomial time Deciding whether a language is empty is decidable ...
... Deciding whether a string is in a context-free language can be determined in polynomial time Deciding whether a language is empty is decidable ...
7 - blacksacademy.net
... Let M1, M2, ... , Mn , ... be a denumerable list of Turing machines. Two machines are said to behave in the same way towards a number x, if their outputs for x are the same. Two machines are said to be similar if they behave in the same way for every number x. Let U be called a universal machine, de ...
... Let M1, M2, ... , Mn , ... be a denumerable list of Turing machines. Two machines are said to behave in the same way towards a number x, if their outputs for x are the same. Two machines are said to be similar if they behave in the same way for every number x. Let U be called a universal machine, de ...
ppt
... – Hardware need not be fixed to solve any problem. Given a simple hardware design, one can program that hardware to accomplish any task ...
... – Hardware need not be fixed to solve any problem. Given a simple hardware design, one can program that hardware to accomplish any task ...
slides - Center for Collective Dynamics of Complex Systems (CoCo)
... Example of proof in HB system • Proving A∨A→A: Replace B in basic axiom I-(1) by A A→(A→A) Replace B in basic axiom I-(2) by A (A→(A→A))→(A→A) Apply inference rule to the above two formulae A→A Replace B and C in basic axiom III-(3) by A (A→A)→((A→A)→(A∨A→A)) Apply inference rule to the above two f ...
... Example of proof in HB system • Proving A∨A→A: Replace B in basic axiom I-(1) by A A→(A→A) Replace B in basic axiom I-(2) by A (A→(A→A))→(A→A) Apply inference rule to the above two formulae A→A Replace B and C in basic axiom III-(3) by A (A→A)→((A→A)→(A∨A→A)) Apply inference rule to the above two f ...
1996TuringIntro
... a considerable body of evidence, much of it garnered from his own research, that indicates the ways in which human cognitive processing actually operates; on the other, he points to a number of computer programs, again some of them his own, that have succeeded in operating “intelligently” in strikin ...
... a considerable body of evidence, much of it garnered from his own research, that indicates the ways in which human cognitive processing actually operates; on the other, he points to a number of computer programs, again some of them his own, that have succeeded in operating “intelligently” in strikin ...
L11 - Computing at Northumbria University
... • Very informally : anything one model can do any other model can do. – All TOMs have equivalent computational power. ...
... • Very informally : anything one model can do any other model can do. – All TOMs have equivalent computational power. ...