Random Variables. Probability Distributions
... • The random variable X=Sum of the two numbers fair dice turn up is discrete and has the possible values 2 (=1+1), 3,4,…, 12 (=6+6). • There are 6*6=36 equally likely outcomes (1,1), (1,2), …, (6,6), where the first number is that shown on the first die and th second number tat on the other die. • E ...
... • The random variable X=Sum of the two numbers fair dice turn up is discrete and has the possible values 2 (=1+1), 3,4,…, 12 (=6+6). • There are 6*6=36 equally likely outcomes (1,1), (1,2), …, (6,6), where the first number is that shown on the first die and th second number tat on the other die. • E ...
wwtbam
... A complete cycle of a traffic light takes 80 seconds. During each cycle, the light is green for 40 seconds, amber for 10 seconds, and red for 30 seconds. At a randomly chosen time, what is the probability that the light will not be red? ...
... A complete cycle of a traffic light takes 80 seconds. During each cycle, the light is green for 40 seconds, amber for 10 seconds, and red for 30 seconds. At a randomly chosen time, what is the probability that the light will not be red? ...
Understanding Variables - TN-5thGrade
... What is the difference of these two values? ______ 2. What is the value of each of these words? a. variable ______ b. machine ______ c. algebra ______ d. mathematics ______ 3. Find three different words whose values are each equal to 25. Record the words below. ...
... What is the difference of these two values? ______ 2. What is the value of each of these words? a. variable ______ b. machine ______ c. algebra ______ d. mathematics ______ 3. Find three different words whose values are each equal to 25. Record the words below. ...
Georgia Lottery Learning Task PDF
... Expected value is the most likely value of a random variable. In the case of an investment decision, it is the average value of all possible payoffs. In order to find the expected value of a variable, you must first multiply each possible payoff by its probability of occurring, followed by adding al ...
... Expected value is the most likely value of a random variable. In the case of an investment decision, it is the average value of all possible payoffs. In order to find the expected value of a variable, you must first multiply each possible payoff by its probability of occurring, followed by adding al ...
21-325 (Fall 2008): Homework 5 (TWO side) Due by
... Show that X1 + X2 + · · · + Xr has a negative Binomial distribution when the Xi , i = 1, 2, · · · , r are independent and they have the same Geometric distribution with parameter p. Solution. The negative Binomial random variable with parameters (r, p) describes the distribution of the number of tri ...
... Show that X1 + X2 + · · · + Xr has a negative Binomial distribution when the Xi , i = 1, 2, · · · , r are independent and they have the same Geometric distribution with parameter p. Solution. The negative Binomial random variable with parameters (r, p) describes the distribution of the number of tri ...
maesp 102 probability and random
... b) If the random variable X takes the values 1,2,3 and 4 such that 2P(X=1)=3P(X=2)=P(X=3)=5P(X=4) find the probability distribution and cumulative distribution function of X. ...
... b) If the random variable X takes the values 1,2,3 and 4 such that 2P(X=1)=3P(X=2)=P(X=3)=5P(X=4) find the probability distribution and cumulative distribution function of X. ...
HW_1 _AMS_570 1.5 Approximately one
... 1.41 As in example 1.3.6, consider telegraph signals “dot” and “dash” sent in the proportion 3:4, where erratic transmissions cause a dot to become a dash with probability and a dash to become a dot with probability . (a) If a dash is received, what is the probability that a dash has been sent? (b) ...
... 1.41 As in example 1.3.6, consider telegraph signals “dot” and “dash” sent in the proportion 3:4, where erratic transmissions cause a dot to become a dash with probability and a dash to become a dot with probability . (a) If a dash is received, what is the probability that a dash has been sent? (b) ...
Guided Reading page 341 – 344
... A discrete random variable X takes a ________________________________________________ __________________________________________. The probability distribution of a discrete random variable X lists the ____________ and their ___________________________. Value of X ...
... A discrete random variable X takes a ________________________________________________ __________________________________________. The probability distribution of a discrete random variable X lists the ____________ and their ___________________________. Value of X ...
Continuous probability
... For example, the probability that T would be between 2 and 3 minutes would be Pr{ 2 T 3 } = e-2/2 - e-3/2 0.145. It turns out the countable additivity property (1.11) holds when probabilities are given by integrals of the form (1.14). This can be used to find the probability of sets which are ...
... For example, the probability that T would be between 2 and 3 minutes would be Pr{ 2 T 3 } = e-2/2 - e-3/2 0.145. It turns out the countable additivity property (1.11) holds when probabilities are given by integrals of the form (1.14). This can be used to find the probability of sets which are ...
65% are numbered 1 35% are numbered 2 A random sample of 3
... 65% are numbered 1 35% are numbered 2 A random sample of 3 balls is taken from the bag. Find the sampling distribution for the range of the numbers on the 3 selected balls. ...
... 65% are numbered 1 35% are numbered 2 A random sample of 3 balls is taken from the bag. Find the sampling distribution for the range of the numbers on the 3 selected balls. ...
Assignment 2
... 2. Write a computer program that, when given a probability mass function { p j , j 1, 2,..., n} as an input, gives as an output the value of a random variable having this mass function. 3. Give an efficient algorithm to simulate the value of a random variable X such that P( X 1) 0.3 , P( X 2 ...
... 2. Write a computer program that, when given a probability mass function { p j , j 1, 2,..., n} as an input, gives as an output the value of a random variable having this mass function. 3. Give an efficient algorithm to simulate the value of a random variable X such that P( X 1) 0.3 , P( X 2 ...
Markov, Chebyshev, and the Weak Law of Large Numbers
... Markov, Chebyshev, and the Weak Law of Large Numbers The Law of Large Numbers is one of the fundamental theorems of statistics. One version of this theorem, The Weak Law of Large Numbers, can be proven in a fairly straightforward manner using Chebyshev's Theorem, which is, in turn, a special case of ...
... Markov, Chebyshev, and the Weak Law of Large Numbers The Law of Large Numbers is one of the fundamental theorems of statistics. One version of this theorem, The Weak Law of Large Numbers, can be proven in a fairly straightforward manner using Chebyshev's Theorem, which is, in turn, a special case of ...
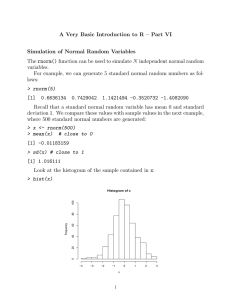
Simulation of Normal Random Numbers
... We can estimate the probability that a normal random variable Y is less than a given value, x: P (Y ≤ x) by simulating a large number of Y values and finding the proportion that are less than x: > Y <- rnorm(100000) # a large number of standard normals > sum(Y < 2)/100000 # the proportion less than ...
... We can estimate the probability that a normal random variable Y is less than a given value, x: P (Y ≤ x) by simulating a large number of Y values and finding the proportion that are less than x: > Y <- rnorm(100000) # a large number of standard normals > sum(Y < 2)/100000 # the proportion less than ...
Expected value
In probability theory, the expected value of a random variable is intuitively the long-run average value of repetitions of the experiment it represents. For example, the expected value of a dice roll is 3.5 because, roughly speaking, the average of an extremely large number of dice rolls is practically always nearly equal to 3.5. Less roughly, the law of large numbers guarantees that the arithmetic mean of the values almost surely converges to the expected value as the number of repetitions goes to infinity. The expected value is also known as the expectation, mathematical expectation, EV, mean, or first moment.More practically, the expected value of a discrete random variable is the probability-weighted average of all possible values. In other words, each possible value the random variable can assume is multiplied by its probability of occurring, and the resulting products are summed to produce the expected value. The same works for continuous random variables, except the sum is replaced by an integral and the probabilities by probability densities. The formal definition subsumes both of these and also works for distributions which are neither discrete nor continuous: the expected value of a random variable is the integral of the random variable with respect to its probability measure.The expected value does not exist for random variables having some distributions with large ""tails"", such as the Cauchy distribution. For random variables such as these, the long-tails of the distribution prevent the sum/integral from converging.The expected value is a key aspect of how one characterizes a probability distribution; it is one type of location parameter. By contrast, the variance is a measure of dispersion of the possible values of the random variable around the expected value. The variance itself is defined in terms of two expectations: it is the expected value of the squared deviation of the variable's value from the variable's expected value.The expected value plays important roles in a variety of contexts. In regression analysis, one desires a formula in terms of observed data that will give a ""good"" estimate of the parameter giving the effect of some explanatory variable upon a dependent variable. The formula will give different estimates using different samples of data, so the estimate it gives is itself a random variable. A formula is typically considered good in this context if it is an unbiased estimator—that is, if the expected value of the estimate (the average value it would give over an arbitrarily large number of separate samples) can be shown to equal the true value of the desired parameter.In decision theory, and in particular in choice under uncertainty, an agent is described as making an optimal choice in the context of incomplete information. For risk neutral agents, the choice involves using the expected values of uncertain quantities, while for risk averse agents it involves maximizing the expected value of some objective function such as a von Neumann-Morgenstern utility function. One example of using expected value in reaching optimal decisions is the Gordon-Loeb Model of information security investment. According to the model, one can conclude that the amount a firm spends to protect information should generally be only a small fraction of the expected loss (i.e., the expected value of the loss resulting from a cyber/information security breach).