PDF
... there is an established notion of infinite simplicial complexes, the geometrical treatment of simplicial complexes is much simpler in the finite case and so for now we will assume that V is a finite set of cardinality k. We introduce the vector space RV of formal R–linear combinations of elements of ...
... there is an established notion of infinite simplicial complexes, the geometrical treatment of simplicial complexes is much simpler in the finite case and so for now we will assume that V is a finite set of cardinality k. We introduce the vector space RV of formal R–linear combinations of elements of ...
Selected Response and Written Response Pre and
... Multiple Choice. For questions 1-10, circle the letter of the correct answer. (2 points each) 1. Which congruence property is being demonstrated in the following statement? AB ≅ AB A. Reflexive B. Symmetric C. Transitive 2. Which congruence property is being demonstrated in the following statement? ...
... Multiple Choice. For questions 1-10, circle the letter of the correct answer. (2 points each) 1. Which congruence property is being demonstrated in the following statement? AB ≅ AB A. Reflexive B. Symmetric C. Transitive 2. Which congruence property is being demonstrated in the following statement? ...
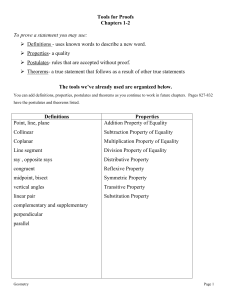
Proving Statements in Geometry
... • Lines a and b are parallel • We CANNOT assume... • We CANNOT assume... • Triangle ABC is a right triangle ...
... • Lines a and b are parallel • We CANNOT assume... • We CANNOT assume... • Triangle ABC is a right triangle ...
PPSection 2.5
... which lead from the given information to the conclusion which we are proving. In the right hand column, we give a reason why each statement is true. Since we list the given information first, our Given Any other first reason will always be ___________. reason must be a _________________, Definition ...
... which lead from the given information to the conclusion which we are proving. In the right hand column, we give a reason why each statement is true. Since we list the given information first, our Given Any other first reason will always be ___________. reason must be a _________________, Definition ...
Strategic Analysis AGRE PPT - FREE GRE GMAT Online Class
... Power set Indicial equn Symmetric matrix are those who are commutative Power set properties Harmonic complex function Fields & Rings (Abstract Algebra) Permutation group Chebyshev's theorem probability ...
... Power set Indicial equn Symmetric matrix are those who are commutative Power set properties Harmonic complex function Fields & Rings (Abstract Algebra) Permutation group Chebyshev's theorem probability ...
File - Miss Pereira
... An important part of writing a proof is giving justifications to show that every step is valid. ...
... An important part of writing a proof is giving justifications to show that every step is valid. ...
Groups. - MIT Mathematics
... that groups were absolutely fundamental to all kinds of mathematics. Speaking about geometry in particular, he said that studying a certain kind of geometry means studying a certain kind of symmetry group: that you should specify the symmetries first, and they’ll tell you what the geometry is. In or ...
... that groups were absolutely fundamental to all kinds of mathematics. Speaking about geometry in particular, he said that studying a certain kind of geometry means studying a certain kind of symmetry group: that you should specify the symmetries first, and they’ll tell you what the geometry is. In or ...
Symmetric Spaces
... p ∈ M is an isolated fixed point of an involutive (its square but not the mapping itself is the identity) isometry sp of M . Or equivalently ∀p ∈ M there is some sp ∈ I(M ) with the properties: sp (p) = p, (dsp )p = −I. Example 1: Euclidean Space Let M = Rn with the Euclidean metric. The geodesic sym ...
... p ∈ M is an isolated fixed point of an involutive (its square but not the mapping itself is the identity) isometry sp of M . Or equivalently ∀p ∈ M there is some sp ∈ I(M ) with the properties: sp (p) = p, (dsp )p = −I. Example 1: Euclidean Space Let M = Rn with the Euclidean metric. The geodesic sym ...
Symmetric group
In abstract algebra, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutation operations that can be performed on n distinct symbols, and whose group operation is the composition of such permutation operations, which are defined as bijective functions from the set of symbols to itself. Since there are n! (n factorial) possible permutation operations that can be performed on a tuple composed of n symbols, it follows that the order (the number of elements) of the symmetric group Sn is n!.Although symmetric groups can be defined on infinite sets as well, this article discusses only the finite symmetric groups: their applications, their elements, their conjugacy classes, a finite presentation, their subgroups, their automorphism groups, and their representation theory. For the remainder of this article, ""symmetric group"" will mean a symmetric group on a finite set.The symmetric group is important to diverse areas of mathematics such as Galois theory, invariant theory, the representation theory of Lie groups, and combinatorics. Cayley's theorem states that every group G is isomorphic to a subgroup of the symmetric group on G.