8. Smoothness and the Zariski tangent space We want to give an
... intervals in R into the manifold. This definition lifts to algebraic geometry over C but not over any other field (for example a field of characteristic p). Classically tangent vectors are determined by taking derivatives, and the tangent space to a variety X at x is then the space of tangent direct ...
... intervals in R into the manifold. This definition lifts to algebraic geometry over C but not over any other field (for example a field of characteristic p). Classically tangent vectors are determined by taking derivatives, and the tangent space to a variety X at x is then the space of tangent direct ...
PDF
... However, h1 is abelian, and hence, the above follows directly from (??). Adapting this argument in the obvious fashion we can show that Dkn+1 g ⊂ Dk h. Since h is nilpotent, g must be nilpotent as well. QED Historical remark. In the traditional formulation of Engel’s theorem, the hypotheses are the ...
... However, h1 is abelian, and hence, the above follows directly from (??). Adapting this argument in the obvious fashion we can show that Dkn+1 g ⊂ Dk h. Since h is nilpotent, g must be nilpotent as well. QED Historical remark. In the traditional formulation of Engel’s theorem, the hypotheses are the ...
Fleury`s spanning dimension and chain conditions on non
... K is semisimple and so Rad(M ) = (V, 0, 0) and any non-small submodule of M contains (V, 0, 0). Thus any chain of non-small submodules of M can be considered a chain in M/(V, 0, 0) which is finite dimensional. Hence any chain of non-small submodules stops. M is not hollow as it has the two maximal s ...
... K is semisimple and so Rad(M ) = (V, 0, 0) and any non-small submodule of M contains (V, 0, 0). Thus any chain of non-small submodules of M can be considered a chain in M/(V, 0, 0) which is finite dimensional. Hence any chain of non-small submodules stops. M is not hollow as it has the two maximal s ...
Asymptotic cones - American Institute of Mathematics
... We had many questions about the expressive power of continuous logic in this setting. What language should we work with? What can actually be said in the theory of such a metric structure? (We will abbreviate continuous logic by cclogic.) We will work in an arbitrary complete metric space (Y, d) wit ...
... We had many questions about the expressive power of continuous logic in this setting. What language should we work with? What can actually be said in the theory of such a metric structure? (We will abbreviate continuous logic by cclogic.) We will work in an arbitrary complete metric space (Y, d) wit ...
Then find a basis of
... 4.1.2 Is the following subset of P2 a subsapce? Find a basis for it if it is. { p(t)| p(2) = 0} Yes. 0(2) = 0 so 0 is included. If p1 (2) = 0 and p2 (2) = 0 then (p1 + p2 )(2) = p1 (2) + p2 (2) = 0 + 0 = 0 so it is closed under addition. And if p(2) = 0 then (rp)(2) = rp(2) = r0 = 0, so it is close ...
... 4.1.2 Is the following subset of P2 a subsapce? Find a basis for it if it is. { p(t)| p(2) = 0} Yes. 0(2) = 0 so 0 is included. If p1 (2) = 0 and p2 (2) = 0 then (p1 + p2 )(2) = p1 (2) + p2 (2) = 0 + 0 = 0 so it is closed under addition. And if p(2) = 0 then (rp)(2) = rp(2) = r0 = 0, so it is close ...
Counting Kings
... Definition 1. F (n) = the number of distinct configurations of non-attacking kings on a one-dimensional chess board with n squares. Consider F (n). Every configuration on a board of length n will either begin with an empty square or begin with a square with a king in it. Those that begin with an emp ...
... Definition 1. F (n) = the number of distinct configurations of non-attacking kings on a one-dimensional chess board with n squares. Consider F (n). Every configuration on a board of length n will either begin with an empty square or begin with a square with a king in it. Those that begin with an emp ...
SECTION 12: HOMOTOPY EXTENSION AND LIFTING PROPERTY
... Next, we will discuss the relation between Serre fibrations and relative CW complexes in terms of lifting properties. Recall that, by definition, a Serre fibration is a map having the right-liftingproperty (RLP) with respect to inclusions of the form I n × {0} → I n+1 ; or equivalently, with respect ...
... Next, we will discuss the relation between Serre fibrations and relative CW complexes in terms of lifting properties. Recall that, by definition, a Serre fibration is a map having the right-liftingproperty (RLP) with respect to inclusions of the form I n × {0} → I n+1 ; or equivalently, with respect ...
Dimensional Analysis - University of Michigan
... SECTION III PROBLEMS Here are several practice problems. The answers are at the end of the module. 27) How many seconds in 800 minutes? 28) How many dozens of eggs are there in 3,500 eggs? 29) How many minutes in five years? 30) What is the cost of six onions if three onions weigh 1.5 lb. and the p ...
... SECTION III PROBLEMS Here are several practice problems. The answers are at the end of the module. 27) How many seconds in 800 minutes? 28) How many dozens of eggs are there in 3,500 eggs? 29) How many minutes in five years? 30) What is the cost of six onions if three onions weigh 1.5 lb. and the p ...
Reading Dimensions Using a Standard Ruler
... What is the dimension represented by X above? 1. What is the smallest ruler increment represented for dimension X? 2. How many whole numbers are represented in dimension X? 3. How many increments are past the 2 inch mark? Dimension X is 13 increments past the whole number 2 ...
... What is the dimension represented by X above? 1. What is the smallest ruler increment represented for dimension X? 2. How many whole numbers are represented in dimension X? 3. How many increments are past the 2 inch mark? Dimension X is 13 increments past the whole number 2 ...
Thompson`s Group F is not SCY
... difficulty lies in the fact that the constraint on the first virtual Betti number, that is often very effective, is inconclusive: Proposition. Thompson’s group F satisfies b1 (F ) = vb1 (F ) = 2. Proof. This is a consequence of the fact that ([CFP96, Theorems 4.5]) the commutator subgroup [F, F ] is ...
... difficulty lies in the fact that the constraint on the first virtual Betti number, that is often very effective, is inconclusive: Proposition. Thompson’s group F satisfies b1 (F ) = vb1 (F ) = 2. Proof. This is a consequence of the fact that ([CFP96, Theorems 4.5]) the commutator subgroup [F, F ] is ...
symmetry properties of sasakian space forms
... space of constant curvature one. Theorem 2.2.([15]) A Sasakian manifold is semi-symmetric if and only if it is a space of constant curvature one. Theorem 2.3. Every Sasakian space forms M 2n+1 (c) is pseudo-symmetric, more precisely for every Sasakian space forms: R · R = Q(g, R). Proof. As is well ...
... space of constant curvature one. Theorem 2.2.([15]) A Sasakian manifold is semi-symmetric if and only if it is a space of constant curvature one. Theorem 2.3. Every Sasakian space forms M 2n+1 (c) is pseudo-symmetric, more precisely for every Sasakian space forms: R · R = Q(g, R). Proof. As is well ...
the orbit spaces of totally disconnected groups of transformations on
... 1 and 2 we may state in terms of dimension a criterion for a compact group of transformations to be a Lie group. We state the corollary here. Its proof is the last part of the paper. ...
... 1 and 2 we may state in terms of dimension a criterion for a compact group of transformations to be a Lie group. We state the corollary here. Its proof is the last part of the paper. ...
Finitistic Spaces and Dimension
... an open refinement of finite order. This is a contradiction. Next, let F be a closed subset of X which does not meet K. By the point finite sum theorem for dim ([9, Theorem 3.1.13] or [9, Theorem 3.1.14]), it suffices to show that F ⊂ Pn for some n. Suppose on the contrary. Then we may have a sequen ...
... an open refinement of finite order. This is a contradiction. Next, let F be a closed subset of X which does not meet K. By the point finite sum theorem for dim ([9, Theorem 3.1.13] or [9, Theorem 3.1.14]), it suffices to show that F ⊂ Pn for some n. Suppose on the contrary. Then we may have a sequen ...
Dimension Theory
... remembered, will skill you to answer that elusive GCSE question if it happens to appear this year! ...
... remembered, will skill you to answer that elusive GCSE question if it happens to appear this year! ...
Lect08_similarity
... Dimensions of any other variables can be represented by these fundamental dimensions. Example ...
... Dimensions of any other variables can be represented by these fundamental dimensions. Example ...
Chapter 7 - U.I.U.C. Math
... 4. If 0 → Kn−1 → Xn−1 → · · · → X0 → M → 0 is an exact sequence with all Xi projective, then Kn−1 is projective. Proof. To show that (1) implies (2), observe that by hypothesis, there is a projective resolution 0 → Xn → · · · → X0 → M → 0. Use this resolution to compute Ext, and conclude that (2) ho ...
... 4. If 0 → Kn−1 → Xn−1 → · · · → X0 → M → 0 is an exact sequence with all Xi projective, then Kn−1 is projective. Proof. To show that (1) implies (2), observe that by hypothesis, there is a projective resolution 0 → Xn → · · · → X0 → M → 0. Use this resolution to compute Ext, and conclude that (2) ho ...
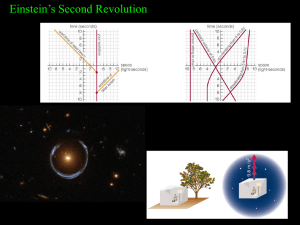
Day 3 Sections S3.1-3 Spacetime, A New View of Gravity
... 3) Astronaut Bill is hovering 15,000,000 miles above a neutron star while astronaut Susan is down close the surface making measurements. When Bill compares his clock to Susan’s, he says her clock is running slower than his. What does Susan say when she compares her clock to Bill’s? ...
... 3) Astronaut Bill is hovering 15,000,000 miles above a neutron star while astronaut Susan is down close the surface making measurements. When Bill compares his clock to Susan’s, he says her clock is running slower than his. What does Susan say when she compares her clock to Bill’s? ...
Dimension

In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it – for example, the point at 5 on a number line. A surface such as a plane or the surface of a cylinder or sphere has a dimension of two because two coordinates are needed to specify a point on it – for example, both a latitude and longitude are required to locate a point on the surface of a sphere. The inside of a cube, a cylinder or a sphere is three-dimensional because three coordinates are needed to locate a point within these spaces.In classical mechanics, space and time are different categories and refer to absolute space and time. That conception of the world is a four-dimensional space but not the one that was found necessary to describe electromagnetism. The four dimensions of spacetime consist of events that are not absolutely defined spatially and temporally, but rather are known relative to the motion of an observer. Minkowski space first approximates the universe without gravity; the pseudo-Riemannian manifolds of general relativity describe spacetime with matter and gravity. Ten dimensions are used to describe string theory, and the state-space of quantum mechanics is an infinite-dimensional function space.The concept of dimension is not restricted to physical objects. High-dimensional spaces frequently occur in mathematics and the sciences. They may be parameter spaces or configuration spaces such as in Lagrangian or Hamiltonian mechanics; these are abstract spaces, independent of the physical space we live in.