Open problems on Cherednik algebras, symplectic reflection
... coming from quantized algebraic surfaces, and to give meaning to this deformation for non-formal (i.e., numerical) values of parameters. One expects that the “spherical subalgebra” eHn,k (Au)e (where e ∈ C[Sn] is the Young symmetrizer) will then be a quantization of the Hilbert scheme of the corresp ...
... coming from quantized algebraic surfaces, and to give meaning to this deformation for non-formal (i.e., numerical) values of parameters. One expects that the “spherical subalgebra” eHn,k (Au)e (where e ∈ C[Sn] is the Young symmetrizer) will then be a quantization of the Hilbert scheme of the corresp ...
Lecture 14: Bordism categories The definition Fix a nonnegative1
... X ◦ Xf ◦ X ∨ ≃ Klein bottle ...
... X ◦ Xf ◦ X ∨ ≃ Klein bottle ...
EE Pacing Guide - essentialelementsutah
... C2.1 I can use properties of geometric shapes to describe real-life objects. (9th) C2.2 I can determine the area, perimeter, and volume (rectangles, triangles, prisms) to solve real world problems. (9th) C3.2 I can compare graph or table from given categorical data. (8th) C3.2 I can describe the pro ...
... C2.1 I can use properties of geometric shapes to describe real-life objects. (9th) C2.2 I can determine the area, perimeter, and volume (rectangles, triangles, prisms) to solve real world problems. (9th) C3.2 I can compare graph or table from given categorical data. (8th) C3.2 I can describe the pro ...
Irrationality Exponent, Hausdorff Dimension and Effectivization
... h(σ) = τ . There is a universal computable function u with the property that for every such h there is a constant c such that for all τ , the h-complexity of τ is less than the u-complexity of τ plus c. Fix a universal u and define the prefix-free Kolmogorov complexity of τ be its u-complexity. In t ...
... h(σ) = τ . There is a universal computable function u with the property that for every such h there is a constant c such that for all τ , the h-complexity of τ is less than the u-complexity of τ plus c. Fix a universal u and define the prefix-free Kolmogorov complexity of τ be its u-complexity. In t ...
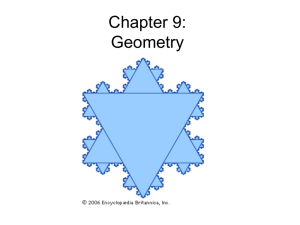
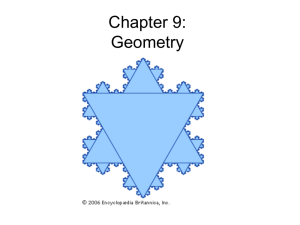
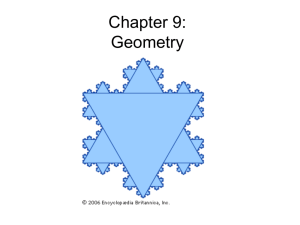
chapter 9
... the fifth, and for many years it was thought that the fifth could be derived from the first four • It was finally proven that the fifth postulate is an axiom and is consistent with the first four, but NOT necessary (took more than 2000 years!) • Saccheri (1667-1733) made the most dedicated attempt w ...
... the fifth, and for many years it was thought that the fifth could be derived from the first four • It was finally proven that the fifth postulate is an axiom and is consistent with the first four, but NOT necessary (took more than 2000 years!) • Saccheri (1667-1733) made the most dedicated attempt w ...
Solutions
... of non-empty open T sets {Uα1 , · · · , Uαn , · · · } such that Uαi+1 * j6i Uαj for all i. Let Yi = j6i Uαc j . Then Y1 ⊃ Y2 ⊃ · · · does not satisfy the descending chain condition for closed subsets. (b) Recall that we say X has the discrete topology if every subset of X is open (closed). Now let X ...
... of non-empty open T sets {Uα1 , · · · , Uαn , · · · } such that Uαi+1 * j6i Uαj for all i. Let Yi = j6i Uαc j . Then Y1 ⊃ Y2 ⊃ · · · does not satisfy the descending chain condition for closed subsets. (b) Recall that we say X has the discrete topology if every subset of X is open (closed). Now let X ...
THE HITCHIN FIBRATION Here X is a smooth connected projective
... is a morphism which defines a complete integrable system (in the algebraic setting): the fiber over a general a ∈ ⊕ri=2 H0 (X, ωi ) is Lagrangian and of the same dimension as SLr (X, δ)◦ . Moreover, the resulting Hamiltonian action on that fiber factors through the Prym variety of the spectral cover ...
... is a morphism which defines a complete integrable system (in the algebraic setting): the fiber over a general a ∈ ⊕ri=2 H0 (X, ωi ) is Lagrangian and of the same dimension as SLr (X, δ)◦ . Moreover, the resulting Hamiltonian action on that fiber factors through the Prym variety of the spectral cover ...
Symplectic Topology
... for R k = R l × R k−l (or simplify by φ 7→ f ). Theorem (Lie): If such a symmetry group is finite-dimensional and compact it’s SO(n), or SU (n) or SP (n) or one of a finite list of exceptions. [Drop compactness: get SO(p, q), SO(n, C ) etc, but still finitely many families.] Theorem (Cartan): If the ...
... for R k = R l × R k−l (or simplify by φ 7→ f ). Theorem (Lie): If such a symmetry group is finite-dimensional and compact it’s SO(n), or SU (n) or SP (n) or one of a finite list of exceptions. [Drop compactness: get SO(p, q), SO(n, C ) etc, but still finitely many families.] Theorem (Cartan): If the ...
Sample Book - Career Point Kota
... Whenever a student decides to prepare for any examination, her/his first and foremost curiosity about the type of questions that he/she has to face. This becomes more important in the context of competitive examinations where there is neck-to-neck race. We feel great pleasure to present before you t ...
... Whenever a student decides to prepare for any examination, her/his first and foremost curiosity about the type of questions that he/she has to face. This becomes more important in the context of competitive examinations where there is neck-to-neck race. We feel great pleasure to present before you t ...
fractal
... Dimension of fractals • Fractals have infinite length but occupied in finite region • Lets apply this concept for simple line, square, and cube. • A straight line having unit length is divided into N equal segments, then length of each side is r = 1/N • A square having unit length sides, divided in ...
... Dimension of fractals • Fractals have infinite length but occupied in finite region • Lets apply this concept for simple line, square, and cube. • A straight line having unit length is divided into N equal segments, then length of each side is r = 1/N • A square having unit length sides, divided in ...
Spencer Bloch: The proof of the Mordell Conjecture
... chapter in n u m b e r theory. In fact, his paper also es- in a vector space of dimension n + 1. If we fix a basis tablishes two other important conjectures, due to Tate of the vector space we can specify a line, and hence a a n d Shafarevich, a n d these a c h i e v e m e n t s m a y well point of ...
... chapter in n u m b e r theory. In fact, his paper also es- in a vector space of dimension n + 1. If we fix a basis tablishes two other important conjectures, due to Tate of the vector space we can specify a line, and hence a a n d Shafarevich, a n d these a c h i e v e m e n t s m a y well point of ...
Cumrun Vafa
... non-trivial CFT’s in higher dimensions. However, the assumption of supersymmetry becomes more powerful as we go up in dimension: The highest dimension for a conformal field theory which enjoys supersymmetry is 6 dimensions. (related to the fact that conformal group is SO(6,2) and triality of so(8) p ...
... non-trivial CFT’s in higher dimensions. However, the assumption of supersymmetry becomes more powerful as we go up in dimension: The highest dimension for a conformal field theory which enjoys supersymmetry is 6 dimensions. (related to the fact that conformal group is SO(6,2) and triality of so(8) p ...
Sublinear Algorithms Course
... Testing if a List is Sorted Input: a list of n numbers x1 , x2 ,..., xn • Question: Is the list sorted? Requires reading entire list: (n) time • Approximate version: Is the list sorted or ²-far from sorted? (An ² fraction of xi ’s have to be changed to make it sorted.) [Ergün Kannan Kumar Rubinfel ...
... Testing if a List is Sorted Input: a list of n numbers x1 , x2 ,..., xn • Question: Is the list sorted? Requires reading entire list: (n) time • Approximate version: Is the list sorted or ²-far from sorted? (An ² fraction of xi ’s have to be changed to make it sorted.) [Ergün Kannan Kumar Rubinfel ...
REMARKS ON WILMSHURST`S THEOREM 1. Introduction Suppose
... We state the counterexamples in Section 2 and prove this estimate on the number of zeros. In Section 3, we give an alternative proof of Wilmshurst’s theorem that relies more heavily on real algebraic geometry and readily generalizes to harmonic vector fields in higher dimensions but with a weaker co ...
... We state the counterexamples in Section 2 and prove this estimate on the number of zeros. In Section 3, we give an alternative proof of Wilmshurst’s theorem that relies more heavily on real algebraic geometry and readily generalizes to harmonic vector fields in higher dimensions but with a weaker co ...
zero and infinity in the non euclidean geometry
... We should avoid and fear the matter of the parallels as well as we should avoid and fear the matter of the passions. It is also able to take all your time and your happiness, depriving you of your good health.” Farkas Bolyai to his son Janos ...
... We should avoid and fear the matter of the parallels as well as we should avoid and fear the matter of the passions. It is also able to take all your time and your happiness, depriving you of your good health.” Farkas Bolyai to his son Janos ...
http://www.math.uni-muenster.de/u/lueck/publ/lueck/surveyclassi04.pdf
... which there exists an open covering {Ui | i ∈ I} by G-subspaces such that there is for each i ∈ I a G-map Ui → G/Gi for some Gi ∈ F and there is a locally finite partition of unity {ei | i ∈ I} subordinate to {Ui | i ∈ I} by G-invariant functions ei : X → [0, 1]. Notice that we do not demand that th ...
... which there exists an open covering {Ui | i ∈ I} by G-subspaces such that there is for each i ∈ I a G-map Ui → G/Gi for some Gi ∈ F and there is a locally finite partition of unity {ei | i ∈ I} subordinate to {Ui | i ∈ I} by G-invariant functions ei : X → [0, 1]. Notice that we do not demand that th ...
Closed locally path-connected subspaces of finite
... not homeomorphic to closed subspaces of finite-dimensional topological groups. First we state a Key Lemma treating locally continuum-connected subspaces of finite-dimensional topological groups. By a continuum we understand a connected compact Hausdorff space. We shall say that two points x, y of a top ...
... not homeomorphic to closed subspaces of finite-dimensional topological groups. First we state a Key Lemma treating locally continuum-connected subspaces of finite-dimensional topological groups. By a continuum we understand a connected compact Hausdorff space. We shall say that two points x, y of a top ...
area - StFX
... the fifth, and for many years it was thought that the fifth could be derived from the first four • It was finally proven that the fifth postulate is an axiom and is consistent with the first four, but NOT necessary (took more than 2000 years!) • Saccheri (1667-1733) made the most dedicated attempt w ...
... the fifth, and for many years it was thought that the fifth could be derived from the first four • It was finally proven that the fifth postulate is an axiom and is consistent with the first four, but NOT necessary (took more than 2000 years!) • Saccheri (1667-1733) made the most dedicated attempt w ...
chapter 9
... the fifth, and for many years it was thought that the fifth could be derived from the first four • It was finally proven that the fifth postulate is an axiom and is consistent with the first four, but NOT necessary (took more than 2000 years!) • Saccheri (1667-1733) made the most dedicated attempt w ...
... the fifth, and for many years it was thought that the fifth could be derived from the first four • It was finally proven that the fifth postulate is an axiom and is consistent with the first four, but NOT necessary (took more than 2000 years!) • Saccheri (1667-1733) made the most dedicated attempt w ...
Dimension

In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it – for example, the point at 5 on a number line. A surface such as a plane or the surface of a cylinder or sphere has a dimension of two because two coordinates are needed to specify a point on it – for example, both a latitude and longitude are required to locate a point on the surface of a sphere. The inside of a cube, a cylinder or a sphere is three-dimensional because three coordinates are needed to locate a point within these spaces.In classical mechanics, space and time are different categories and refer to absolute space and time. That conception of the world is a four-dimensional space but not the one that was found necessary to describe electromagnetism. The four dimensions of spacetime consist of events that are not absolutely defined spatially and temporally, but rather are known relative to the motion of an observer. Minkowski space first approximates the universe without gravity; the pseudo-Riemannian manifolds of general relativity describe spacetime with matter and gravity. Ten dimensions are used to describe string theory, and the state-space of quantum mechanics is an infinite-dimensional function space.The concept of dimension is not restricted to physical objects. High-dimensional spaces frequently occur in mathematics and the sciences. They may be parameter spaces or configuration spaces such as in Lagrangian or Hamiltonian mechanics; these are abstract spaces, independent of the physical space we live in.