Chapter 3, Groups
... If we look at Propositions 1.9 and 2.14, we can see that the composition of maps in Sn and the sum in Z/nZ have some common properties: Both operations are associative, have an identity element (Id for the composition of maps, 0 for the sum), and every element has an inverse. It turns out that it is ...
... If we look at Propositions 1.9 and 2.14, we can see that the composition of maps in Sn and the sum in Z/nZ have some common properties: Both operations are associative, have an identity element (Id for the composition of maps, 0 for the sum), and every element has an inverse. It turns out that it is ...
Algebra 411 Homework 5: hints and solutions
... f (x) + f (y), any isomorphism is completely determined by where we send 1 to. In other words, if we choose f (1) = 1, then since f (1 + 1) = f (1) + f (1), it follows that f (2) = 2, and likewise f (3) = 3, f (0) = 0. Similarly if we had started from f (1) = 3, we would get the second isomorphism. ...
... f (x) + f (y), any isomorphism is completely determined by where we send 1 to. In other words, if we choose f (1) = 1, then since f (1 + 1) = f (1) + f (1), it follows that f (2) = 2, and likewise f (3) = 3, f (0) = 0. Similarly if we had started from f (1) = 3, we would get the second isomorphism. ...
Solutions to Practice Quiz 6
... 5. Let G = Z4 ⊕ Z4 , and consider the subgroups H = {(0, 0), (2, 0), (0, 2), (2, 2)} and K = h(1, 2)i. Identify the following groups (as direct products of cyclic groups of prime order): (a) H and G/H. Clearly, H ∼ = Z2 ⊕ Z2 . Moreover, G/H ∼ = Z2 ⊕ Z2 ; indeed, the assignment (0, 1) 7→ (0, 1) and ( ...
... 5. Let G = Z4 ⊕ Z4 , and consider the subgroups H = {(0, 0), (2, 0), (0, 2), (2, 2)} and K = h(1, 2)i. Identify the following groups (as direct products of cyclic groups of prime order): (a) H and G/H. Clearly, H ∼ = Z2 ⊕ Z2 . Moreover, G/H ∼ = Z2 ⊕ Z2 ; indeed, the assignment (0, 1) 7→ (0, 1) and ( ...
Math 3121 Lecture 6 ppt97
... Theorem: Let G be a group. The intersection of a set of subgroups of G is a subgroup of G. Proof: Let T be a set of subgroups of G, and let H be the intersection of all members of T. Then h is in H if and only if h is in K for all K in T. Now we show that H satisfies the conditions in the theorem fo ...
... Theorem: Let G be a group. The intersection of a set of subgroups of G is a subgroup of G. Proof: Let T be a set of subgroups of G, and let H be the intersection of all members of T. Then h is in H if and only if h is in K for all K in T. Now we show that H satisfies the conditions in the theorem fo ...
Groups - CSE-IITK
... other elements can be constructed with x. The composition with identity will not give anything new, so lets compose it with itself. Since G is a group, x2 := x ∗ x, x3 := x2 ∗ x (notice the new notation) and so on will be elements of group G. In this way we can create new elements in G except if the ...
... other elements can be constructed with x. The composition with identity will not give anything new, so lets compose it with itself. Since G is a group, x2 := x ∗ x, x3 := x2 ∗ x (notice the new notation) and so on will be elements of group G. In this way we can create new elements in G except if the ...
Conics The conics get their name from the fact that they can be
... The sum of the distances to any point on the ellipse (x,y) from the two foci (c,0) and (-c,0) is a constant. That constant will be 2a. If we let d1 and d2 be the distances from the foci to the point, then d1 + d2 = 2a. The ellipse is a stretched circle. Begin with the unit circle (circle with a radi ...
... The sum of the distances to any point on the ellipse (x,y) from the two foci (c,0) and (-c,0) is a constant. That constant will be 2a. If we let d1 and d2 be the distances from the foci to the point, then d1 + d2 = 2a. The ellipse is a stretched circle. Begin with the unit circle (circle with a radi ...
On a theorem of Blichfeldt
... As a byproduct of the proof we observe that F1 (G) is the number of orbits of G. This is a well-known formula sometimes (inaccurately) called Burnside’s Lemma (see [13]). If there is only one orbit, the group is called transitive. In this case, F2 (G) is the rank of G, i. e. the number of orbits of ...
... As a byproduct of the proof we observe that F1 (G) is the number of orbits of G. This is a well-known formula sometimes (inaccurately) called Burnside’s Lemma (see [13]). If there is only one orbit, the group is called transitive. In this case, F2 (G) is the rank of G, i. e. the number of orbits of ...
MATH 120, SOLUTION SET #6 §3.5 15: Let H = 〈x〉 and K = 〈y
... With that in mind, here is an example. Let K be all translations of the plane. As our H we can take all horizontal translations, and as H 0 all vertical translations. We need G to contain an element g such that g(a horizontal translation)g −1 must be a vertical translation. Rotation by 90 degrees (a ...
... With that in mind, here is an example. Let K be all translations of the plane. As our H we can take all horizontal translations, and as H 0 all vertical translations. We need G to contain an element g such that g(a horizontal translation)g −1 must be a vertical translation. Rotation by 90 degrees (a ...
on the burnside problem on periodic groups
... and F£, is the normal subgroup of ¥m generated by all nth powers (with odd n > 4381) of elements of Fm, were constructed and studied. Using a very complicated inductive construction, Novikov and Adian presented the group B(m, n) by defining relations of the form A" — 1, where A's are some specially ...
... and F£, is the normal subgroup of ¥m generated by all nth powers (with odd n > 4381) of elements of Fm, were constructed and studied. Using a very complicated inductive construction, Novikov and Adian presented the group B(m, n) by defining relations of the form A" — 1, where A's are some specially ...
Chapter 2
... 1) The product of any 2 elements in a group and the square of each element must also be a member of the group. Note that here, the word “product” does not necessarily mean ‘multiply’ in the traditional sense of the word (e.g. 2*3 = 6). You can think of the word product as meaning “act on” or “operat ...
... 1) The product of any 2 elements in a group and the square of each element must also be a member of the group. Note that here, the word “product” does not necessarily mean ‘multiply’ in the traditional sense of the word (e.g. 2*3 = 6). You can think of the word product as meaning “act on” or “operat ...
Solutions 8 - D-MATH
... that H is a proper subgroup since no word on {ab, ba} can have odd length, and that it has index two as H ∪ aH. 3. A finite list of generators is given by taking all the elements of the group - there are only finitely many. The composition of two elements g1 and g2 of the group under the group’s law ...
... that H is a proper subgroup since no word on {ab, ba} can have odd length, and that it has index two as H ∪ aH. 3. A finite list of generators is given by taking all the elements of the group - there are only finitely many. The composition of two elements g1 and g2 of the group under the group’s law ...
ABSTRACT : GROUP THEORY
... In Abelian groups, each element is in a class' by itself, since XAX-1 = AXX-' = AE = A. If the group elements are represented by matrices, the traces of all elements in a class must be the same. This follows, since in this case ths operation of conjugation becomes that of making a similarity transfo ...
... In Abelian groups, each element is in a class' by itself, since XAX-1 = AXX-' = AE = A. If the group elements are represented by matrices, the traces of all elements in a class must be the same. This follows, since in this case ths operation of conjugation becomes that of making a similarity transfo ...
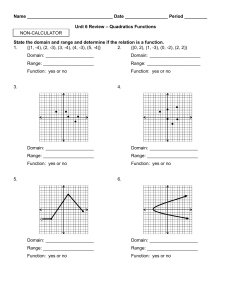
review: quadratics
... Write the equation for the function y = x2 with the following transformations. 20. shift right 4 and up 2 21. reflect across the x-axis, shift left 2 ...
... Write the equation for the function y = x2 with the following transformations. 20. shift right 4 and up 2 21. reflect across the x-axis, shift left 2 ...
Solution - UC Davis Mathematics
... in the line {x = y}. Present the transformation A, B, AB, BA by matrices, describe AB and BA geometrically. Solution: ...
... in the line {x = y}. Present the transformation A, B, AB, BA by matrices, describe AB and BA geometrically. Solution: ...
Physics 129B, Winter 2010 Problem Set 1 Solution
... This should be the multiplication table for all groups of order 2, because we made no assumption for the group except that it is of order 2. So all groups of order 2, one of which is C2 , are isomorphic to one another. Next, consider a group of order 3, which has three elements e, a, and b. We can s ...
... This should be the multiplication table for all groups of order 2, because we made no assumption for the group except that it is of order 2. So all groups of order 2, one of which is C2 , are isomorphic to one another. Next, consider a group of order 3, which has three elements e, a, and b. We can s ...
2. Examples of Groups 2.1. Some infinite abelian groups. It is easy to
... Let us consider first D3 : D3 has 6 elements, namely the identity ι, two non-trivial rotations say ρ1 and ρ2 , and three reflections say σ1 , σ2 , and σ3 . If we label the vertices of the regular triangle with 1, 2, and 3, then every permutation of {1, 2, 3} corresponds to an element of D3 , and sin ...
... Let us consider first D3 : D3 has 6 elements, namely the identity ι, two non-trivial rotations say ρ1 and ρ2 , and three reflections say σ1 , σ2 , and σ3 . If we label the vertices of the regular triangle with 1, 2, and 3, then every permutation of {1, 2, 3} corresponds to an element of D3 , and sin ...
Notes
... A subset H ⊂ G is a subgroup if H is a group by using the binary operation of G, denoted H < G. Example 1.1.2. Let G = (R, +). The subset S = R − {0} ⊂ G is a group under multiplication. But it is not a subgroup of G because the operation on S is different from the one on G. Let K = Z. Then K is a s ...
... A subset H ⊂ G is a subgroup if H is a group by using the binary operation of G, denoted H < G. Example 1.1.2. Let G = (R, +). The subset S = R − {0} ⊂ G is a group under multiplication. But it is not a subgroup of G because the operation on S is different from the one on G. Let K = Z. Then K is a s ...
Orderable groups with applications to topology Dale
... Remark: These examples all have nontrivial, finite first homology (recalling H1 is the abelianization of π1): |H1(M )| = 16|p + q − r − s|. Therefore this construction gives infinitely many distinct examples of 3-manifolds with non-LO fundamental groups. Their fundamental groups are, however, torsi ...
... Remark: These examples all have nontrivial, finite first homology (recalling H1 is the abelianization of π1): |H1(M )| = 16|p + q − r − s|. Therefore this construction gives infinitely many distinct examples of 3-manifolds with non-LO fundamental groups. Their fundamental groups are, however, torsi ...
1. Direct products and finitely generated abelian groups We would
... namely cyclic groups, and we know they are all isomorphic to Zn if they are finite and the only infinite cyclic group is Z, up to isomorphism. Is this all? No, the Klein 4-group has order four, so it is definitely finitely generated, it is abelian and yet it is not cyclic, since every element has or ...
... namely cyclic groups, and we know they are all isomorphic to Zn if they are finite and the only infinite cyclic group is Z, up to isomorphism. Is this all? No, the Klein 4-group has order four, so it is definitely finitely generated, it is abelian and yet it is not cyclic, since every element has or ...
UNT UTA Algebra Symposium University of North Texas November
... Consider a finite, unitary reflection group G acting on a complex vector space V and an element X in the lattice of the associated hyperplane arrangement. Let N be the setwise stabilizer of X in G, Z the pointwise stabilizer, and C=N/Z. Restriction defines a homomorphism from the algebra of G-invari ...
... Consider a finite, unitary reflection group G acting on a complex vector space V and an element X in the lattice of the associated hyperplane arrangement. Let N be the setwise stabilizer of X in G, Z the pointwise stabilizer, and C=N/Z. Restriction defines a homomorphism from the algebra of G-invari ...
PH Kropholler Olympia Talelli
... of the coinduced module CoindyH and contains G-fixed points in the form of the constant functions. The action of G is given by @(g’) = 4( gg’). We prove that Z is ZF-free for each finite F using a result of Nobeling that [s2, Z] is free abelian for any set 0; see [ 1, Corollary 97.41. Let F be a fin ...
... of the coinduced module CoindyH and contains G-fixed points in the form of the constant functions. The action of G is given by @(g’) = 4( gg’). We prove that Z is ZF-free for each finite F using a result of Nobeling that [s2, Z] is free abelian for any set 0; see [ 1, Corollary 97.41. Let F be a fin ...
. - Humble ISD
... The graph shows repeated translations that result in the animation of the raindrop. Describe the translation of the raindrop from position 3 to position 4 using a translation vector < a , b >. ...
... The graph shows repeated translations that result in the animation of the raindrop. Describe the translation of the raindrop from position 3 to position 4 using a translation vector < a , b >. ...
Point set alignment - Department of Computer Science
... To minimize w.r.t. scale s, first term should be zero, or Scale ...
... To minimize w.r.t. scale s, first term should be zero, or Scale ...
F18PA2 Number Theory and Geometry: Tutorial 9
... (a) A half-turn is a rotation by angle π with centre some point C = (p, q) ∈ R2 . We denote it by hC . Find a formula for hC using the following facts: • hC is a direct isometry, • the angle θ in the formula for hC is equal to π, • hC fixes C. (b) Let P, Q, R be points on the x–axis in R2 . Show tha ...
... (a) A half-turn is a rotation by angle π with centre some point C = (p, q) ∈ R2 . We denote it by hC . Find a formula for hC using the following facts: • hC is a direct isometry, • the angle θ in the formula for hC is equal to π, • hC fixes C. (b) Let P, Q, R be points on the x–axis in R2 . Show tha ...