The circle group - Cambridge University Press
... group such that its proper closed subgroups are {g : gn = 1}, for n ranging over the set of all positive integers. Then G is topologically isomorphic to T . ...
... group such that its proper closed subgroups are {g : gn = 1}, for n ranging over the set of all positive integers. Then G is topologically isomorphic to T . ...
Amenable Actions of Nonamenable Groups
... 2. Suppose that G is generated by a finite generating set S and that the action is minimal on X , i.e., that every G-orbit is dense. Then for every G-regular point ξ the Schreier graph Γ (G, Gξ , S) is locally contained in the Schreier graph Γ (G, Gζ , S) for every ζ ∈ X . Here Gζ denotes the stabil ...
... 2. Suppose that G is generated by a finite generating set S and that the action is minimal on X , i.e., that every G-orbit is dense. Then for every G-regular point ξ the Schreier graph Γ (G, Gξ , S) is locally contained in the Schreier graph Γ (G, Gζ , S) for every ζ ∈ X . Here Gζ denotes the stabil ...
http://www.math.uni-muenster.de/u/lueck/publ/lueck/surveyclassi04.pdf
... Leary and Nucinkis have constructed many very interesting examples of discrete groups some of which are listed below. Their main technical input is an equivariant version of the constructions due to Bestvina and Brady. These examples show that the answer to the Problems 37 and to other problems appe ...
... Leary and Nucinkis have constructed many very interesting examples of discrete groups some of which are listed below. Their main technical input is an equivariant version of the constructions due to Bestvina and Brady. These examples show that the answer to the Problems 37 and to other problems appe ...
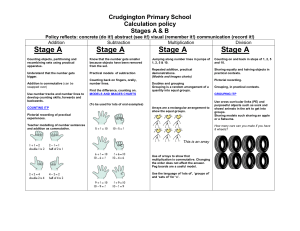
Calculation Policy Stage-ab - Crudgington Primary School
... Addition is the inverse of subtraction. Fact family. ...
... Addition is the inverse of subtraction. Fact family. ...
GROUP THEORY 1. Groups A set G is called a group if there is a
... An element x ∈ G is called central if xy = yx for all y ∈ G. The set ZG of all central elements is called the center of G. Let H ⊆ G be a subgroup. Define the normalizer NH of H as {g ∈ G| gHg −1 ⊆ H}. This is the smallest subgroup of G, in which H is normal. If S ⊆ G is an arbitrary subset, then d ...
... An element x ∈ G is called central if xy = yx for all y ∈ G. The set ZG of all central elements is called the center of G. Let H ⊆ G be a subgroup. Define the normalizer NH of H as {g ∈ G| gHg −1 ⊆ H}. This is the smallest subgroup of G, in which H is normal. If S ⊆ G is an arbitrary subset, then d ...
WORKING SEMINAR ON THE STRUCTURE OF LOCALLY
... (i) A smooth atlas is a set of local homeomorphisms (φα )α∈A from open subsets Uα , covering M , into Rn , and such that the transition maps φα ◦ φ−1 β are smooth whenever they are well defined. Two atlases are compatible if their union is still a smooth atlas. An equivalence class of atlas for the ...
... (i) A smooth atlas is a set of local homeomorphisms (φα )α∈A from open subsets Uα , covering M , into Rn , and such that the transition maps φα ◦ φ−1 β are smooth whenever they are well defined. Two atlases are compatible if their union is still a smooth atlas. An equivalence class of atlas for the ...
Slide 1
... • Proof. The operation of multiplying two cosets, Ng1 and Ng2, is defined in terms of particular elements, g1 and g2, of the cosets. For this operation to make sense, we have to verify that, if we choose different elements, h1 and h2, in the same cosets, the product coset N(h1 · h2) is the same as N ...
... • Proof. The operation of multiplying two cosets, Ng1 and Ng2, is defined in terms of particular elements, g1 and g2, of the cosets. For this operation to make sense, we have to verify that, if we choose different elements, h1 and h2, in the same cosets, the product coset N(h1 · h2) is the same as N ...
G - WordPress.com
... isomorphic if there is an isomorphism of G onto G’. We shall denote that G and G’ are isomorphic by writing G G’. ...
... isomorphic if there is an isomorphism of G onto G’. We shall denote that G and G’ are isomorphic by writing G G’. ...
isacker_a2
... Closure. If g1 and g2 belong to G, then g1g2 also belongs to G. Associativity. We always have (g1g2)g3=g1(g2g3). Existence of identity element. An element 1 exists such that g1=1g=g for all elements g of G. Existence of inverse element. For each element g of G, an inverse element g-1 exists s ...
... Closure. If g1 and g2 belong to G, then g1g2 also belongs to G. Associativity. We always have (g1g2)g3=g1(g2g3). Existence of identity element. An element 1 exists such that g1=1g=g for all elements g of G. Existence of inverse element. For each element g of G, an inverse element g-1 exists s ...
Nilpotent groups
... HW4.ex01: Prove this lemma (in your own words) and discuss the question: Is this true for infinite products? Ans: [by Georgi] It is enough to show that the product of two nilpotent groups is nilpotent. So suppose that G and H are nilpotent of class a, b resp. Let c = max(a, b). Then Z c (G) = G and ...
... HW4.ex01: Prove this lemma (in your own words) and discuss the question: Is this true for infinite products? Ans: [by Georgi] It is enough to show that the product of two nilpotent groups is nilpotent. So suppose that G and H are nilpotent of class a, b resp. Let c = max(a, b). Then Z c (G) = G and ...
Introduction to group theory
... The mapping between G and D(G) is called a homomorphism. If the mapping is one-to-one then it is called an isomorphism and D(G) is a faithful representation. In case the mapping is not into a set of matrices but into some other algebraic structure, it is called a realization. In general a group can ...
... The mapping between G and D(G) is called a homomorphism. If the mapping is one-to-one then it is called an isomorphism and D(G) is a faithful representation. In case the mapping is not into a set of matrices but into some other algebraic structure, it is called a realization. In general a group can ...
Math 3121 Lecture 4 Sections 5
... is a subgroup of G and is the smallest subgroup of G that contains a. Proof: See the book. Sketch: H satisfies the three properties for subgroups on the previous theorem. Thus is a subgroup. To prove any subgroup K of G that contains a must contain H: Let S be the set of all positive n such that an ...
... is a subgroup of G and is the smallest subgroup of G that contains a. Proof: See the book. Sketch: H satisfies the three properties for subgroups on the previous theorem. Thus is a subgroup. To prove any subgroup K of G that contains a must contain H: Let S be the set of all positive n such that an ...
Math 3121 Abstract Algebra I
... is a subgroup of G and is the smallest subgroup of G that contains a. Proof: See the book. Sketch: H satisfies the three properties for subgroups on the previous theorem. Thus is a subgroup. To prove any subgroup K of G that contains a must contain H: Let S be the set of all positive n such that an ...
... is a subgroup of G and is the smallest subgroup of G that contains a. Proof: See the book. Sketch: H satisfies the three properties for subgroups on the previous theorem. Thus is a subgroup. To prove any subgroup K of G that contains a must contain H: Let S be the set of all positive n such that an ...
GROUPS WITH FEW CONJUGACY CLASSES 1. Introduction
... then k(G) ≥ 2 p − 1. Finally Keller [6] showed that√there exists a universal positive constant C so that whenever p > C then k(G) ≥ 2 p − 1 for any finite group G. In this paper we extend these results to show Theorem 1.1. By disregarding at most finitely many non-solvable p-solvable groups ...
... then k(G) ≥ 2 p − 1. Finally Keller [6] showed that√there exists a universal positive constant C so that whenever p > C then k(G) ≥ 2 p − 1 for any finite group G. In this paper we extend these results to show Theorem 1.1. By disregarding at most finitely many non-solvable p-solvable groups ...
15. Isomorphisms (continued) We start by recalling the notions of an
... Doing this directly from definition is usually impossible (one cannot go over all possible maps between groups and show directly that none of them can be both bijective and operation-preserving). Of course, two groups cannot be isomorphic if they have different orders. If two groups G and G0 have th ...
... Doing this directly from definition is usually impossible (one cannot go over all possible maps between groups and show directly that none of them can be both bijective and operation-preserving). Of course, two groups cannot be isomorphic if they have different orders. If two groups G and G0 have th ...
12. Subgroups Definition. Let (G,∗) be a group. A subset H of G is
... (ii) Take any g, h ∈ C(a). This means that ga = ag and ha = ah. We need to use these equalities to show that gh ∈ C(a), that is, (gh)a = a(gh). The computation below proves this: (gh)a = g(ha) = g(ah) = (ga)h = (ag)h = a(gh) where the first, third and fifth equalities hold by associativity, the seco ...
... (ii) Take any g, h ∈ C(a). This means that ga = ag and ha = ah. We need to use these equalities to show that gh ∈ C(a), that is, (gh)a = a(gh). The computation below proves this: (gh)a = g(ha) = g(ah) = (ga)h = (ag)h = a(gh) where the first, third and fifth equalities hold by associativity, the seco ...
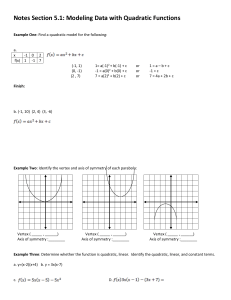
Notes Section 5.1: Modeling Data with Quadratic Functions Example
... Example: Solve using Factoring or the Quadratic Formula 3x2-x=4 ...
... Example: Solve using Factoring or the Quadratic Formula 3x2-x=4 ...
ON THE POPOV-POMMERENING CONJECTURE FOR GROUPS
... and (hence) all its conjugates are Grosshans subgroups of GL5(zc). Other subgroups of GL5(k) (n < 5) normalized by a maximal torus can be checked in the same spirit. (In fact, they can be proved to be Grosshans using various known results, cf. [G3], [Po2], [T], etc. [Po2] gives a more detailed accou ...
... and (hence) all its conjugates are Grosshans subgroups of GL5(zc). Other subgroups of GL5(k) (n < 5) normalized by a maximal torus can be checked in the same spirit. (In fact, they can be proved to be Grosshans using various known results, cf. [G3], [Po2], [T], etc. [Po2] gives a more detailed accou ...
FREE GROUPS - Stanford University
... resulting adjacent terms involving the same xj, and erasing identity elements if they occur. This perhaps seems somewhat more elementary and explicit than our previous construction of the free product of an arbitrary family of groups, but one has the same technical difficulties with associativity in ...
... resulting adjacent terms involving the same xj, and erasing identity elements if they occur. This perhaps seems somewhat more elementary and explicit than our previous construction of the free product of an arbitrary family of groups, but one has the same technical difficulties with associativity in ...
ABSTRACT ALGEBRA 1, LECTURE NOTES 5: HOMOMORPHISMS
... The idea behind an isomorphism of groups is that you may sometimes find yourself with two groups which aren’t literally equal, but there is a one-to-one correspondence between them which preserves the group operation, so they are “structured in the same way” as groups, but with the elements named di ...
... The idea behind an isomorphism of groups is that you may sometimes find yourself with two groups which aren’t literally equal, but there is a one-to-one correspondence between them which preserves the group operation, so they are “structured in the same way” as groups, but with the elements named di ...
Final with solutions
... Solution: We’ll first give a quick counting argument to find the answer. The center of the pendant is fixed under all symmetries, so it can be either a ruby or a sapphire. Whatever configuration of jewels on the vertices, it is easy to see that it is completely determined by the number of rubies: an ...
... Solution: We’ll first give a quick counting argument to find the answer. The center of the pendant is fixed under all symmetries, so it can be either a ruby or a sapphire. Whatever configuration of jewels on the vertices, it is easy to see that it is completely determined by the number of rubies: an ...
a ,b
... Rotation about an arbitrary axis through the origin can be decomposed into three basic rotations and hence, three matrix multiplications. The angles associated with each rotation are called the Euler angles. This seems very straightforward at first but suffers from a few drawbacks: computational ine ...
... Rotation about an arbitrary axis through the origin can be decomposed into three basic rotations and hence, three matrix multiplications. The angles associated with each rotation are called the Euler angles. This seems very straightforward at first but suffers from a few drawbacks: computational ine ...
THEOREM 1.1. Let G be a finite sovable group. Let two subgroups U
... In [2], it was shown that Losey-Stonehewer theorm holds without solvability. It is desired to generalize the theorem for infinite groups. In fact we have some generalizations for specific classes of locally finite groups[7]. In this note, we are concerned with profinite groups. 2. Profinite group An ...
... In [2], it was shown that Losey-Stonehewer theorm holds without solvability. It is desired to generalize the theorem for infinite groups. In fact we have some generalizations for specific classes of locally finite groups[7]. In this note, we are concerned with profinite groups. 2. Profinite group An ...