Cyclic Homology Theory, Part II
... where Un denotes the set of permutations with only one cycle, and A⊗• /1 − t is the Connes complex computing cyclic homology. 1. The algebra slr (k) is reductive, (glr (A)⊗n )Sn is an slr (k)-module, and we can consider the projection on the component corresponding to the trivial representation K ...
... where Un denotes the set of permutations with only one cycle, and A⊗• /1 − t is the Connes complex computing cyclic homology. 1. The algebra slr (k) is reductive, (glr (A)⊗n )Sn is an slr (k)-module, and we can consider the projection on the component corresponding to the trivial representation K ...
Full Text (PDF format)
... that the order of RJ21 RJ equals to the order of R21 R. But this is clear since they are conjugate. Corollary 3.4. Let H be a finite-dimensional Hopf algebra over k. Then exp(D(H)) = exp(H). Proof. By [RS], there exists J ∈ D(H) ⊗ D(H) such that D(D(H)) ∼ = (D(H) ⊗ D(H))J as Hopf algebras. Then using ...
... that the order of RJ21 RJ equals to the order of R21 R. But this is clear since they are conjugate. Corollary 3.4. Let H be a finite-dimensional Hopf algebra over k. Then exp(D(H)) = exp(H). Proof. By [RS], there exists J ∈ D(H) ⊗ D(H) such that D(D(H)) ∼ = (D(H) ⊗ D(H))J as Hopf algebras. Then using ...
WHAT DOES A LIE ALGEBRA KNOW ABOUT A LIE GROUP
... Lie groups provide a mathematical description of many naturally-occuring symmetries. Though they take a variety of shapes, Lie groups are closely linked to linear objects called Lie algebras. In fact, there is a direct correspondence between these two concepts: simply-connected Lie groups are isomor ...
... Lie groups provide a mathematical description of many naturally-occuring symmetries. Though they take a variety of shapes, Lie groups are closely linked to linear objects called Lie algebras. In fact, there is a direct correspondence between these two concepts: simply-connected Lie groups are isomor ...
B - Techtud
... Comparable: If A ⊆ B or B ⊆ A then A and B are comparable. 7. Proper subset: A set A is a subset of the set B but also A ≠ B, we write A ⊂ B and say that A is a proper subset of B i.e. A is a proper subset of B iff ∀x (x∈A → x∈B) ∧ ∃x (x∈B ∧ x∉A) 8. Finite set: A set in which number of elements are ...
... Comparable: If A ⊆ B or B ⊆ A then A and B are comparable. 7. Proper subset: A set A is a subset of the set B but also A ≠ B, we write A ⊂ B and say that A is a proper subset of B i.e. A is a proper subset of B iff ∀x (x∈A → x∈B) ∧ ∃x (x∈B ∧ x∉A) 8. Finite set: A set in which number of elements are ...
Universal enveloping algebra
... algebras. For this functor, f∗ = f for all F -algebra homomorphisms f : A → B. The reason that this works is elementary: f [a, b] = f (ab − ba) = f (a)f (b) − f (b)f (a) = [f (a), f (b)] ...
... algebras. For this functor, f∗ = f for all F -algebra homomorphisms f : A → B. The reason that this works is elementary: f [a, b] = f (ab − ba) = f (a)f (b) − f (b)f (a) = [f (a), f (b)] ...
Lie Algebra Cohomology
... Then A is a left g-module and x ◦ a is K-linear in x and a. Note also that by the universal property of U g the map ρ induces a unique algebra homomorphism ρ1 : U g → EndK A, thus making A in a left U gmodule. Conversely, if A is a left U g-module, so that we have a structure map σ : U g → EndK A, i ...
... Then A is a left g-module and x ◦ a is K-linear in x and a. Note also that by the universal property of U g the map ρ induces a unique algebra homomorphism ρ1 : U g → EndK A, thus making A in a left U gmodule. Conversely, if A is a left U g-module, so that we have a structure map σ : U g → EndK A, i ...
Lie Groups and Lie Algebras, Summer 2016
... Definition 2.1. A topological space is a set X with a collection of subsets T of X such that: 1. ∅ ∈ T and X ∈ T 2. if U1 , U2 ∈ T then U1 ∩ U2 ∈ T 3. if Ui ∈ T for all i in some index set I, then ∪i∈I Ui ∈ T The collection T is called the topology on X, and the elements in T are called the ”open se ...
... Definition 2.1. A topological space is a set X with a collection of subsets T of X such that: 1. ∅ ∈ T and X ∈ T 2. if U1 , U2 ∈ T then U1 ∩ U2 ∈ T 3. if Ui ∈ T for all i in some index set I, then ∪i∈I Ui ∈ T The collection T is called the topology on X, and the elements in T are called the ”open se ...
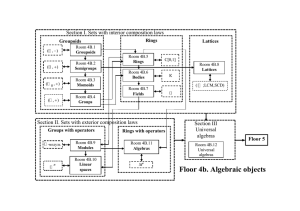
Section I. SETS WITH INTERIOR COMPOSITION LAWS
... Answer. This is the trivial group is the set with unique element е and operation , characterized by equality e e e . Example 4В.4 (task). Permutations group. Let М be a non empty finite set. The bijection from М to М is permutation. We determine an operation of superposition on the set Х of all ...
... Answer. This is the trivial group is the set with unique element е and operation , characterized by equality e e e . Example 4В.4 (task). Permutations group. Let М be a non empty finite set. The bijection from М to М is permutation. We determine an operation of superposition on the set Х of all ...