Chapter 2 Classical Models
... In this Chapter we will discuss models that can be described by classical statistical mechanics. We will concentrate on the classical spin models which are used not only to study magnetism but are valid also for other systems like binary alloys or lattice gases. In principle, all particles obey quan ...
... In this Chapter we will discuss models that can be described by classical statistical mechanics. We will concentrate on the classical spin models which are used not only to study magnetism but are valid also for other systems like binary alloys or lattice gases. In principle, all particles obey quan ...
The Stillinger-Weber Potential
... Different possible thermostats: Rescaling of velocities, Langevin-Andersen, Nosé-Hoover… more or less compatible with ensemble averages of statistical mechanics. ...
... Different possible thermostats: Rescaling of velocities, Langevin-Andersen, Nosé-Hoover… more or less compatible with ensemble averages of statistical mechanics. ...
Parallel Axis Theorem, Torque
... A ball rolls across the floor, and then starts up a ramp as shown below. In what direc6on does the angular accelera6on vector point when the ball is rolling back down the ramp? A) into the ...
... A ball rolls across the floor, and then starts up a ramp as shown below. In what direc6on does the angular accelera6on vector point when the ball is rolling back down the ramp? A) into the ...
V. Semiclassical theory of light-matter interactions Classical and
... which can be expressed in this manner by using any complete orthonormal set of state vectors. This form of the identity operator (which is also Hermitian) is very useful for finding series expansions for products of operators and vectors. ...
... which can be expressed in this manner by using any complete orthonormal set of state vectors. This form of the identity operator (which is also Hermitian) is very useful for finding series expansions for products of operators and vectors. ...
Equilibrium
... Big Idea: Consider qualitatively and quantitatively the characteristics and applications of equilibrium systems in chemical reactions What do you know about valence equilibrium? https://www.youtube.com/watch?v=dUMmoPdwBy4 ...
... Big Idea: Consider qualitatively and quantitatively the characteristics and applications of equilibrium systems in chemical reactions What do you know about valence equilibrium? https://www.youtube.com/watch?v=dUMmoPdwBy4 ...
Solutions for class #7 from Yosumism website Problem 44:
... One can derive the frequency of small oscillation for a rigid body in general by using the torque form of Newton's Laws: . (I is moment of inertia, r is moment arm) In this case, one has a constant downwards force , which acts at a moment arm angle . Thus, , where the approximation works if ...
... One can derive the frequency of small oscillation for a rigid body in general by using the torque form of Newton's Laws: . (I is moment of inertia, r is moment arm) In this case, one has a constant downwards force , which acts at a moment arm angle . Thus, , where the approximation works if ...
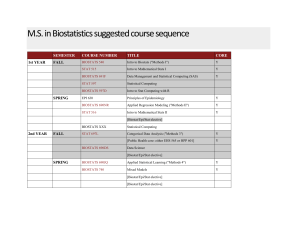
M.S. in Biostatistics suggested course sequence
... M.S. in Biostatistics suggested course sequence 1st YEAR ...
... M.S. in Biostatistics suggested course sequence 1st YEAR ...
Weighted Ensemble Simulations of Protein Dynamics
... • (e.g.) allosteric transitions take ms, but are composed of processes that take ps – ns. • Random nature of molecular motion results in a two-stepsforward-one-step-back kind of progress. • If we can focus our computing power on forward steps, we can improve the efficacy of calculation by orders ...
... • (e.g.) allosteric transitions take ms, but are composed of processes that take ps – ns. • Random nature of molecular motion results in a two-stepsforward-one-step-back kind of progress. • If we can focus our computing power on forward steps, we can improve the efficacy of calculation by orders ...
Equilibrium of a Particle
... Best representation of all the unknown forces (∑F) which acts on a body A sketch showing the particle “free” from the surroundings with all the forces acting on it Consider two common connections in this subject – Spring Cables and Pulleys ...
... Best representation of all the unknown forces (∑F) which acts on a body A sketch showing the particle “free” from the surroundings with all the forces acting on it Consider two common connections in this subject – Spring Cables and Pulleys ...
Copenhagen Interpretation
... If this works, then Quantum Mechanics is incomplete, that is, it’s actually possible to make precise measurements if we’re clever, and there’s more going on than is in Quantum Mechanics. ...
... If this works, then Quantum Mechanics is incomplete, that is, it’s actually possible to make precise measurements if we’re clever, and there’s more going on than is in Quantum Mechanics. ...
Statistical Physics
... MODULE RATIONALE: In this section you will get the answer to questions like “Why should I study this module as pre-service teacher trainee? What is its relevance to my career?” ...
... MODULE RATIONALE: In this section you will get the answer to questions like “Why should I study this module as pre-service teacher trainee? What is its relevance to my career?” ...
The Concept of Statistical Significance Testing.
... Researchers may invoke statistical significance testing whenever they have a random sample from a population, or a sample that they believe approximates a random, representative sample. Statistical significance testing requires subjective judgment in setting a predetermined acceptable probability (r ...
... Researchers may invoke statistical significance testing whenever they have a random sample from a population, or a sample that they believe approximates a random, representative sample. Statistical significance testing requires subjective judgment in setting a predetermined acceptable probability (r ...
SENIOR SIX MATHS SEMINAR
... a) By using a suitable table of values show that the equation x3 – 3x + 1 = 0 has three roots in the interval (2, 2). Use linear interpolation once to find the negative root of the equation. (b) Using the trapezium rule with 5 ordinate values, estimate the value of to 4d.p. ...
... a) By using a suitable table of values show that the equation x3 – 3x + 1 = 0 has three roots in the interval (2, 2). Use linear interpolation once to find the negative root of the equation. (b) Using the trapezium rule with 5 ordinate values, estimate the value of to 4d.p. ...