Lecture 1
... The history of optical theories shows that the scientific view has for long oscillated between a mechanical and an undulatory conception of light; however, these two views are perhaps less opposed to one another than was previously thought, and the development of quantum theory, in particular, appea ...
... The history of optical theories shows that the scientific view has for long oscillated between a mechanical and an undulatory conception of light; however, these two views are perhaps less opposed to one another than was previously thought, and the development of quantum theory, in particular, appea ...
Modern physics 2330
... 2- ( ) An event is determined by the location where, and by the time at which occurs. 3- ( ) According to classical mechanics, a moving clock runs slower than one at rest. 4- ( ) The number, strength, and exact position of the lines in the spectrum of an element depend only upon temperature. 5- ( ) ...
... 2- ( ) An event is determined by the location where, and by the time at which occurs. 3- ( ) According to classical mechanics, a moving clock runs slower than one at rest. 4- ( ) The number, strength, and exact position of the lines in the spectrum of an element depend only upon temperature. 5- ( ) ...
Problem 1. Domain walls of ϕ theory. [10 pts]
... The boundary condition is chosen so as to force the domain wall solution ϕ(x) interpolating between ±ϕ1 values at the boundaries. From now on we assume that everything is uniform along y-axis and consider the Lagrangian corresponding to SLG as y-independent. ...
... The boundary condition is chosen so as to force the domain wall solution ϕ(x) interpolating between ±ϕ1 values at the boundaries. From now on we assume that everything is uniform along y-axis and consider the Lagrangian corresponding to SLG as y-independent. ...
PHYS 305 - Modern Physics (Spring 2016) Department of Physics
... Modern Physics is a undergraduate level course which is intended for students, who have already studied introductory level physics. This course provides a basic introduction to better understanding of special relativity, Quantum mechanics, and applications of quantum theory to: atomic and molecular ...
... Modern Physics is a undergraduate level course which is intended for students, who have already studied introductory level physics. This course provides a basic introduction to better understanding of special relativity, Quantum mechanics, and applications of quantum theory to: atomic and molecular ...
LOYOLA COLLEGE (AUTONOMOUS), CHENNAI – 600 034
... 11. What is a hermitian operator? Show that the wave functions corresponding to two different eigen values of a Hermitian operator are orthogonal. 12. The high temperature microwave spectrum of KCl vapor shows an absorption at 7687.94 MHz that can be identified with J=0 to J=1 transition of 39K35Cl ...
... 11. What is a hermitian operator? Show that the wave functions corresponding to two different eigen values of a Hermitian operator are orthogonal. 12. The high temperature microwave spectrum of KCl vapor shows an absorption at 7687.94 MHz that can be identified with J=0 to J=1 transition of 39K35Cl ...
Journey into the Microcosm – The Story of Elementary Particles
... 208) is a trifle unfortunate, since the term ‘ghosts’ is used for other quantum fields which appear in the quantization of gauge theories. These examples are only indicative and certainly not exhaustive. There are quite a few more. Perhaps, they can be corrected in future editions and more care will ...
... 208) is a trifle unfortunate, since the term ‘ghosts’ is used for other quantum fields which appear in the quantization of gauge theories. These examples are only indicative and certainly not exhaustive. There are quite a few more. Perhaps, they can be corrected in future editions and more care will ...
•Course: Introduction to Green functions in Physics •Lecturer: Mauro Ferreira •Recommended Bibliography:
... If f(z) has a pole of order n at z=z0, to find the residue we multiply f(z) by (z-z0)n, differentiate the result (n-1) times, divide it by (n-1)! and evaluate the result at z=z0. ...
... If f(z) has a pole of order n at z=z0, to find the residue we multiply f(z) by (z-z0)n, differentiate the result (n-1) times, divide it by (n-1)! and evaluate the result at z=z0. ...
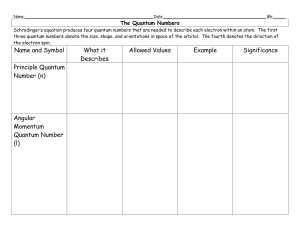
e-the-quantum-numberssv-2
... The Quantum Numbers Schrodinger’s equation produces four quantum numbers that are needed to describe each electron within an atom. The first three quantum numbers denote the size, shape, and orientations in space of the orbital. The fourth denotes the direction of the electron spin. ...
... The Quantum Numbers Schrodinger’s equation produces four quantum numbers that are needed to describe each electron within an atom. The first three quantum numbers denote the size, shape, and orientations in space of the orbital. The fourth denotes the direction of the electron spin. ...
PHY4605–Introduction to Quantum Mechanics II Spring 1997 Problem Set 4 Jan. 31, 2005
... point-proton model to be δV (r) = V1 (r) − V0 (r). Use 1st-order perturbation theory to find the correction δE0 to the ground state energy due to the finite size of the proton. Obtain a numerical value for the fractional correction δE0 /E0 . (Hint: you can simplify the calculation by noting that r0 ...
... point-proton model to be δV (r) = V1 (r) − V0 (r). Use 1st-order perturbation theory to find the correction δE0 to the ground state energy due to the finite size of the proton. Obtain a numerical value for the fractional correction δE0 /E0 . (Hint: you can simplify the calculation by noting that r0 ...
QUASICLASSICAL AND QUANTUM SYSTEMS OF ANGULAR FOR QUANTUM-MECHANICAL MODELS WITH SYMMETRIES
... for describing certain problems concerning the quantum dynamics of systems of angular momenta, including also the spin systems. The underlying groups are SU(2) and its quotient SO(3, R). The proposed scheme is applied in two different contexts. Firstly, the purely group-algebraic framework is applie ...
... for describing certain problems concerning the quantum dynamics of systems of angular momenta, including also the spin systems. The underlying groups are SU(2) and its quotient SO(3, R). The proposed scheme is applied in two different contexts. Firstly, the purely group-algebraic framework is applie ...
LOYOLA COLLEGE (AUTONOMOUS), CHENNAI
... potential V(x) = 0 for –a < x < a and V(x) = ∞ for │x│ > a. (b) An electron in one dimensional infinite potential well goes from n = 4 to n =2, the frequency of the emitted photon is 3.43 x 1014 Hz. Find the width of the path. ...
... potential V(x) = 0 for –a < x < a and V(x) = ∞ for │x│ > a. (b) An electron in one dimensional infinite potential well goes from n = 4 to n =2, the frequency of the emitted photon is 3.43 x 1014 Hz. Find the width of the path. ...
Tutorial 7
... Energy of the transition from the first energy level to the third energy level in a hydrogen atom. ...
... Energy of the transition from the first energy level to the third energy level in a hydrogen atom. ...
Renormalization group

In theoretical physics, the renormalization group (RG) refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales. In particle physics, it reflects the changes in the underlying force laws (codified in a quantum field theory) as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle (cf. Compton wavelength).A change in scale is called a ""scale transformation"". The renormalization group is intimately related to ""scale invariance"" and ""conformal invariance"", symmetries in which a system appears the same at all scales (so-called self-similarity). (However, note that scale transformations are included in conformal transformations, in general: the latter including additional symmetry generators associated with special conformal transformations.)As the scale varies, it is as if one is changing the magnifying power of a notional microscope viewing the system. In so-called renormalizable theories, the system at one scale will generally be seen to consist of self-similar copies of itself when viewed at a smaller scale, with different parameters describing the components of the system. The components, or fundamental variables, may relate to atoms, elementary particles, atomic spins, etc. The parameters of the theory typically describe the interactions of the components. These may be variable ""couplings"" which measure the strength of various forces, or mass parameters themselves. The components themselves may appear to be composed of more of the self-same components as one goes to shorter distances.For example, in quantum electrodynamics (QED), an electron appears to be composed of electrons, positrons (anti-electrons) and photons, as one views it at higher resolution, at very short distances. The electron at such short distances has a slightly different electric charge than does the ""dressed electron"" seen at large distances, and this change, or ""running,"" in the value of the electric charge is determined by the renormalization group equation.



![Problem 1. Domain walls of ϕ theory. [10 pts]](http://s1.studyres.com/store/data/008941810_1-60c5d1d637847e1c41f4f005f4c29c0f-300x300.png)