Lecture 12 Atomic structure
... Before embarking on this programme, we should first consider our ambitions: The development of computation schemes to address quantum mechanics of many-particle systems is a specialist (and challenging) topic common to physics and chemistry. Our interest here is merely in the outcome of such investi ...
... Before embarking on this programme, we should first consider our ambitions: The development of computation schemes to address quantum mechanics of many-particle systems is a specialist (and challenging) topic common to physics and chemistry. Our interest here is merely in the outcome of such investi ...
File - Score Booster Project
... • Orientation of the orbitals in space is described by this quantum number • The value of m depends on the value of l (m = -I to +l) • E.g. if l =1, m = -1, 0, +1 • This means that there are 3 different p-subshells for a particular orbital. These subshells have the same energy but different orientat ...
... • Orientation of the orbitals in space is described by this quantum number • The value of m depends on the value of l (m = -I to +l) • E.g. if l =1, m = -1, 0, +1 • This means that there are 3 different p-subshells for a particular orbital. These subshells have the same energy but different orientat ...
HW #5
... 4. A right triangular wedge of mass M and angle θ rests on a horizontal table. A block of mass m rests on the wedge. The contacts between wedge and table and between wedge and block are frictionless. a. What horizontal acceleration must the wedge have relative to the table so that the block stays st ...
... 4. A right triangular wedge of mass M and angle θ rests on a horizontal table. A block of mass m rests on the wedge. The contacts between wedge and table and between wedge and block are frictionless. a. What horizontal acceleration must the wedge have relative to the table so that the block stays st ...
Potential Energy - McMaster Physics and Astronomy
... One useful result: for elastic collisions, the magnitude of the relative velocity is the same before and after the collision: |v1,i – v2,i | = |v1,f – v2,f | (This is true for elastic collisions in 2 and 3 dimensions as well). An important case is a particle directed at a stationary target (v2,i = ...
... One useful result: for elastic collisions, the magnitude of the relative velocity is the same before and after the collision: |v1,i – v2,i | = |v1,f – v2,f | (This is true for elastic collisions in 2 and 3 dimensions as well). An important case is a particle directed at a stationary target (v2,i = ...
Uncertainty Principle
... was awarded nobel prize in physics in 1954. He said, the probability of finding a particle in an elementary volume element dv around a point ~r in theR space is given by dp = ΨΨ∗ dv. The probability finding it in a volume area V is given by p = V ΨΨ∗ dv. Since the particle must be somewhere in the a ...
... was awarded nobel prize in physics in 1954. He said, the probability of finding a particle in an elementary volume element dv around a point ~r in theR space is given by dp = ΨΨ∗ dv. The probability finding it in a volume area V is given by p = V ΨΨ∗ dv. Since the particle must be somewhere in the a ...
Van Wezel_DEF.indd
... in a measurable prediction that could validate or falsify the theory. There is however one recent idea due to Roger Penrose who suggested that general relativity could cause spatial quantum superpositions to become unstable [26, 27]. Based on some very general arguments, Penrose showed that this gra ...
... in a measurable prediction that could validate or falsify the theory. There is however one recent idea due to Roger Penrose who suggested that general relativity could cause spatial quantum superpositions to become unstable [26, 27]. Based on some very general arguments, Penrose showed that this gra ...
...detail
... current density and equation of continuity; potential difference and electromotive force, electric energy sources – voltage source and current source; metallic conduction and Ohm’s law, conductance and resistance as parameters; circuit elements, passive an active, linear and nonlinear, analysis of r ...
... current density and equation of continuity; potential difference and electromotive force, electric energy sources – voltage source and current source; metallic conduction and Ohm’s law, conductance and resistance as parameters; circuit elements, passive an active, linear and nonlinear, analysis of r ...
The Future of Computer Science
... Relativity and the Second Law respectively So what about the third one? What are the ultimate physical limits on what can be feasibly computed? And do those limits have any implications for physics? ...
... Relativity and the Second Law respectively So what about the third one? What are the ultimate physical limits on what can be feasibly computed? And do those limits have any implications for physics? ...
Physics 564 - Fall 2005, Assignment #1
... 9. Using the experimental resolutions on the momentum measurements in the transverse and longitudinal directions to smear the calculated momenta of the K − and π + . Then fill a histogram with the measured invariant mass of the K − π + pair. 10. As described above, a pion is incorrectly identified ...
... 9. Using the experimental resolutions on the momentum measurements in the transverse and longitudinal directions to smear the calculated momenta of the K − and π + . Then fill a histogram with the measured invariant mass of the K − π + pair. 10. As described above, a pion is incorrectly identified ...
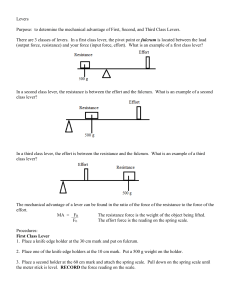
Levers Lab
... 4. Move the spring scale and holder to the 80 cm mark. Pull down on the spring scale until the meter stick is level. RECORD the force reading on the scale. 5. Move the spring scale and holder to the 100 cm mark (or as close as you can get it). Pull down on the spring scale until the meter stick is ...
... 4. Move the spring scale and holder to the 80 cm mark. Pull down on the spring scale until the meter stick is level. RECORD the force reading on the scale. 5. Move the spring scale and holder to the 100 cm mark (or as close as you can get it). Pull down on the spring scale until the meter stick is ...
Renormalization group

In theoretical physics, the renormalization group (RG) refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales. In particle physics, it reflects the changes in the underlying force laws (codified in a quantum field theory) as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle (cf. Compton wavelength).A change in scale is called a ""scale transformation"". The renormalization group is intimately related to ""scale invariance"" and ""conformal invariance"", symmetries in which a system appears the same at all scales (so-called self-similarity). (However, note that scale transformations are included in conformal transformations, in general: the latter including additional symmetry generators associated with special conformal transformations.)As the scale varies, it is as if one is changing the magnifying power of a notional microscope viewing the system. In so-called renormalizable theories, the system at one scale will generally be seen to consist of self-similar copies of itself when viewed at a smaller scale, with different parameters describing the components of the system. The components, or fundamental variables, may relate to atoms, elementary particles, atomic spins, etc. The parameters of the theory typically describe the interactions of the components. These may be variable ""couplings"" which measure the strength of various forces, or mass parameters themselves. The components themselves may appear to be composed of more of the self-same components as one goes to shorter distances.For example, in quantum electrodynamics (QED), an electron appears to be composed of electrons, positrons (anti-electrons) and photons, as one views it at higher resolution, at very short distances. The electron at such short distances has a slightly different electric charge than does the ""dressed electron"" seen at large distances, and this change, or ""running,"" in the value of the electric charge is determined by the renormalization group equation.