Purdue Physics - Purdue University
... l ti arise i b because th the cars exert internal forces on each other. • Momentum conservation allows us to determine the change in velocity without knowing what the internal forces are. • Note that often momentum is conserved but the kinetic energy is not! (Kinetic energy is conserved only in elas ...
... l ti arise i b because th the cars exert internal forces on each other. • Momentum conservation allows us to determine the change in velocity without knowing what the internal forces are. • Note that often momentum is conserved but the kinetic energy is not! (Kinetic energy is conserved only in elas ...
Structural( biology( at( the( single( particle( level:( imaging( tobacco
... products. It addresses some of the unsolved questions of modern science: the nature of the fundamental forces and underlying symmetries, as well as the nature of the gravitational force at very small distances. New facilities and technological developments now open the window for significant improve ...
... products. It addresses some of the unsolved questions of modern science: the nature of the fundamental forces and underlying symmetries, as well as the nature of the gravitational force at very small distances. New facilities and technological developments now open the window for significant improve ...
Spin Azimuthal Asymmetries inSemi-Inclusive DIS at
... Key goal: study the transition between the nonperturbative and perturbative regimes of QCD utilizing JLab’s advantages: High luminosity Full coverage in azimuthal angle (separate all contributions) Wide kinematic range (test factorization, measure HT) Good particle ID (compare different final st ...
... Key goal: study the transition between the nonperturbative and perturbative regimes of QCD utilizing JLab’s advantages: High luminosity Full coverage in azimuthal angle (separate all contributions) Wide kinematic range (test factorization, measure HT) Good particle ID (compare different final st ...
UNITARY OPERATORS AND SYMMETRY TRANSFORMATIONS
... state, either |α and |β , use a measurement to guess which one. If |α and |β are not orthogonal, then no measurement perfectly distinguishes them, and we always have some constant probability of error. However, if we could make many copies of the unknown state, then we could repeat the optimal measu ...
... state, either |α and |β , use a measurement to guess which one. If |α and |β are not orthogonal, then no measurement perfectly distinguishes them, and we always have some constant probability of error. However, if we could make many copies of the unknown state, then we could repeat the optimal measu ...
Chapter 9: Momentum and Conservation
... Angular Momentum Just like linear momentum is mv, a ROTATING object has momentum also. The momentum of a rotating object is called Angular Momentum and depends on the object’s mass, distance from the center axis of rotation, and tangential velocity. If the radius gets smaller, the velocity increase ...
... Angular Momentum Just like linear momentum is mv, a ROTATING object has momentum also. The momentum of a rotating object is called Angular Momentum and depends on the object’s mass, distance from the center axis of rotation, and tangential velocity. If the radius gets smaller, the velocity increase ...
Full Text - International Press of Boston
... In particular, n1 = 1, n2 = 1, n3 = 12. This recursion formula for computing nd for CP2 was first derived by Kontsevich, using the composition law previously predicted by physicists and now proved in our paper [RT]. We can also compute the degree of the moduli space of genus g curves in CPn by using ...
... In particular, n1 = 1, n2 = 1, n3 = 12. This recursion formula for computing nd for CP2 was first derived by Kontsevich, using the composition law previously predicted by physicists and now proved in our paper [RT]. We can also compute the degree of the moduli space of genus g curves in CPn by using ...
1 - vnhsteachers
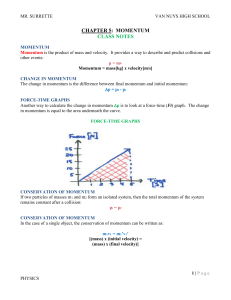
... Momentum is the product of mass and velocity. It provides a way to describe and predict collisions and other events: p = mv Momentum = mass[kg] x velocity[m/s] CHANGE IN MOMENTUM The change in momentum is the difference between final momentum and initial momentum: p = pf - pi FORCE-TIME GRAPHS Anot ...
... Momentum is the product of mass and velocity. It provides a way to describe and predict collisions and other events: p = mv Momentum = mass[kg] x velocity[m/s] CHANGE IN MOMENTUM The change in momentum is the difference between final momentum and initial momentum: p = pf - pi FORCE-TIME GRAPHS Anot ...
ValenciaHiesmayr2008
... Bell inequality sensitive to strangeness violated? Can we violate the BI for a certain initial state and if, what is the maximum value? Hiesmayr, Eur. Phys. J. C (2007) ...
... Bell inequality sensitive to strangeness violated? Can we violate the BI for a certain initial state and if, what is the maximum value? Hiesmayr, Eur. Phys. J. C (2007) ...
Nobel Prize in Physics 2016 Flatland and Topology
... of the system; on each edge, these modes move in only one direction So even if there is an impurity at the edge, the modes do not get reflected back but continue to move in the same direction ...
... of the system; on each edge, these modes move in only one direction So even if there is an impurity at the edge, the modes do not get reflected back but continue to move in the same direction ...
The Family Problem: Extension of Standard Model with a Loosely
... “family” Higgs mechanism via spontaneous symmetry breaking, while the remaining four become massive Higgs particles. (In the previous application, it was referred to as “colored Higgs Mechanism”[1].) ...
... “family” Higgs mechanism via spontaneous symmetry breaking, while the remaining four become massive Higgs particles. (In the previous application, it was referred to as “colored Higgs Mechanism”[1].) ...
Quantum - Caltech Particle Theory
... “where can the`lens’ provided by theoretical CS be a useful tool in other fields?” What can the study of quantum computation and quantum information tell us about physics? ...
... “where can the`lens’ provided by theoretical CS be a useful tool in other fields?” What can the study of quantum computation and quantum information tell us about physics? ...
Renormalization group

In theoretical physics, the renormalization group (RG) refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales. In particle physics, it reflects the changes in the underlying force laws (codified in a quantum field theory) as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle (cf. Compton wavelength).A change in scale is called a ""scale transformation"". The renormalization group is intimately related to ""scale invariance"" and ""conformal invariance"", symmetries in which a system appears the same at all scales (so-called self-similarity). (However, note that scale transformations are included in conformal transformations, in general: the latter including additional symmetry generators associated with special conformal transformations.)As the scale varies, it is as if one is changing the magnifying power of a notional microscope viewing the system. In so-called renormalizable theories, the system at one scale will generally be seen to consist of self-similar copies of itself when viewed at a smaller scale, with different parameters describing the components of the system. The components, or fundamental variables, may relate to atoms, elementary particles, atomic spins, etc. The parameters of the theory typically describe the interactions of the components. These may be variable ""couplings"" which measure the strength of various forces, or mass parameters themselves. The components themselves may appear to be composed of more of the self-same components as one goes to shorter distances.For example, in quantum electrodynamics (QED), an electron appears to be composed of electrons, positrons (anti-electrons) and photons, as one views it at higher resolution, at very short distances. The electron at such short distances has a slightly different electric charge than does the ""dressed electron"" seen at large distances, and this change, or ""running,"" in the value of the electric charge is determined by the renormalization group equation.