SECTION 10.3 LECTURE NOTES
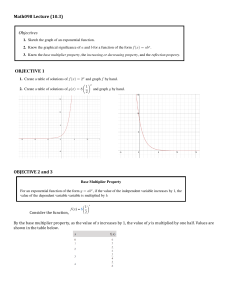
... 3. Find x when f(x) = 0. Ans: there is no value of x where f(x) = 0. Because the graph of an exponential functions gets close to, but never r ...
... 3. Find x when f(x) = 0. Ans: there is no value of x where f(x) = 0. Because the graph of an exponential functions gets close to, but never r ...
talk
... This would be a local theory with hidden variables, and quantum mechanics might be considered as an averaged version of the deeper theory. Analogy: Statistical thermodynamics is the underlying theory of phenomenological thermodynamics. The positions and momenta of a huge number of particles are the ...
... This would be a local theory with hidden variables, and quantum mechanics might be considered as an averaged version of the deeper theory. Analogy: Statistical thermodynamics is the underlying theory of phenomenological thermodynamics. The positions and momenta of a huge number of particles are the ...
Coherence of atomic matter-wave fields - IAP TU
... In analogy to Glauber’s analysis of optical coherence @1#, we adopt an operational approach where different classes of atomic coherence are associated with different types of measurements. For the sake of concreteness we consider specifically three classes of measurements: fluorescence, nonresonant ...
... In analogy to Glauber’s analysis of optical coherence @1#, we adopt an operational approach where different classes of atomic coherence are associated with different types of measurements. For the sake of concreteness we consider specifically three classes of measurements: fluorescence, nonresonant ...
Physics at NICA , the view from LPI RAS
... • Remarks on “elementary” particle source its generalization on high density case. • Rescattering of “elementary” sources and transverse and longitudinal spectra in pA and AB collisions. • Event-by-event fluctuations of transverse momenta Is the produced dense strongly interacting matter homogeneous ...
... • Remarks on “elementary” particle source its generalization on high density case. • Rescattering of “elementary” sources and transverse and longitudinal spectra in pA and AB collisions. • Event-by-event fluctuations of transverse momenta Is the produced dense strongly interacting matter homogeneous ...
Mesoscopic Effects in the Fractional Quantum Hall Regime: Chiral Luttinger... versus Fermi Liquid
... However, the nonlocal terms scale in the same way as the local terms. The Kane-Fisher flow equations are therefore valid in the antidot problem considered here. This scaling analysis shows that off resonance [22] and at low enough temperatures the antidot will be in the strongly coupled regime shown ...
... However, the nonlocal terms scale in the same way as the local terms. The Kane-Fisher flow equations are therefore valid in the antidot problem considered here. This scaling analysis shows that off resonance [22] and at low enough temperatures the antidot will be in the strongly coupled regime shown ...
np W. L. Glab and P. T. Glynn F. Robicheaux
... previously for several systems, including the np Rydberg states of molecular hydrogen @13,14#, although in that case the transformation is from Hund’s case ~b! to Hund’s case ~d! angular momentum coupling. Rather than this phenomenological approach, for this study we chose to compare the experimenta ...
... previously for several systems, including the np Rydberg states of molecular hydrogen @13,14#, although in that case the transformation is from Hund’s case ~b! to Hund’s case ~d! angular momentum coupling. Rather than this phenomenological approach, for this study we chose to compare the experimenta ...
Geometric Entropy of Self-Gravitating Systems
... turn based on a semiclassical approximation of Quantum Mechanics on a curved background, or some equivalent classical result about Geodesics Geometry (see [20]). The further identifications between the temperature and other geometrical entities (surface gravity of the horizon [3], the period of time ...
... turn based on a semiclassical approximation of Quantum Mechanics on a curved background, or some equivalent classical result about Geodesics Geometry (see [20]). The further identifications between the temperature and other geometrical entities (surface gravity of the horizon [3], the period of time ...
Emergent quasicrystals in strongly correlated systems
... further demonstrated experimentally that similar effects stabilize incommensurate composite crystals [24–26]. Related effects appear also in quantum systems, e.g., the frustration between the lattice and magnetic length scales in the Hofstadter problem [27] gives rise to a fractal spectrum [28]. As ...
... further demonstrated experimentally that similar effects stabilize incommensurate composite crystals [24–26]. Related effects appear also in quantum systems, e.g., the frustration between the lattice and magnetic length scales in the Hofstadter problem [27] gives rise to a fractal spectrum [28]. As ...
Standard and derived Planck quantities
... These are the three basic Planck units; they serve as the basis not only for many other possible Planck quantities, but more importantly, they set the scale for quantum gravity phenomena. As we will discuss here, there are many analogs to these units for other physical quantities, as well. We will ...
... These are the three basic Planck units; they serve as the basis not only for many other possible Planck quantities, but more importantly, they set the scale for quantum gravity phenomena. As we will discuss here, there are many analogs to these units for other physical quantities, as well. We will ...
Electromagnetic radiation and resonance
... structure or at least one could estimate their size. In the matter of the photon, not only do any conjectures as to its structure lack but even there are no reasonable guesses about its dimensions. In this connection it should be remarked that the dual (particle-like and wavelike) properties of an o ...
... structure or at least one could estimate their size. In the matter of the photon, not only do any conjectures as to its structure lack but even there are no reasonable guesses about its dimensions. In this connection it should be remarked that the dual (particle-like and wavelike) properties of an o ...
Document
... to x the number f ′(x). So we can regard f ′ as a new function, called the derivative of f and defined by Equation 2. We know that the value of f ′ at x, f ′(x), can be interpreted geometrically as the slope of the tangent line to the graph of f at the point (x, f (x)). The function f ′ is called th ...
... to x the number f ′(x). So we can regard f ′ as a new function, called the derivative of f and defined by Equation 2. We know that the value of f ′ at x, f ′(x), can be interpreted geometrically as the slope of the tangent line to the graph of f at the point (x, f (x)). The function f ′ is called th ...
Renormalization group

In theoretical physics, the renormalization group (RG) refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales. In particle physics, it reflects the changes in the underlying force laws (codified in a quantum field theory) as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle (cf. Compton wavelength).A change in scale is called a ""scale transformation"". The renormalization group is intimately related to ""scale invariance"" and ""conformal invariance"", symmetries in which a system appears the same at all scales (so-called self-similarity). (However, note that scale transformations are included in conformal transformations, in general: the latter including additional symmetry generators associated with special conformal transformations.)As the scale varies, it is as if one is changing the magnifying power of a notional microscope viewing the system. In so-called renormalizable theories, the system at one scale will generally be seen to consist of self-similar copies of itself when viewed at a smaller scale, with different parameters describing the components of the system. The components, or fundamental variables, may relate to atoms, elementary particles, atomic spins, etc. The parameters of the theory typically describe the interactions of the components. These may be variable ""couplings"" which measure the strength of various forces, or mass parameters themselves. The components themselves may appear to be composed of more of the self-same components as one goes to shorter distances.For example, in quantum electrodynamics (QED), an electron appears to be composed of electrons, positrons (anti-electrons) and photons, as one views it at higher resolution, at very short distances. The electron at such short distances has a slightly different electric charge than does the ""dressed electron"" seen at large distances, and this change, or ""running,"" in the value of the electric charge is determined by the renormalization group equation.























