MATH M25A - Moorpark College
... Use differentials with linear approximation problems. (optional*) Find an approximate solution to an equation using Newton’s Method. (optional*) Apply the basic rules of integration for finding anti-derivatives for algebraic and transcendental functions. Use summation notation with Riemann sums and ...
... Use differentials with linear approximation problems. (optional*) Find an approximate solution to an equation using Newton’s Method. (optional*) Apply the basic rules of integration for finding anti-derivatives for algebraic and transcendental functions. Use summation notation with Riemann sums and ...
![The Fundamental Theorem of Calculus [1]](http://s1.studyres.com/store/data/020099492_1-4a7fbd2304ff84025ef2f0bc4ff924ca-300x300.png)
The Fundamental Theorem of Calculus [1]
... Remark 2.3 Using Leibniz notion for derivatives, we can write FTC1 as ∫ x d f (t)dt = f (x) dx a ...
... Remark 2.3 Using Leibniz notion for derivatives, we can write FTC1 as ∫ x d f (t)dt = f (x) dx a ...
Course Code
... Mathematics is an universal language. Because of this, building a mathematical model to solve a problem in any field is crucial. Then our purpose is giving not only basic mathematical knowledge and mathematical idea but also the technique of the solving a problem. Matrices: Definition, Null matrix, ...
... Mathematics is an universal language. Because of this, building a mathematical model to solve a problem in any field is crucial. Then our purpose is giving not only basic mathematical knowledge and mathematical idea but also the technique of the solving a problem. Matrices: Definition, Null matrix, ...
A quick review of Mathe 114
... Final sketching: (i). Locate a few special points: points on the x-/y- axes; local maximum/minimum value points (ii). Divide the domain of the function into many subintervals by the critical points, inflection points and those points where the function is not defined; (iii). Indicate if f is increas ...
... Final sketching: (i). Locate a few special points: points on the x-/y- axes; local maximum/minimum value points (ii). Divide the domain of the function into many subintervals by the critical points, inflection points and those points where the function is not defined; (iii). Indicate if f is increas ...
Calculus Jeopardy - Designated Deriver
... calculations of area using anti-derivatives. What is The Fundamental Theorem of Calculus? ...
... calculations of area using anti-derivatives. What is The Fundamental Theorem of Calculus? ...
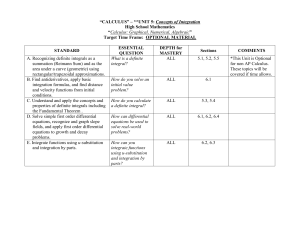
Unit 5
... C. Understand and apply the concepts and properties of definite integrals including the Fundamental Theorem . D. Solve simple first order differential equations, recognize and graph slope fields, and apply first order differential equations to growth and decay problems. E. Integrate functions using ...
... C. Understand and apply the concepts and properties of definite integrals including the Fundamental Theorem . D. Solve simple first order differential equations, recognize and graph slope fields, and apply first order differential equations to growth and decay problems. E. Integrate functions using ...
2015_Spring_M140_TopicsList
... Integrals of polynomials and trig functions, using substitution if necessary -- Chapter 4 Review / 9-24 Integrals that involve ex or ln(x), using substitution if necessary -- 6.2 / 79-90, 6.4 / 71-80 Finding an antiderivative that satisfies an extra condition -- 3.9 / 27-32 Estimation of an integral ...
... Integrals of polynomials and trig functions, using substitution if necessary -- Chapter 4 Review / 9-24 Integrals that involve ex or ln(x), using substitution if necessary -- 6.2 / 79-90, 6.4 / 71-80 Finding an antiderivative that satisfies an extra condition -- 3.9 / 27-32 Estimation of an integral ...
Lebesgue integration
In mathematics, the integral of a non-negative function can be regarded, in the simplest case, as the area between the graph of that function and the x-axis. The Lebesgue integral extends the integral to a larger class of functions. It also extends the domains on which these functions can be defined.Mathematicians had long understood that for non-negative functions with a smooth enough graph—such as continuous functions on closed bounded intervals—the area under the curve could be defined as the integral, and computed using approximation techniques on the region by polygons. However, as the need to consider more irregular functions arose—e.g., as a result of the limiting processes of mathematical analysis and the mathematical theory of probability—it became clear that more careful approximation techniques were needed to define a suitable integral. Also, we might wish to integrate on spaces more general than the real line. The Lebesgue integral provides the right abstractions needed to do this important job.The Lebesgue integral plays an important role in the branch of mathematics called real analysis, and in many other mathematical sciences fields. It is named after Henri Lebesgue (1875–1941), who introduced the integral (Lebesgue 1904). It is also a pivotal part of the axiomatic theory of probability.The term Lebesgue integration can mean either the general theory of integration of a function with respect to a general measure, as introduced by Lebesgue—or the specific case of integration of a function defined on a sub-domain of the real line with respect to Lebesgue measure.