1 Distributions or generalized functions.
... Notice that if L ∈ S ∗ then L ∈ D∗ . So if L ∈ S ∗ and L ∈ D0 the we will said that L is a tempered distribution. It is common to write S 0 for the set of tempered distributions. So a distribution is tempered if it can be also evaluated at functions of the Schwartz ...
... Notice that if L ∈ S ∗ then L ∈ D∗ . So if L ∈ S ∗ and L ∈ D0 the we will said that L is a tempered distribution. It is common to write S 0 for the set of tempered distributions. So a distribution is tempered if it can be also evaluated at functions of the Schwartz ...
Basic concept of differential and integral calculus
... In the first case we can solve y and rewrite the relationship as In second case it does not seem easy to solve for Y. When it is easy to express the relation as y=f(x) we say that y is given as an explicit function of x, otherwise it is an implicit function of x ...
... In the first case we can solve y and rewrite the relationship as In second case it does not seem easy to solve for Y. When it is easy to express the relation as y=f(x) we say that y is given as an explicit function of x, otherwise it is an implicit function of x ...
Muthuvel, R.
... Calculator: A graphing calculator is required and used for homework, quizzes, and tests. Note: TI-89 and TI-92 are not allowed. Bring your calculator to class every day. Course Description: In this course, we will cover topics including functions, graphs, data analysis and modeling of real world pro ...
... Calculator: A graphing calculator is required and used for homework, quizzes, and tests. Note: TI-89 and TI-92 are not allowed. Bring your calculator to class every day. Course Description: In this course, we will cover topics including functions, graphs, data analysis and modeling of real world pro ...
Muthuvel, R.
... Calculator: A graphing calculator is required and used for homework, quizzes, and tests. Note: TI-89 and TI-92 are not allowed. Bring your calculator to class every day. Course Description: In this course, we will cover topics including functions, graphs, data analysis and modeling of real world pro ...
... Calculator: A graphing calculator is required and used for homework, quizzes, and tests. Note: TI-89 and TI-92 are not allowed. Bring your calculator to class every day. Course Description: In this course, we will cover topics including functions, graphs, data analysis and modeling of real world pro ...
8.2 Integration by Parts
... Once we’ve used substitution to turn an integrand into a rational function, here is the strategy to use: 1. If you see immediately how to solve it, do so; otherwise go on: f (x) = ...
... Once we’ve used substitution to turn an integrand into a rational function, here is the strategy to use: 1. If you see immediately how to solve it, do so; otherwise go on: f (x) = ...
Muthuvel, R.
... Course Description: In this course, we will cover topics including functions, graphs, data analysis and modeling of real world problems, equations and inequalities, polynomial, rational functions, exponential and logarithmic functions, basic circular functions and their inverses, trigonometric ident ...
... Course Description: In this course, we will cover topics including functions, graphs, data analysis and modeling of real world problems, equations and inequalities, polynomial, rational functions, exponential and logarithmic functions, basic circular functions and their inverses, trigonometric ident ...
Section 3 Integral Equations
... where L is a linear ODE operator as in Section 1 (of at least second order), ρ (x) > 0 is continuous, g (x) is piecewise continuous and the unknown u (x) is subject to homogeneous boundary conditions at x = a, b. Suppose L has a known Green’s function under the given boundary conditions, G (x, y) sa ...
... where L is a linear ODE operator as in Section 1 (of at least second order), ρ (x) > 0 is continuous, g (x) is piecewise continuous and the unknown u (x) is subject to homogeneous boundary conditions at x = a, b. Suppose L has a known Green’s function under the given boundary conditions, G (x, y) sa ...
U-Substitution
... understand, make sure you ask me to walk you through it or clear up whatever is troubling you). The hard part about u-substitution is in fact the choice of this function u = f (x), and even knowing whether to write u = f (x) or x = g(u). Two basic guidelines are the following: Guideline. (Guideline ...
... understand, make sure you ask me to walk you through it or clear up whatever is troubling you). The hard part about u-substitution is in fact the choice of this function u = f (x), and even knowing whether to write u = f (x) or x = g(u). Two basic guidelines are the following: Guideline. (Guideline ...
Muthuvel, R.
... Calculator: A graphing calculator is required and used for homework, quizzes, and tests. Note: TI-89 and TI-92 are not allowed. Bring your calculator to class every day. Course Description: In this course, we will cover topics including functions, graphs, data analysis and modeling of real world pro ...
... Calculator: A graphing calculator is required and used for homework, quizzes, and tests. Note: TI-89 and TI-92 are not allowed. Bring your calculator to class every day. Course Description: In this course, we will cover topics including functions, graphs, data analysis and modeling of real world pro ...
4.1 Part 2 Particle Motion
... 4.3 Riemann Sums and Definite Integrals Definition of a Riemann Sum Let f be defined on the closed interval [a, b] and let be a partition of [a, b] given by a = x0 < x1 < x2 < . . . < xn - 1 < xn = b, where xi is the length of the ith subinterval. If ci is any point in the ith subinterval, then ...
... 4.3 Riemann Sums and Definite Integrals Definition of a Riemann Sum Let f be defined on the closed interval [a, b] and let be a partition of [a, b] given by a = x0 < x1 < x2 < . . . < xn - 1 < xn = b, where xi is the length of the ith subinterval. If ci is any point in the ith subinterval, then ...
ANTIDERIVATIVES AND AREAS AND THINGS 1. Integration is
... Now, we might want to figure out how much work we have done stretching this spring. High school physics tells us, “work = force × distance.” But in our case the force is changing with respect to distance! So, now what? The answer is to use an integral. Just like how, when the height of an area is ch ...
... Now, we might want to figure out how much work we have done stretching this spring. High school physics tells us, “work = force × distance.” But in our case the force is changing with respect to distance! So, now what? The answer is to use an integral. Just like how, when the height of an area is ch ...
Objective (Defn): something that one`s efforts or actions are intended
... problems. State the definition of antiderivative of f . State/find by sight the antiderivatives for x of simple functions. State and apply the rules for the general antiderivatives of constants times functions and sums or differences of functions. Find the general antiderivative of any given polynom ...
... problems. State the definition of antiderivative of f . State/find by sight the antiderivatives for x of simple functions. State and apply the rules for the general antiderivatives of constants times functions and sums or differences of functions. Find the general antiderivative of any given polynom ...
chapter1
... Important Rule: To determine the domain of a function, start with all real numbers and then eliminate anything that results in zero denominators or even roots of negative numbers. ...
... Important Rule: To determine the domain of a function, start with all real numbers and then eliminate anything that results in zero denominators or even roots of negative numbers. ...
Trig Unified Syllabus - North Allegheny School District
... Students planning to continue their study of mathematics in calculus, statistics or other disciplines, as well as those taking trigonometry as their final mathematics course, will benefit from the content in this class. Textbook Lial, Hornsby, Schneider, Trigonometry, Boston: Addison Wesley Company, ...
... Students planning to continue their study of mathematics in calculus, statistics or other disciplines, as well as those taking trigonometry as their final mathematics course, will benefit from the content in this class. Textbook Lial, Hornsby, Schneider, Trigonometry, Boston: Addison Wesley Company, ...
4.4 - korpisworld
... this would be the number. This is the same way your six-weeks average is calculated, although we are only adding up a discrete number of grades. To get around the little problem of adding up an infinite number of values and dividing by infinity, the MVT employs a little trick. If we could find the a ...
... this would be the number. This is the same way your six-weeks average is calculated, although we are only adding up a discrete number of grades. To get around the little problem of adding up an infinite number of values and dividing by infinity, the MVT employs a little trick. If we could find the a ...
math318hw1problems.pdf
... Notation 3.1. Recall that C 0 (Y ) denotes the collection of continuous functions Y → R. Let U ⊂ V ⊂ Y both be open subsets of Y . If f ∈ C 0 (V ) then f |U ∈ C 0 (U ). Denote f 7→ f |U by Res(U, V ) : C 0 (V ) → C 0 (U ). Let f : Y → Z be continuous. For every open V ⊂ Z and for every g ∈ C 0 (V ) ...
... Notation 3.1. Recall that C 0 (Y ) denotes the collection of continuous functions Y → R. Let U ⊂ V ⊂ Y both be open subsets of Y . If f ∈ C 0 (V ) then f |U ∈ C 0 (U ). Denote f 7→ f |U by Res(U, V ) : C 0 (V ) → C 0 (U ). Let f : Y → Z be continuous. For every open V ⊂ Z and for every g ∈ C 0 (V ) ...
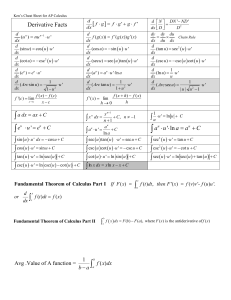
Ken`s Cheat Sheet 2014 Version 11 by 17
... For a limit to exist, the left and right hand limits must agree (be equal) V R r dx ...
... For a limit to exist, the left and right hand limits must agree (be equal) V R r dx ...
The Meaning of Integration
... he generalized the concept to much more general functions and provided an integrability condition. His condition was so weak that the mathematical community once thought it to be the most g~neral form of integration. But his theory, again was not powerful enough to handle many interesting and import ...
... he generalized the concept to much more general functions and provided an integrability condition. His condition was so weak that the mathematical community once thought it to be the most g~neral form of integration. But his theory, again was not powerful enough to handle many interesting and import ...
Muthuvel, R.
... Homework: Homework will be assigned for each section. These problems will not be collected for grading but used for discussion. Attendance: Attendance will be taken in each class. If absent, it is your responsibility to obtain the missed lecture notes and to do the assignment. Grading: ...
... Homework: Homework will be assigned for each section. These problems will not be collected for grading but used for discussion. Attendance: Attendance will be taken in each class. If absent, it is your responsibility to obtain the missed lecture notes and to do the assignment. Grading: ...
UNIVERSAL FUNCTIONS - Muskingum University
... function that can be used to describe all other functions. The Universal Function we will construct in this presentation will be a function whose translations (shift in their graph) will approximate any continuous function we can think of on a given closed bounded interval (i.e. U(x+t)f(x)). Think ...
... function that can be used to describe all other functions. The Universal Function we will construct in this presentation will be a function whose translations (shift in their graph) will approximate any continuous function we can think of on a given closed bounded interval (i.e. U(x+t)f(x)). Think ...
Computing Indefinite Integrals
... 7. Have each table come up with the antiderivative formulas for all the trig functions by reversing the derivative formulas. 8. Have them work on figuring out the antiderivative formulas for ex, ax, and ln(x). Explain how the ln(x) fills in the hole from before where x = -1. 9. Teach the students ho ...
... 7. Have each table come up with the antiderivative formulas for all the trig functions by reversing the derivative formulas. 8. Have them work on figuring out the antiderivative formulas for ex, ax, and ln(x). Explain how the ln(x) fills in the hole from before where x = -1. 9. Teach the students ho ...
Homework 8 - UC Davis Mathematics
... (a) Determine what well known function is obtained from sinh(x) + cosh(x). (b) Determine what well known function is obtained from cosh(x) − sinh(x). (c) Compute the derivatives of both sinh(x) and cosh(x). (d) What is the difference between the relationship of the derivatives of the hyperbolic trig ...
... (a) Determine what well known function is obtained from sinh(x) + cosh(x). (b) Determine what well known function is obtained from cosh(x) − sinh(x). (c) Compute the derivatives of both sinh(x) and cosh(x). (d) What is the difference between the relationship of the derivatives of the hyperbolic trig ...
Mathematics 4 Homework 2, solutions Prof. F. Brock 1. Let x 0 ∈ R
... 4. Let f : R → R be an increasing function. Show that f is Borel measurable. Solution : Let t ∈ R. Since f is increasing, the set {x : f (x) > t} is either ∅, R, a half line of the form (a, +∞), or a half line of the form [a, +∞), for some number a ∈ R. Since each of those sets is a Borel set, the a ...
... 4. Let f : R → R be an increasing function. Show that f is Borel measurable. Solution : Let t ∈ R. Since f is increasing, the set {x : f (x) > t} is either ∅, R, a half line of the form (a, +∞), or a half line of the form [a, +∞), for some number a ∈ R. Since each of those sets is a Borel set, the a ...
Honors Algebra 1 Syllabus
... Homework discussions will be scheduled after school as needed. AP Calculus AB study sessions will be held on 3 Saturdays prior to the AP Exam. Every student is expected to attend these Saturday sessions. Also, when we miss school due to a snow day, you will be expected to complete a snow packet assi ...
... Homework discussions will be scheduled after school as needed. AP Calculus AB study sessions will be held on 3 Saturdays prior to the AP Exam. Every student is expected to attend these Saturday sessions. Also, when we miss school due to a snow day, you will be expected to complete a snow packet assi ...
Double Integrals over Rectangular Regions
... function of y alone, which can then be integrated as a function of a single variable, thus producing what we call an iterated integral iterated integral ...
... function of y alone, which can then be integrated as a function of a single variable, thus producing what we call an iterated integral iterated integral ...
Lebesgue integration
In mathematics, the integral of a non-negative function can be regarded, in the simplest case, as the area between the graph of that function and the x-axis. The Lebesgue integral extends the integral to a larger class of functions. It also extends the domains on which these functions can be defined.Mathematicians had long understood that for non-negative functions with a smooth enough graph—such as continuous functions on closed bounded intervals—the area under the curve could be defined as the integral, and computed using approximation techniques on the region by polygons. However, as the need to consider more irregular functions arose—e.g., as a result of the limiting processes of mathematical analysis and the mathematical theory of probability—it became clear that more careful approximation techniques were needed to define a suitable integral. Also, we might wish to integrate on spaces more general than the real line. The Lebesgue integral provides the right abstractions needed to do this important job.The Lebesgue integral plays an important role in the branch of mathematics called real analysis, and in many other mathematical sciences fields. It is named after Henri Lebesgue (1875–1941), who introduced the integral (Lebesgue 1904). It is also a pivotal part of the axiomatic theory of probability.The term Lebesgue integration can mean either the general theory of integration of a function with respect to a general measure, as introduced by Lebesgue—or the specific case of integration of a function defined on a sub-domain of the real line with respect to Lebesgue measure.