Honors Geometry Test 1 Topics I. Definitions and undefined terms A
... Test 1 Topics I. Definitions and undefined terms A. Know which terms are the three undefined terms B. Definitions in Topic 1 up through “angle” and “vertex of an angle” on page 6 (You might especially want to look at opposite rays, space, vertex, and midpoint) II. Notation and naming A. Notation for ...
... Test 1 Topics I. Definitions and undefined terms A. Know which terms are the three undefined terms B. Definitions in Topic 1 up through “angle” and “vertex of an angle” on page 6 (You might especially want to look at opposite rays, space, vertex, and midpoint) II. Notation and naming A. Notation for ...
Going to the Pictures: Eigenvector as Fixed Point by Mervyn Stone
... (i) V is the p-dimensional vector space of variables (linear combinations of the names of the p observed variables) and E is the p-dimensional dual vector space of evaluators (linear functionals on V). (ii) The evaluation of variable v by evaluator e is given by the real-valued bilinear product [e, ...
... (i) V is the p-dimensional vector space of variables (linear combinations of the names of the p observed variables) and E is the p-dimensional dual vector space of evaluators (linear functionals on V). (ii) The evaluation of variable v by evaluator e is given by the real-valued bilinear product [e, ...
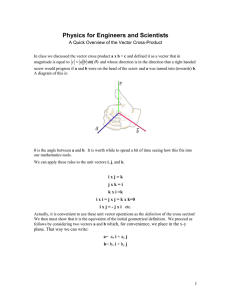
12. Vectors and the geometry of space 12.1. Three dimensional
... 12. Vectors and the geometry of space 12.1. Three dimensional coordinate systems. To locate a point in space, one needs to choose a point first as the reference, which is usually called the origin. Then, select three directed lines and labelled the x-axis, y-axis and z-axis. These three lines are nam ...
... 12. Vectors and the geometry of space 12.1. Three dimensional coordinate systems. To locate a point in space, one needs to choose a point first as the reference, which is usually called the origin. Then, select three directed lines and labelled the x-axis, y-axis and z-axis. These three lines are nam ...
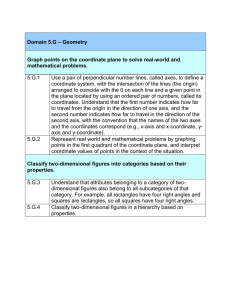
Grade Level/ Course (HS): 6 Grade Standard
... of a side joining points with the same first coordinate or the same second coordinate. Apply these techniques in the context of solving real-world and mathematical problems. ...
... of a side joining points with the same first coordinate or the same second coordinate. Apply these techniques in the context of solving real-world and mathematical problems. ...
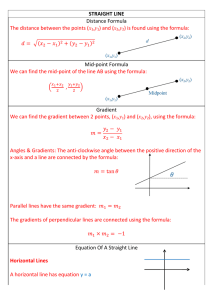
STRAIGHT LINE Distance Formula The distance between the points
... Vertical Lines A vertical line has equation x = b where b is the point that the line crosses the x-axis. ...
... Vertical Lines A vertical line has equation x = b where b is the point that the line crosses the x-axis. ...
Differential geometry of surfaces in Euclidean space
... indices, xA . Consider now an m-dimensional (m ≤ n) surface Σ embedded in Rn . It can be parameterized by a set of m “curvilinear” coordinates, denoted using Greek indices, y µ ; the surface is defined by giving the Euclidean coordinates xA as a function of the curvilinear ones, xA = xA (~y ). In th ...
... indices, xA . Consider now an m-dimensional (m ≤ n) surface Σ embedded in Rn . It can be parameterized by a set of m “curvilinear” coordinates, denoted using Greek indices, y µ ; the surface is defined by giving the Euclidean coordinates xA as a function of the curvilinear ones, xA = xA (~y ). In th ...
Solving Quadratic Equations by Completing the Square
... Introduction to Analytic Geometry Objective: Find the distance and midpoint between two points on a coordinate plane. Prove geometric relationships among points and lines using analytical methods. ...
... Introduction to Analytic Geometry Objective: Find the distance and midpoint between two points on a coordinate plane. Prove geometric relationships among points and lines using analytical methods. ...