Single Particle Tunneling in Strongly Driven Double Well Potentials
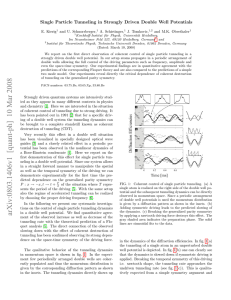
... The dependence of the tunneling splitting as a function of driving amplitude for fixed driving frequency ωd = 6kHz is shown in fig. 4(b). There we compare our experimental results with the Floquet and two mode theory. It is important to note that the potential parameters (V1 = 8.27Er , V2 = 2.68Er ) ...
... The dependence of the tunneling splitting as a function of driving amplitude for fixed driving frequency ωd = 6kHz is shown in fig. 4(b). There we compare our experimental results with the Floquet and two mode theory. It is important to note that the potential parameters (V1 = 8.27Er , V2 = 2.68Er ) ...
The Mean-Field Limit for the Dynamics of Large Particle
... One might think that the mean-field Schrödinger equation is a less universal object than its classical counterpart (the Vlasov equation) since there are so many variants of it — (1.6) and (1.7) for instance. In fact, (1.6) and (1.7) (and all the other variants of the mean-field Schrödinger equation) ...
... One might think that the mean-field Schrödinger equation is a less universal object than its classical counterpart (the Vlasov equation) since there are so many variants of it — (1.6) and (1.7) for instance. In fact, (1.6) and (1.7) (and all the other variants of the mean-field Schrödinger equation) ...
Preface, contents and abstracts
... 14.2 Anisotropy of γ . . . . . . . . . . . . . . . . . . . . 14.3 Curved Solid-Fluid Interfaces . . . . . . . . . . . . 14.3.1 Discontinuous Derivatives of γ . . . . . . . . 14.3.2 Inverted γ-plot . . . . . . . . . . . . . . . . 14.4 Faceting of a Large Planar Face . . . . . . . . . . . 14.5 Equilib ...
... 14.2 Anisotropy of γ . . . . . . . . . . . . . . . . . . . . 14.3 Curved Solid-Fluid Interfaces . . . . . . . . . . . . 14.3.1 Discontinuous Derivatives of γ . . . . . . . . 14.3.2 Inverted γ-plot . . . . . . . . . . . . . . . . 14.4 Faceting of a Large Planar Face . . . . . . . . . . . 14.5 Equilib ...
Quasiadiabatic description of nonlinear particle dynamics in typical
... action variable of the Hamiltonian dynamics and analogous to the the magnetic moment µ in the guiding center theory, was introduced by Speiser (1970). The important role played by Iz was first recognized by Sonnerup (1971). That single action variable is, naturally, not sufficient for a complete des ...
... action variable of the Hamiltonian dynamics and analogous to the the magnetic moment µ in the guiding center theory, was introduced by Speiser (1970). The important role played by Iz was first recognized by Sonnerup (1971). That single action variable is, naturally, not sufficient for a complete des ...
6.453 Quantum Optical Communication
... Continuous-Variable Teleportation: Xmtr Details ! Homodyne-Measurement Signal-to-Noise Ratios ...
... Continuous-Variable Teleportation: Xmtr Details ! Homodyne-Measurement Signal-to-Noise Ratios ...
No. 18 - Department of Mathematics
... related to the superconformal symmetry algebra psu(2, 2|4). We also discuss general features of classical integrability, higher charges and Lax pairs, using as a toy model the theory of the principal chiral field (14). Starting from section 4, we enter the core of the topic of this review, i.e. the ...
... related to the superconformal symmetry algebra psu(2, 2|4). We also discuss general features of classical integrability, higher charges and Lax pairs, using as a toy model the theory of the principal chiral field (14). Starting from section 4, we enter the core of the topic of this review, i.e. the ...
Lecture - Computer Science - University of Central Florida
... Polarization of Light Polarization is given by the electric field vector – Linearly polarized (vertical/horizontal) the tip of the electric field vector oscillates along any straight line in a plane perpendicular to the direction of propagation. – Circularly polarized (right- /left-hand) the ti ...
... Polarization of Light Polarization is given by the electric field vector – Linearly polarized (vertical/horizontal) the tip of the electric field vector oscillates along any straight line in a plane perpendicular to the direction of propagation. – Circularly polarized (right- /left-hand) the ti ...
QUANTUM ALGORITHMS FOR ELEMENT DISTINCTNESS∗ 1
... consider the situation where f : [N ] → Z and g : [M ] → Z are arbitrary. Our aim is to find a claw between f and g, if one exists. For now, let us assume N = M (in the body of the paper we treat the general case). The complexity measure we use is the number of comparisons between elements. That is ...
... consider the situation where f : [N ] → Z and g : [M ] → Z are arbitrary. Our aim is to find a claw between f and g, if one exists. For now, let us assume N = M (in the body of the paper we treat the general case). The complexity measure we use is the number of comparisons between elements. That is ...
Multi-Majoron Modes for Neutrinoless Double
... in class IB and IC are at present experimentally indistinguishable from those in class IIB. Similarly, classes ID and IE cannot be distinguished from class IIC. Interestingly, all of the models which had been considered previously, as well as most of the more recent proposals, fall into only a few ...
... in class IB and IC are at present experimentally indistinguishable from those in class IIB. Similarly, classes ID and IE cannot be distinguished from class IIC. Interestingly, all of the models which had been considered previously, as well as most of the more recent proposals, fall into only a few ...
A conformal field theory approach to the fractional quantum Hall
... states with non-abelian excitations, that can possibly occur in graphene. The derivation of these wave functions relies on an analysis using conformal field theory and group theory in analogy with an analysis done before for non-abelian SU(2) spin singlet states [1]. Structure of the thesis I wrote ...
... states with non-abelian excitations, that can possibly occur in graphene. The derivation of these wave functions relies on an analysis using conformal field theory and group theory in analogy with an analysis done before for non-abelian SU(2) spin singlet states [1]. Structure of the thesis I wrote ...
E. Waltersson, On the role of the electron
... Most theoretical studies have chosen a two dimensional harmonic oscillator potential as the confinement. An early motivation for this was the study by Kumar et al. [10] in 1990 who used self-consistent combined Hartree and Poisson solutions. They showed that the two-dimensional harmonic oscillator p ...
... Most theoretical studies have chosen a two dimensional harmonic oscillator potential as the confinement. An early motivation for this was the study by Kumar et al. [10] in 1990 who used self-consistent combined Hartree and Poisson solutions. They showed that the two-dimensional harmonic oscillator p ...























