Ch 6 Triangle Theorems
... draw a triangle and label the three angles, I would not get far with the proof. What I need to do is use all the information I have learned before and apply it to this theorem. Before this chapter we were working with parallel lines. While triangles are certainly not made up of parallel lines, I can ...
... draw a triangle and label the three angles, I would not get far with the proof. What I need to do is use all the information I have learned before and apply it to this theorem. Before this chapter we were working with parallel lines. While triangles are certainly not made up of parallel lines, I can ...
more work with complementary and supplementary angles 2016
... Two angles are complementary angles if the sum of the measures is __________. Two angles are supplementary angles if the sum of the measures is __________. All straight lines have a sum of _______________. All triangles have a sum of _____________. Vertical angles are opposite angles formed by the i ...
... Two angles are complementary angles if the sum of the measures is __________. Two angles are supplementary angles if the sum of the measures is __________. All straight lines have a sum of _______________. All triangles have a sum of _____________. Vertical angles are opposite angles formed by the i ...
2.6 Special Angles on Parallel Lines .pptx
... Are the two sets of angles congruent? Slide the top copy so that the transversal stays lined up. Trace the lines and the angles from your paper onto the patty paper. 6. What kinds of angles were formed? 7. Use your ruler to measure the distance between the two lines in three different places. Are ...
... Are the two sets of angles congruent? Slide the top copy so that the transversal stays lined up. Trace the lines and the angles from your paper onto the patty paper. 6. What kinds of angles were formed? 7. Use your ruler to measure the distance between the two lines in three different places. Are ...
Congruent Triangle Methods
... Angle-Angle-Side (AAS) Postulate • If two angles and a nonincluded side of one triangle are congruent to two angles and the corresponding nonincluded side of another triangle, then the two triangles are congruent. ...
... Angle-Angle-Side (AAS) Postulate • If two angles and a nonincluded side of one triangle are congruent to two angles and the corresponding nonincluded side of another triangle, then the two triangles are congruent. ...
1.2 Euclid`s Parallel Postulate - Department of Mathematical Sciences
... octahedron, cube, icosahedron, and dodecahedron [42]. For more information about Euclid and his environment, see the number theory chapter. Our focus will be specifically on the controversial parallel postulate in Book I and its ramifications, in particular the angle sum of triangles. Book I begins ...
... octahedron, cube, icosahedron, and dodecahedron [42]. For more information about Euclid and his environment, see the number theory chapter. Our focus will be specifically on the controversial parallel postulate in Book I and its ramifications, in particular the angle sum of triangles. Book I begins ...
4-6 Triangle Congruence: CPCTC Warm Up Lesson
... 4-6 Triangle Congruence: CPCTC Check It Out! Example 1 A landscape architect sets up the triangles shown in the figure to find the distance JK across a pond. What is JK? One angle pair is congruent, because they are vertical angles. Two pairs of sides are congruent, because their lengths are equal. ...
... 4-6 Triangle Congruence: CPCTC Check It Out! Example 1 A landscape architect sets up the triangles shown in the figure to find the distance JK across a pond. What is JK? One angle pair is congruent, because they are vertical angles. Two pairs of sides are congruent, because their lengths are equal. ...
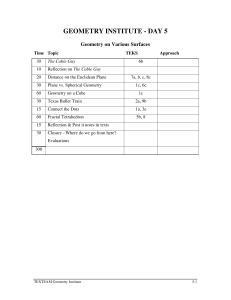
geometry institute - day 5
... discussion should follow the exploration of each postulate. Postulates Line Postulate: “For any two distinct points, there is one and only one line containing them”. Parallel Postulate: “Through a point not on a given line, one and only one line is parallel to the given line.” EXTENSIONS: ...
... discussion should follow the exploration of each postulate. Postulates Line Postulate: “For any two distinct points, there is one and only one line containing them”. Parallel Postulate: “Through a point not on a given line, one and only one line is parallel to the given line.” EXTENSIONS: ...
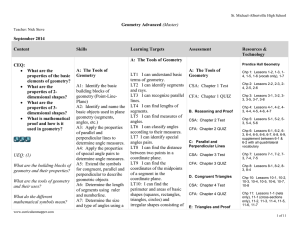
Geometry-Quarter-1-P..
... congruent; points on a perpendicular 1 day for assessment bisector of a line segment are exactly those equidistant from the segment’s endpoints. G.CO.10 Prove theorems about triangles. Theorems include: measures of interior angles of a triangle sum to 180°; base angles of isosceles triangles are con ...
... congruent; points on a perpendicular 1 day for assessment bisector of a line segment are exactly those equidistant from the segment’s endpoints. G.CO.10 Prove theorems about triangles. Theorems include: measures of interior angles of a triangle sum to 180°; base angles of isosceles triangles are con ...
Lesson 1.4 Polygons notes
... __________________________________________ – Two polygons that are identical in size and shape. They have corresponding sides and corresponding angles that are congruent. ...
... __________________________________________ – Two polygons that are identical in size and shape. They have corresponding sides and corresponding angles that are congruent. ...
Hyperbolic Geometry in the High School Geometry Classroom
... deduction, prove theorems, and critique arguments made by others”(2000, p. 308). ...
... deduction, prove theorems, and critique arguments made by others”(2000, p. 308). ...
Space
Space is the boundless three-dimensional extent in which objects and events have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum known as spacetime. The concept of space is considered to be of fundamental importance to an understanding of the physical universe. However, disagreement continues between philosophers over whether it is itself an entity, a relationship between entities, or part of a conceptual framework.Debates concerning the nature, essence and the mode of existence of space date back to antiquity; namely, to treatises like the Timaeus of Plato, or Socrates in his reflections on what the Greeks called khôra (i.e. ""space""), or in the Physics of Aristotle (Book IV, Delta) in the definition of topos (i.e. place), or in the later ""geometrical conception of place"" as ""space qua extension"" in the Discourse on Place (Qawl fi al-Makan) of the 11th-century Arab polymath Alhazen. Many of these classical philosophical questions were discussed in the Renaissance and then reformulated in the 17th century, particularly during the early development of classical mechanics. In Isaac Newton's view, space was absolute—in the sense that it existed permanently and independently of whether there was any matter in the space. Other natural philosophers, notably Gottfried Leibniz, thought instead that space was in fact a collection of relations between objects, given by their distance and direction from one another. In the 18th century, the philosopher and theologian George Berkeley attempted to refute the ""visibility of spatial depth"" in his Essay Towards a New Theory of Vision. Later, the metaphysician Immanuel Kant said that neither space nor time can be empirically perceived—they are elements of a systematic framework that humans use to structure all experiences. Kant referred to ""space"" in his Critique of Pure Reason as being a subjective ""pure a priori form of intuition"", hence it is an unavoidable contribution of our human faculties.In the 19th and 20th centuries mathematicians began to examine geometries that are not Euclidean, in which space can be said to be curved, rather than flat. According to Albert Einstein's theory of general relativity, space around gravitational fields deviates from Euclidean space. Experimental tests of general relativity have confirmed that non-Euclidean geometries provide a better model for the shape of space.