isometry
... 1. An isometry f is a translation if it is direct and is either the identity or has no fixed points. 2. An isometry f is a rotation if it is a direct isometry and is either the identity or there exists exactly one fixed point P (the center of rotation). 3. An isometry f is a reflection through the l ...
... 1. An isometry f is a translation if it is direct and is either the identity or has no fixed points. 2. An isometry f is a rotation if it is a direct isometry and is either the identity or there exists exactly one fixed point P (the center of rotation). 3. An isometry f is a reflection through the l ...
isometry - people.stfx.ca
... 1. An isometry f is a translation if it is direct and is either the identity or has no fixed points. 2. An isometry f is a rotation if it is a direct isometry and is either the identity or there exists exactly one fixed point P (the center of rotation). 3. An isometry f is a reflection through the l ...
... 1. An isometry f is a translation if it is direct and is either the identity or has no fixed points. 2. An isometry f is a rotation if it is a direct isometry and is either the identity or there exists exactly one fixed point P (the center of rotation). 3. An isometry f is a reflection through the l ...
Jeapordy - Chapter 9
... Given that a sector is 55% of a circle, how many degrees are in the central angle of the sector? ...
... Given that a sector is 55% of a circle, how many degrees are in the central angle of the sector? ...
3/16/13 Secondary Session Sallee Powerpoint
... • It appears that Euclid was correct when he said to King Ptolemy, “There is no royal road to geometry,” and rigid motions is not that road. • The tradeoffs are among understandability, rigor, and destroying belief in the value of proof. [Why should a high schooler see the need to prove that angle A ...
... • It appears that Euclid was correct when he said to King Ptolemy, “There is no royal road to geometry,” and rigid motions is not that road. • The tradeoffs are among understandability, rigor, and destroying belief in the value of proof. [Why should a high schooler see the need to prove that angle A ...
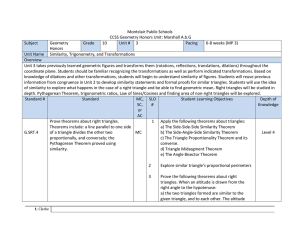
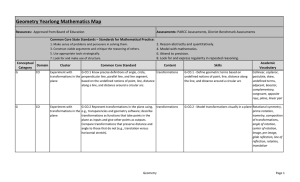
Geometry Unit Plan - Orange Public Schools
... perpendicular lines, parallel lines, and line segments. 5) G.CO.5: Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto ...
... perpendicular lines, parallel lines, and line segments. 5) G.CO.5: Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto ...
Poincaré`s Disk Model for Hyperbolic Geometry
... / AB, then we can draw at least two lines through D that do not intersect AB. Call these two lines through D lines ℓ1 and ℓ2 . Notice←→ now how two of←→ our previous results do not hold, as we remarked earlier. We have that AB and ℓ1 and AB and ℓ2 are parallel, but ℓ1 and ℓ2 are not parallel. Note a ...
... / AB, then we can draw at least two lines through D that do not intersect AB. Call these two lines through D lines ℓ1 and ℓ2 . Notice←→ now how two of←→ our previous results do not hold, as we remarked earlier. We have that AB and ℓ1 and AB and ℓ2 are parallel, but ℓ1 and ℓ2 are not parallel. Note a ...
1 Lecture 7 THE POINCARÉ DISK MODEL OF HYPERBOLIC
... 7.8. Hyperbolic geometry and the physical world In his famous book Science et Hypothèse, Henri Poincaré describes the physics of a small “universe” and the physical theories that its inhabitants would create. The universe considered by Poincaré is Euclidean, plane (twodimensional), has the form o ...
... 7.8. Hyperbolic geometry and the physical world In his famous book Science et Hypothèse, Henri Poincaré describes the physics of a small “universe” and the physical theories that its inhabitants would create. The universe considered by Poincaré is Euclidean, plane (twodimensional), has the form o ...
Mathematical Arguments and Triangle Geometry
... Line = circular arc, meets fundamental circle ...
... Line = circular arc, meets fundamental circle ...
Formal Geometry Semester 1 EOC Blueprint Common Core
... G.CO.9 Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant ...
... G.CO.9 Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant ...
THE UNIFORMIZATION THEOREM AND UNIVERSAL COVERS
... contract any loop to a single point all the while keeping it within our space; in even simpler terms, a simply connected space is one without any holes. To show that the complex plane, the open unit disk, and the Riemann sphere are simply-connected, we will show how to contract any loop to a single ...
... contract any loop to a single point all the while keeping it within our space; in even simpler terms, a simply connected space is one without any holes. To show that the complex plane, the open unit disk, and the Riemann sphere are simply-connected, we will show how to contract any loop to a single ...